2024年陕西省咸阳市九年级中考一模数学试题（原卷版+解析版）

这是一份2024年陕西省咸阳市九年级中考一模数学试题（原卷版+解析版），文件包含2024年陕西省咸阳市九年级中考一模数学试题原卷版docx、2024年陕西省咸阳市九年级中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
1. 计算的结果等于（ ）
A. 6B. C. 12D.
【答案】D
【解析】
【分析】本题主要考查了有理数的减法．根据有理数的减法运算法则计算，即可求解．
【详解】解：．
故选：D
2. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A B. C. D.
【答案】C
【解析】
【分析】本题考查了中心对称图形与轴对称图形的识别；根据中心对称图形和轴对称图形的概念逐项分析即可，轴对称图形：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．中心对称图形：在平面内，把一个图形绕着某个点旋转，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．
【详解】解：A选项不是轴对称图形，是中心对称图形，不符合题意；
B选项是轴对称图形，不是中心对称图形，不符合题意；
C选项既是轴对称图形，又是中心对称图形，符合题意；
D选项是轴对称图形，不是中心对称图形，不符合题意．
故选：C．
3. 如图，把一根铁丝折成图示形状后，，若，，则∠B等于（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了平行线的性质，三角形外角的性质．根据三角形外角的性质求出，再由平行线的性质表示出即可得出答案．
【详解】解：∵，，
∴．
∵，
∴．
故选D．
4. 已知单项式与的积为，那么、的值为（ ）
A. ，B. ，
C. ，D. ，
【答案】B
【解析】
【分析】按照单项式乘单项式计算单项式与的积，再根据单项式与的积为，即可求得答案．
【详解】解：∵，单项式与的积为，
∴，，
故选：B
【点睛】此题考查了单项式的乘法运算，熟练掌握运算法则是解题的关键．
5. 下列图象中，可以表示一次函数与正比例函数（k，b为常数，且）的图象不可能的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查正比例函数的图象、一次函数的图象，根据正比例函数的性质和一次函数的图象，可以得到的正负和、的正负，然后即可判断哪个选项符合题意．
【详解】A、由一次函数的图象可知，，由正比例函数的图象可知，故选项A不可能，符合题意；
B、由一次函数的图象可知，，由正比例函数的图象可知，故选项B可能，不符合题意；
C、由一次函数的图象可知，，由正比例函数的图象可知，故选项C可能，不符合题意；
D、由一次函数的图象可知，，由正比例函数的图象可知，故选项D可能，不符合题意；
故选：A．
6. 如图，在四边形中，，，，、、分别是、、的中点，若，则的周长是（ ）
A. 10B. 12C. 16D. 18
【答案】B
【解析】
【分析】本题考查的是三角形的中位线定理，等边三角形的判定与性质，平行线的性质；利用三角形的中位线先证明，同理求解，再证明为等边三角形，从而可得结论．
【详解】解：∵、分别是的中点，
∴是的中位线，
∴，，
∴，
同理可得，是的中位线，
∴，，
∴，
∴，
又∵，
∴为等边三角形，
∴，
∴的周长是12，
故选：B．
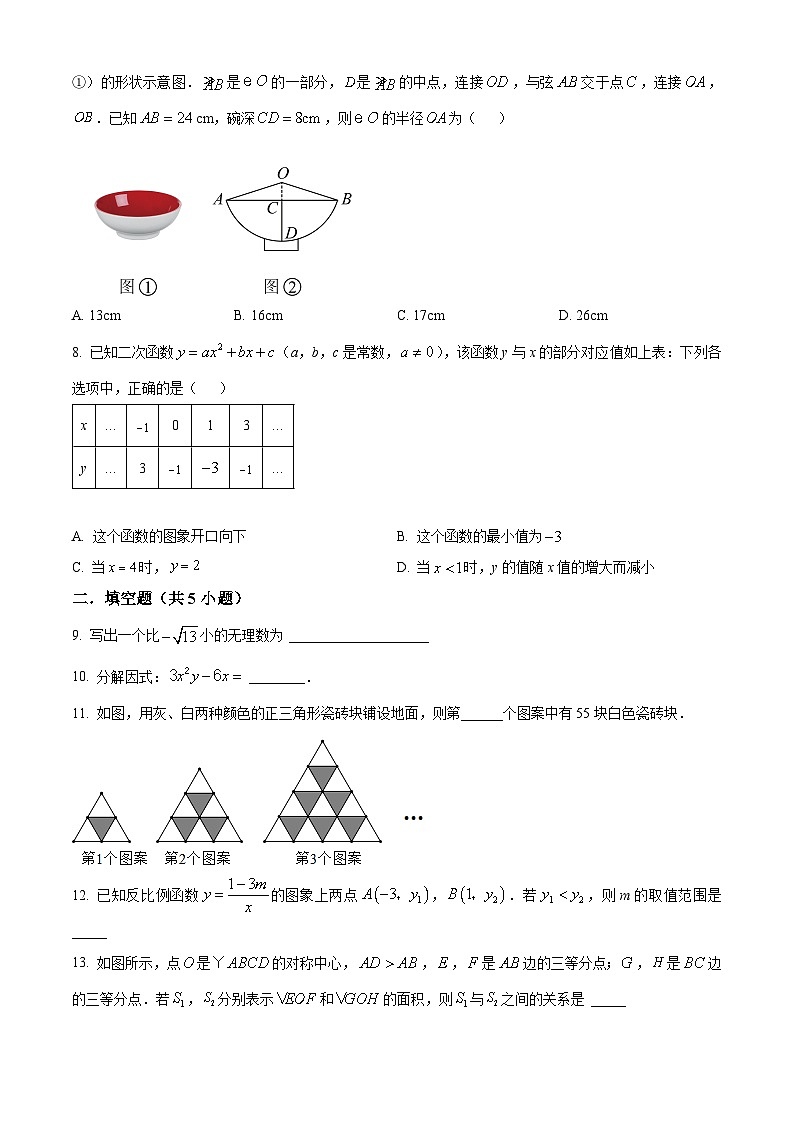
7. 陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一．图②是从正面看到的一个“老碗”（ 图①）的形状示意图．是的一部分，是的中点，连接，与弦交于点，连接，．已知cm，碗深，则的半径为（ ）

A. 13cmB. 16cmC. 17cmD. 26cm
【答案】A
【解析】
【分析】首先利用垂径定理的推论得出，，再设的半径为，则．在中根据勾股定理列出方程，求出即可．
【详解】解：是的一部分，是的中点，，
，．
设的半径为，则．
在中，，
，
，
，
即的半径为．
故选：A．
【点睛】本题考查了垂径定理、勾股定理的应用，设的半径为，列出关于的方程是解题的关键．
8. 已知二次函数（a，b，c是常数，），该函数y与x的部分对应值如上表：下列各选项中，正确的是（ ）
A. 这个函数的图象开口向下B. 这个函数的最小值为
C. 当时，D. 当时，y的值随x值的增大而减小
【答案】D
【解析】
【分析】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系．
通过待定系数法求出函数解析式，从而可得抛物线开口方向及对称轴，进而求解．
【详解】将代入得：
解得：
∴抛物线开口向上，选项A错误，
将代入得
∴C错误，
∵抛物线经过，
∴抛物线对称轴为直线，
将代入得
∴函数最小值为，选项B错误，
∵抛物线对称轴为直线，
∴时，随增大而减小，选项D正确．
故选：D．
二．填空题（共5小题）
9. 写出一个比小的无理数为 ____________________
【答案】（答案不唯一）
【解析】
【分析】本题考查了无理数的定义，实数的大小比较等，初中阶段学习的无理数有三种形式：①开方开不尽的数，②无限不循环小数，③含有的数等，熟练掌握相关知识是解题的关键．根据无理数的定义，找一个比小的无理数即可．
【详解】解∶ 比小的无理数为，
故答案为∶ （答案不唯一）．
10. 分解因式： ________．
【答案】
【解析】
【分析】本题主要考查了因式分解，解题的关键是掌握因式分解的方法．利用提公因式法即可求解．
【详解】解：
故答案为：．
11. 如图，用灰、白两种颜色的正三角形瓷砖块铺设地面，则第______个图案中有55块白色瓷砖块．
【答案】9
【解析】
【分析】根据图形的变化寻找规律即可求解．
【详解】解：观察图形的变化可知：
第1个图中白色瓷砖1+2=3块；
第2个图中白色瓷砖1+2+3=6块；
第3个图中白色瓷砖1+2+3+4=10块；
…
发现规律，
第n个图中白色瓷砖（1+2+3++1）块；
1+2+3++1=55，
解得n=9．
故答案为：9．
【点睛】本题考查了规律型-图形的变化类，解决本题的关键是观察图形的变化寻找规律并用代数式表示．
12. 已知反比例函数的图象上两点，．若，则m的取值范围是 _____
【答案】
【解析】
【分析】本题考查了反比例函数的性质， 根据反比例函数的性质，可以得到关于m的不等式，从而可以求得m的取值范围．
【详解】解∶∵反比例函数的图象上两点，，，
∴，
解得，
故答案为∶ ．
13. 如图所示，点是的对称中心，，，是边的三等分点；，是边的三等分点．若，分别表示和的面积，则与之间的关系是 _____
【答案】 # #
【解析】
【分析】本题考查了平行四边形的性质，根据三等分点可得，；再结合点是的对称中心可得 ，即可求解．
【详解】解：连接，则必过点，如图所示：
∵，是边的三等分点，
∴，
∵G，H是边的三等分点，
∴，
∵点O是的对称中心，
∴
∴
故答案为：
二．解答题（共5小题）
14. 解不等式：．
【答案】
【解析】
【分析】利用去分母，合并以及不等式的基本性质解一元一次不等式方法计算即可．
【详解】解：
去分母，得
移项、合并同类项，得
∴．
【点睛】本题主要考查一元一次不等式的解法，熟练掌握不等式的基本性质是解决本题的关键．
15 计算：
【答案】
【解析】
【分析】根据立方根、负整数指数幂及二次根式的运算可进行求解．
【详解】解：原式
．
【点睛】本题主要考查立方根、负整数指数幂及二次根式的运算，熟练掌握立方根、负整数指数幂及二次根式的运算是解题的关键．
16. 计算： ．
【答案】
【解析】
【分析】本题考查了分式的混合运算，正确理解运算顺序是关键．
首先计算括号内的式子，把除法转化成乘法，然后进行约分即可求解．
【详解】解：
=
=
=
17. 如图，为的一条弦，连接、，请在上作点C使得为以为底边的等腰三角形．（尺规作图，保留作图痕迹，不写作法）
【答案】图见详解
【解析】
【分析】分别以点A、B为圆心，大于AB长的一半为半径画弧，交于两点，连接这两点，交于点C，则问题可求解．
【详解】解：如图所示：
【点睛】本题主要考查垂径定理及等腰三角形的性质，熟练掌握垂径定理是解题的关键．
18. 如图，，平分，点为中点，求证：．

【答案】见解析
【解析】
【分析】延长，交于点，根据证明与全等，进而利用全等三角形的性质解答即可．
【详解】证明：延长，交于点，

，
，
点是的中点，
，
在与中，
，
，
，
平分，
，
，
，
，
，
．
【点睛】此题考查全等三角形的判定和性质，关键是根据证明．
19. 2023年10月26日，搭载三名航天员汤洪波、唐胜杰、江新林的神舟十七号载人飞船发射成功，三名航天员顺利进驻我国空间站．根据安排此次航天员乘组将进行出舱开展科学实验，每名航天员出舱的机会均等．
（1）首次将安排1名航天员出舱，则航天员汤洪波被选中出舱的概率是___________；
（2）若第2次安排两名航天员出舱，用列表或画树状图的方法求航天员汤洪波和唐胜杰同时出舱的概率．
【答案】（1）
（2）
【解析】
【分析】本题主要考查了用列表法或树状图法求概率，根据题意，列出图表或树状图，利用概率公式计算概率即可．
（1）直接根据概率计算即可．
（2）根据列表法得出所有等可能情况，找出符合条件的情况数，利用概率公式即可求解．
【小问1详解】
解：从三名航天员中安排1名航天员出舱，则航天员汤洪波被选中出舱的概率是
【小问2详解】
根据题意，列表如下：
由上表得共有6种可能结果，航天员汤洪波和唐胜杰同时出舱的情况有2种，故
航天员汤洪波和唐胜杰同时出舱的概率为．
20. 小明用的练习本可以到甲商店购买，也可以到乙商店购买．已知两店的标价都是每本1元，甲商店的优惠条件是买10本以上，从第11本开始按标价的7折卖；乙商店的优惠条件是购买10本以上，每本按标价的8折卖．
（1）小明要买20本练习本，到哪个商店较省钱？
（2）小明要买10本以上练习本，买多少本时到两个商店付的钱一样多？
（3）小明现有32元钱，最多可买多少本练习本？
【答案】（1）到乙商店较省钱；（2）买30本；（3）最多可买41本练习本．
【解析】
【分析】（1）分别按照甲商店与乙商店给的优惠活动，计算出费用，哪个商店的费用更低，即更省钱，即可解决；
（2）可设买x本时到两个商店付的钱一样多，分别用x表示到甲商店购买的钱与到乙商店购买的钱，令其相等，解出x，即可解决本题；
（3）设可买y本练习本，分别算出到甲商店能买多少本，到乙商店能买多少本，取更多的即可解决．
【详解】解：（1）∵甲商店：(元)；乙商店：(元)．
又∵17＞16，
∴小明要买20本练习本时，到乙商店较省钱．
（2）设买x本时到两个商店付的钱一样多．
依题意，得，解得．
∴买30本时到两个商店付的钱一样多．
（3）设可买y本练习本．
在甲商店购买：．
解得．
∵y为正整数，∴在甲商店最多可购买41本练习本．
在乙商店购买：．
解得．∴在乙商店最多可购买40本练习本．
∵41＞40，∴最多可买41本练习本．
【点睛】本题主要考查了一元一次方程的实际应用，能够找出等量关系，列出方程是解决本题的关键．
21. 西安丰庆公园是现代生态景观与历史文化景观融为一体的皇家园林，公园中的怡心阁是园内的最高建筑．某数学活动小组想测量怡心阁的高度，借助测角仪与标杆测量怡心阁的高度：小明沿后退到F恰好看到标杆顶端C与怡心阁的顶端A重合，小明继续后退到点H用测角仪测得怡心阁顶端A的仰角为，已知小明的眼睛到地面的距离，，，，B、D、F、H在同一直线上，和均与垂直，测量示意图如图所示，请你根据以上测量信息，求怡心阁的高度．（参考数据：，，，结果精确到1米）
【答案】米
【解析】
【分析】延长分别交，于点，证明，根据相似三角形的性质求得，在中，根据求得的值，进而求得的长．
【详解】解：如图所示，延长分别交，于点，
依题意，，
∴，
∵，
∴，
∴，
设，
则，
∴，
在中，，
解得：，
∴米．
【点睛】本题考查了相似三角形的性质，解直角三角形的应用，掌握相似三角形的性质以及三角函数的应用是解题的关键．
22. 一泳池清洗完毕后，用甲，乙两台不同的水泵同时向泳池内注水，一段时间后，甲水泵因故障停了一段时间，乙水泵继续注水，甲水泵维修完继续按原来的速度注水，从开始注水到结束共用90分钟，水池内水的总量为（）与放水时间（分钟）之间的函数图象如图所示．
（1）甲水泵每分钟注水 ；
（2）求甲水泵维修完后，与之间的函数关系式；
（3）求泳池中的水量是所需水量的一半时，注水的时间是多少分钟；
（4）在整个注水过程中，哪台水泵注水较多，多多少立方米？
【答案】（1）8； （2）；
（3）；
（4）甲台水泵注水较多，立方米．
【解析】
【分析】本题考查了一次函数的应用，利用待定系数法求一次函数的解析式，然后根据一次函数解决实际问题，正确求出一次函数的解析式，熟悉工作总量，工作效率，工作时间三者之间的关系是解题的关键．
（1）结合图像，计算出甲和乙的工作效率和，以及乙的工作效率，从而得到甲的工作效率；
（2）先求出值，再利用待定系数法解答即可；
（3）利用（2）中的表达式计算即可；
（4）分别算出甲和乙的注水量，再进行比较．
【小问1详解】
甲水泵的注水速度为：（分）
【小问2详解】
，
设，
代入，，
，
得到，
；
【小问3详解】
由题意可知，
注水时间为分钟；
【小问4详解】
甲水泵注水量为，
乙水泵的注水量为，
，（）
甲水泵注水较多，多20．
23. 珍爱生命，安全出行，关注安全就是关注生命．为了了解同学们对防溺水知识的了解程度，增强同学们的安全意识，某校在七年级随机抽取了部分学生进行了相关知识的测试，现把调查结果分成A，B，C，D四组，绘制成如图不完整的统计图：
根据以上信息，解答下列问题：
（1）本次调查总人数为 ； ；并补全条形统计图；
（2）这次测试成绩的中位数落在 组；
（3）求本次测试成绩的平均数．
【答案】（1）200；36；见解析
（2）C （3）分
【解析】
【分析】本题主要考查了扇形统计图和条形统计图的信息关联，求一组数据的平均数、中位数，解题的关键是数形结合，熟练掌握扇形统计图和条形统计图的特点．
（1）根据B组的人数和所占的百分比进行求解即可得出本次调查总人数，求出C组所占的百分比即可求出m的值；求出D组的人数，然后补全条形统计图即可；
（2）根据中位数的定义进行判断即可；
（3）总分数除以总人数即可求出平均数．
小问1详解】
解：本次调查的总人数为：（人），
∵，
∴，
D组人数为：（人），补全条形统计图，如图所示：
【小问2详解】
解：∵A组有24人，B组有48人，C组有72人，D组有60人，
∴将200人的成绩从小到大进行排序，排在第100和101的一定在C组，
∴这次测试成绩的中位数落在C组；
【小问3详解】
解：本次测试成绩的平均数为：
（分）．
24. 如图，为的直径，点C是弧的中点，点D在圆O上，点E在的延长线上，且．
（1）求证：DE是的切线；
（2）连接，若，，求的长．
【答案】（1）见解析 （2）9
【解析】
【分析】（1）连接，，利用等弧所对圆心角相等以及平角定义求出，进而求出，利用等边对等角可得出，，结合对顶角的性质可求出，利用切线的判定即可得证；
（2）过D作于H，利用同角的三角函数性质求出，设，，半径为r，在中，利用勾股定理求出 ，进而求出，在中，利用正切定义求出，在中，利用正切定义求出，即可求解．
【小问1详解】
解：连接，，
∵点C是弧中点，
∴，
∴，
又，
∴，
∴，
∵，，
∴，，
又，
∴，即，
∴，
又是的半径，
∴是的切线；
【小问2详解】
解：过D作于H，
∵，
∴，
∴，
设，，半径为r，
则，
在中，，
∴，
解得 ，
∴，
∴，
∴，即，
∴，
∴．
【点睛】本题考查了圆周角定理，等腰三角形的性质，切线的性质与判定，勾股定理，锐角三角函数等知识，明确题意，添加合适辅助线，构造直角三角形求解是解题的关键．
25. 如图，在平面直角坐标系中，直线的函数表达式为（，为常数），点、分别在轴和轴上，且，点关于轴的对称点为，点关于轴的对称点为，以点为顶点的抛物线经过点．
（1）求点的坐标；
（2）求抛物线的解析式；
（3）在（2）中抛物线的对称轴上有一点，且以点、、为顶点的三角形与相似，求出所有满足条件的点的坐标．
【答案】（1），
（2）抛物线的解析式为
（3）满足条件的点的坐标为或或或
【解析】
【分析】本题考查二次函数综合应用，对称变换，三角形相似的判定与性质；
（1）在中，令得可得，又，即有；
（2）根据点关于轴的对称点为，点关于轴的对称点为，得，，设抛物线的解析式为，将点代入得可求出，故抛物线的解析式为；
（3）因点在抛物线的对称轴上，即在轴上，故，而，，所有要使以点、、为顶点的三角形与相似，只需或，设点的坐标为，①当 时，，有，可得，；②当 时，，有，可得，．
【小问1详解】
解：在中，令得：，
解得，
，
，
，
，
；
【小问2详解】
解：点关于轴对称点为，点关于轴的对称点为，
由（1）知，，
，，
由以点为顶点的抛物线经过点，设抛物线的解析式为，
将点代入得：，
解得，
抛物线的解析式为；
【小问3详解】
解：如图：
点在抛物线 的对称轴上，即在轴上，
，
，，
要使以点、、为顶点的三角形与相似，只需或，
设点的坐标为，
①当时，，
，
，
，；
②当时，，
，
，
，，
综上所述，满足条件的点的坐标为或或或．
26. 问题探究
（1）如图①，在正方形ABCD内，请画出使∠BPC＝90°的所有点P；
（2）如图②，已知矩形ABCD，AB＝9，BC＝10，在矩形ABCD内画出使∠BPC＝60°的所有点P，并求出△APD面积的最小值；
（3）随着社会发展，农业观光园走进了我们的生活．某农业观光园的平面示意图如图3所示的四边形ABCD，其中∠A＝120°，∠B＝∠C＝90°，AB＝km，BC＝6km，观光园的设计者想在园中找一点P，使得点P与点A、B、C、D所连接的线段将整个观光园分成四个区域，用来进行不同的设计与规划，从实用和美观的角度他们还要求在△BPC的区域内∠BPC＝120°，且△APD的区域面积最小，试问在四边形ABCD内是否存在这样的点P，使得∠BPC＝120°，且△APD面积最小？若存在，请你在图中画出点P点的位置，并求出△APD的最小面积．若不存在，说明理由．

【答案】（1）详见解析；（2）图详见解析，45﹣25；（3）存在，图详见解析，9﹣12．．
【解析】
【分析】（1）如图1中，以BC为直径作⊙O，点P的轨迹是（不包括B，C）．
（2）如图2中，以BC为边向上作等边三角形△BCP，作△BCP的外接圆，交AB于E，交CD于F，点P轨迹是（不包括E，F），当点P是的中点时，△ADP的面积最小．
（3）如图3中，以BC为边向下作等边三角形△BCE，作△BCE的外接圆，点P轨迹是（不包括B，C），作OJ⊥BC于J，交AD于K，作AT⊥OK于T．延长OP交AD于H，当OH⊥AD时，PH的值最小，此时△PAD的面积最小．
【详解】解：（1）如图1中，以BC为直径作⊙O，点P的轨迹是（不包括B，C）．

（2）如图2中，以BC为边向上作等边三角形△BCP，作△BCP的外接圆，交AB于E，交CD于F，点P轨迹是（不包括E，F），

当点P是的中点时，△ADP的面积最小．
此时S△APD＝×10×（9﹣5）＝45﹣25．
（3）如图3中，以BC为边向下作等边三角形△BCE，作△BCE的外接圆，点P轨迹是（不包括B，C），

作OJ⊥BC于J，交AD于K，作AT⊥OK于T．延长OP交AD于H，当OH⊥AD时，PH的值最小，此时△PAD的面积最小．
由题意BJ＝JC＝3，OJ＝，
∵四边形ABJT是矩形，
∴∠BAT＝90°，AT＝BJ＝3，AB＝TJ＝，
∵∠DAB＝120°，
∴∠KAT＝30°，
∴KT＝，AK＝2，
∴OK＝OJ+JT+TK＝3，
∵∠OKH＝60°，
∴OH＝OK•sin60°＝，
∴PH＝OH﹣OP＝﹣2，
∵AB∥JK∥CD，BJ＝CJ，
∴AK＝KD＝2，
∴AD＝4，
∴△PAD的面积的最小值＝×（﹣2）＝9﹣12．
【点睛】本题属于四边形综合题，考查了正方形的性质，矩形的性质，等边三角形的性质，三角形的外接圆，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造辅助圆解决问题，属于中考压轴题．x
…
0
1
3
…
y
…
3
…
汤洪波
唐胜杰
江新林
汤洪波
—
汤洪波，唐胜杰
汤洪波，江新林
唐胜杰
唐胜杰，汤洪波
—
唐胜杰，江新林
江新林
江新林，汤洪波
江新林，唐胜杰
—
组别
分数/分
各组总分/分
A
1320
B
3650
C
6930
D
5600