广东省梅州市大埔县虎山中学2023-2024学年高一下学期4月期中教学质量检测数学试题（原卷版+解析版）

这是一份广东省梅州市大埔县虎山中学2023-2024学年高一下学期4月期中教学质量检测数学试题（原卷版+解析版），文件包含广东省梅州市大埔县虎山中学2023-2024学年高一下学期4月期中教学质量检测数学试题原卷版docx、广东省梅州市大埔县虎山中学2023-2024学年高一下学期4月期中教学质量检测数学试题解析版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
（考试时间：120分钟 试卷满分：150分 命题人：高一备课组）
一、单项选择题：（本题共8小题，每小题5分，共40分）
1. 如果复数是纯虚数，则实数的值为（ ）
A. 2或3B. 0或3C. 0D. 2
2. 已知是第四象限角，且，则（ ）
A. B. C. D. 7
3. 已知平面向量，，若，则（ ）
A. B. 0C. D.
4. 已知，则与夹角的余弦值为（ ）
A B. C. 0D. 1
5. 下列函数中，以为周期且在上单调递增的是（ ）
A. B.
C. D.
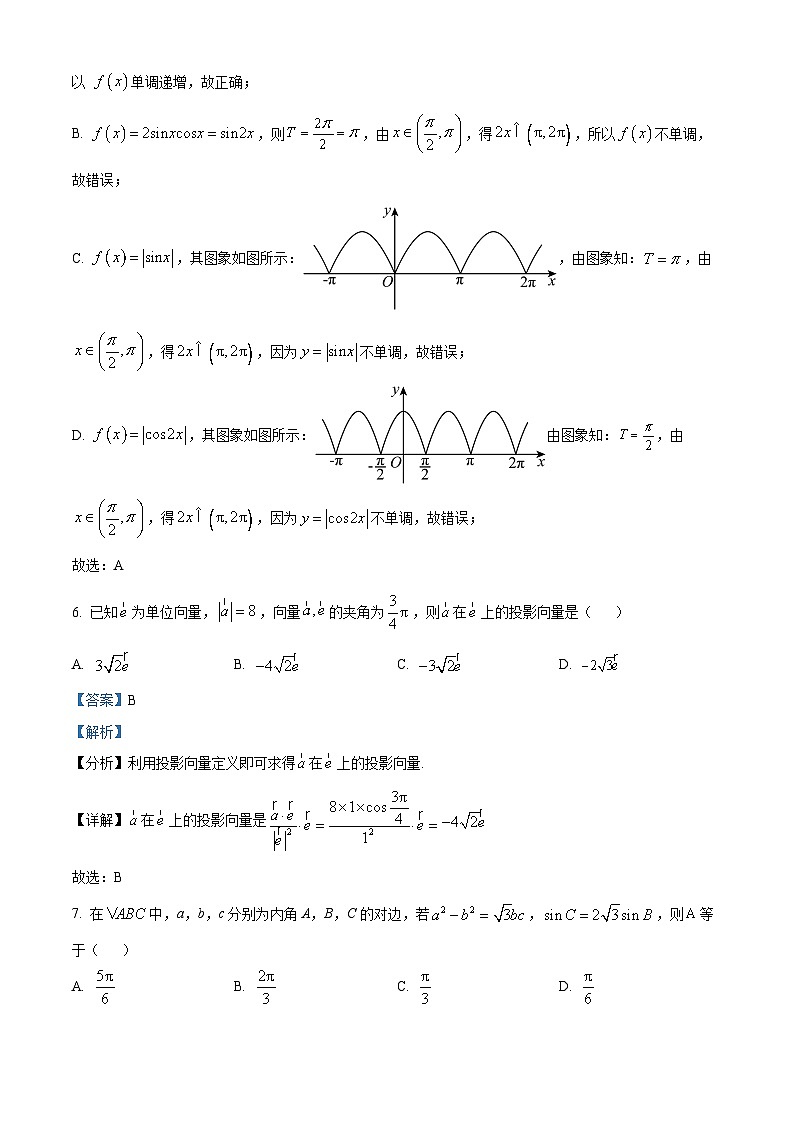
6. 已知为单位向量，，向量的夹角为，则在上的投影向量是（ ）
A. B. C. D.
7. 在中，a，b，c分别为内角A，B，C的对边，若，，则等于（ ）
A. B. C. D.
8. 中，已知，且，则是
A. 三边互不相等的三角形B. 等边三角形
C. 等腰直角三角形D. 顶角为钝角等腰三角形
二、多项选择题：（本题共3小题，每小题6分，共18分，全选对得6分，有选错得0分）
9. 下列三角式中，值为1的是（ ）
A. B.
C. D.
10. 下列说法中错误为（ ）
A. 已知，且与夹角为锐角，则λ的取值范围是
B. 已知，不能作为平面内所有向量的一组基底
C. 若与平行，则在方向上的投影数量为
D. 若非零，满足，则与的夹角是60°
11. 已知函数，（）的部分图象如图所示，将函数的图象上所有点的横坐标变为原来的，纵坐标不变，再将所得函数图象向右平移个单位长度，得到函数的图象，则下列关于函数的说法正确的是（ ）
A. 的最小正周期为
B. 在区间上单调递增
C. 的图象关于直线对称
D. 的图象关于点成中心对称
三、填空题：（本题共3小题，每小题5分，共15分）
12. 复数____.
13. 如图所示，直观图四边形是一个底角为，腰和上底均为1的等腰梯形，那么原平面图形的面积是______．
14. 在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式，利用三角形的三条边长求三角形面积，若三角形的三边长为，，，其面积，这里．已知在中，，，则面积的最大值为__________．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15. 已知函数，记集合为定义域，．
（1）化简集合，，并求；
（2）判断函数的奇偶性；
（3）当，求函数的值域．
16. 在锐角△ABC中，角A，B，C所对的边分别为a，b，c，已知，且．
（1）求证：；
（2）若的平分线交AC于D，且，求线段BD的长度的取值范围．
17. 已知坐标平面内，，，，．
（1）当，，三点共线时，求的值；
（2）当取最小值时，求的坐标，并求的值．
18. 已知的内角A，B，C的对边为a，b，c，且．
（1）求；
（2）若的面积为；
①已知E为BC的中点，求底边BC上中线AE长的最小值；
②求内角A的角平分线AD长的最大值．
19. 已知为坐标原点，对于函数，称向量为函数的伴随向量，同时称函数为向量的伴随函数.
（1）设函数，试求的伴随向量；
（2）记向量伴随函数为，求当且时，的值；
（3）已知将（2）中的函数的图象上各点的横坐标缩短到原来的倍，再把整个图象向右平移个单位长度得到的图象，若存在，使成立，求a的取值范围.