江西省南昌市南昌县2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份江西省南昌市南昌县2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含江西省南昌市南昌县2023-2024学年七年级下学期期中数学试题原卷版docx、江西省南昌市南昌县2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

1. 下列各图中,∠1与∠2是对顶角的是( )
A B. C. D.
【答案】C
【解析】
【分析】依据对角的定义进行判断即可．
【详解】解：∵互为对顶角的两个角的两边互为反向延长线，
∴A中∠1和∠2是邻补角，C中的∠1和∠2是对顶角．
故选C．
【点睛】本题主要考查的是邻补角、对顶角的定义，熟练掌握相关概念是解题的关键．
2. 的平方根是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】依据平方根的定义、算术平方根的定义进行解答即可．
【详解】解：∵，
∴的平方根是；
故选D.
【点睛】本题主要考查的是算术平方根、平方根的定义，熟练掌握相关概念是解题的关键．
3. 在下列所给出坐标的点中，在第二象限的是
A. （2，3）B. （﹣2，3）C. （﹣2，﹣3）D. （2，﹣3）
【答案】B
【解析】
【详解】解：∵第二象限内点的横坐标是负数，纵坐标是正数，
∴（2，3）、（-2，3）、（-2，-3）、（2，-3）中只有（-2，3）在第二象限．
故选：B．
4. 在实数，3.33，，，0.0444555…，，127，中，无理数个数有（ ）
A. 3个B. 4个C. 5个D. 6个
【答案】A
【解析】
【分析】本题考查了无理数的概念，无限不循环小数是无理数，初中范围内涉及到的无理数有三种：开方开不尽的数，如；特定意义的数，如；特定结构的数，如．根据无理数的概念逐一判断，即可得到答案．
【详解】解：，3.33，，127，，是有理数
无理数有，0.0444555…，，共3个，
故选：A
5. 如图所示，点在的延长线上，下列条件中能判断的是（ ）

A. B.
C. D.
【答案】A
【解析】
【分析】本题考查了平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
根据平行线判定定理即可直接作出判断．
【详解】解：．根据内错角相等，两直线平行即可证得；
B．根据内错角相等，两直线平行即可证得，不能证；
C．根据内错角相等，两直线平行即可证得，不能证；
D．根据同旁内角互补，两直线平行，即可证得，不能证．
故选：A．
6. 点P位于x轴下方，y轴右侧，距离x轴4个单位长度，距离y轴2个单位长度，那么点P的坐标是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了象限内点的坐标特征，点到坐标轴的距离，掌握第一象限；第二象限；第三象限；第四象限是解题关键．先判断点P位于第四象限，再根据与坐标轴的距离，即可得到点的坐标．
【详解】解：点P位于x轴下方，y轴右侧，距离x轴4个单位长度，
点P位于第四象限，
距离x轴4个单位长度，距离y轴2个单位长度，
点P的坐标是，
故选：B．
7. 如图所示，将含有角的三角板的直角顶点放在相互平行的两条直线其中一条上，若，则的度数（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了平行线的判定和性质，三角板的角度计算，正确作平行线是解题关键．过点作，由平行线的性质可知，，，由三角板可知，，即可求出的度数．
详解】解：如图，标记各点，过点作，
，
，
，
，
由三角板可知，，
，
，
故选：D
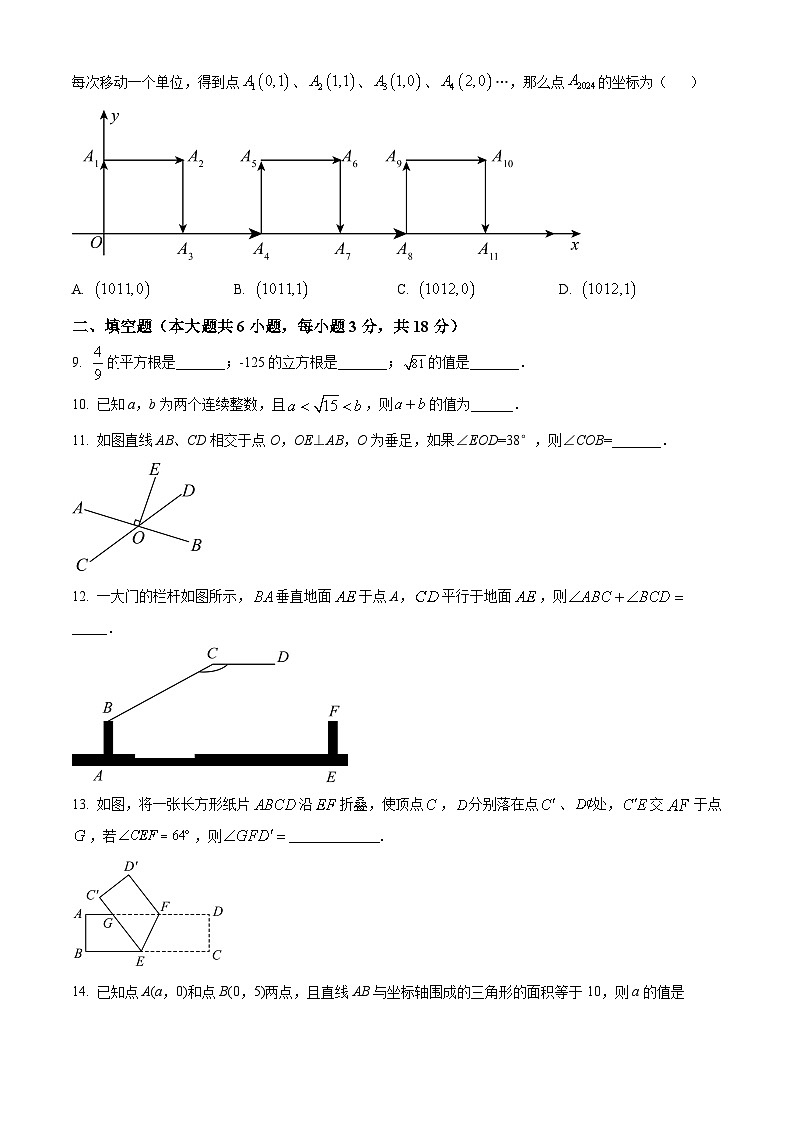
8. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每次移动一个单位，得到点、、、…，那么点的坐标为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了坐标的规律问题，观察直角坐标系，得出（为自然数），从而得到，即可得到点的坐标．
【详解】解：由直角坐标系可知，，，，……
（为自然数），
，
，
，
故选：C．
二、填空题（本大题共6小题，每小题3分，共18分）
9. 的平方根是_______；-125的立方根是_______；的值是_______．
【答案】 ①. ②. -5 ③. 9
【解析】
【分析】根据平方根、立方根、算术平方根的定义，即可解答．
【详解】的平方根是，-125的立方根是-5，的值是9，
故答案为：；-5；9．
【点睛】本题考查了平方根、立方根、算术平方根，熟练掌握它们的定义及运算方法是解答的关键．
10. 已知a，b为两个连续整数，且，则的值为______．
【答案】7
【解析】
【分析】本题主要考查无理数的估算，熟练掌握无理数的估算是解题的关键．根据，可得：a，b的值，进而即可求解．
【详解】解：∵，
又∵、为两个连续整数，，
∴，，
，
故答案为：7．
11. 如图直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38°，则∠COB=_______．

【答案】128°##128度
【解析】
【分析】根据垂直的定义得出∠AOE＝90°，最后根据∠COB＝∠AOD＝∠AOE +∠EOD进行求解．
【详解】∵OE⊥AB，∠EOD=38°，
∴∠AOE＝90°，
∴∠COB＝∠AOD＝∠AOE +∠EOD＝90°+38°＝128°，
故答案为：128°．
【点睛】本题考查垂直的定义，对顶角的性质，熟练掌握对顶角相等是解题的关键．
12. 一大门的栏杆如图所示，垂直地面于点A，平行于地面，则_____．
【答案】
【解析】
【分析】本题主要考查了平行线的性质，两直线平行，同旁内角互补．正确作出辅助线是解题的关键．过B作，则．根据平行线的性质即可求解．
【详解】解：过B作，
∵，
∴，
∴，
又∵，
∴，
∴，
∴．
故答案为：．
13. 如图，将一张长方形纸片沿折叠，使顶点，分别落在点、处，交于点，若，则_____________.
【答案】##52度
【解析】
【分析】根据题意可得，然后利用平行线的性质可得，从而利用平角定义求出，再利用折叠的性质可得，最后利用角的和差关系进行计算即可解答．
【详解】解：，
，
，
由折叠得：，
，
故答案为．
【点睛】本题考查了平行线的性质及折叠的性质，熟练掌握平行线的性质是解题的关键．
14. 已知点A(a，0)和点B(0，5)两点，且直线AB与坐标轴围成的三角形的面积等于10，则a的值是______ ．
【答案】±4
【解析】
【详解】解：∵点A(a，0)和点B(0，5)，
∴△OAB的两边长分别为|a|与5，
∴S△OAB=，
解得：a=4或a=-4，
即a的值为±4．
故答案为：±4．
三、（本大题共4小题，每小题6分，共24分）
15. 计算：
（1）
（2）|﹣2|﹣
【答案】（1）8；（2）
【解析】
【分析】（1）直接利用算术平方根以及立方根的性质分别化简得出答案；
（2）直接利用绝对值以及二次根式的性质化简得出答案．
【详解】解：（1）原式=；
（2）原式=．
【点睛】此题主要考查了实数运算，正确化简各数是解题关键．
16. 如图，直线，点在直线上，且，，求的度数．

【答案】
【解析】
【分析】先利用，求出，再利用平行线的性质求出即可．
详解】解： 标记如下图所示：

∵，，
∴
又∵，
∴，
∵，
∴．
【点睛】本题考查平行线的性质，垂直的定义，掌握平行线的性质是解题的关键．
17. 已知的立方根是3，的算术平方根是4，c是的整数部分．
（1）求a，b，c值；
（2）求的平方根．
【答案】（1），，
（2）
【解析】
【分析】（1）根据立方根和算术平方根的定义即可求出a、b，估算出的范围即可求出c；
（2）将a、b、c的值代入所求式子计算，再根据平方根的定义解答．
【小问1详解】
∵的立方根是3，的算术平方根是4，
∴，，
∴，，
∵，
∴，
∵c是的整数部分，
∴．
【小问2详解】
将，，代入得：，
∴的平方根是．
【点睛】本题考查了算术平方根、平方根和立方根的定义，属于基础题型，熟练掌握这三者的概念是关键．
18. 完成下面的证明：
如图，点E在直线上，点B在直线上，若，．
求证：．

证明：∵，
又∵______（对顶角相等）
∴，
∴（____________）
∴（______）
又∵，
∴，
∴（______）
∴（______）
【答案】；同位角相等，两直线平行；C；两直线平行，同位角相等；内错角相等，两直线平行；两直线平行，内错角相等
【解析】
【分析】本题考查了平行线的判定和性质，分别证明，，即可得到结论．
【详解】证明：∵，
又∵（对顶角相等）
∴，
∴（同位角相等，两直线平行）
∴（两直线平行，同位角相等）
又∵，
∴，
∴（内错角相等，两直线平行）
∴（两直线平行，内错角相等）．
四、（本大题共3小题，每小题8分，共24分）
19. 如图，的顶点．若向右平移4个单位长度，再向下平移3个单位长度得到，且点C的对应点坐标是．
（1）画出，并直接写出点的坐标；
（2）若内有一点经过以上平移后的对应点为，直接写出点的坐标；
（3）求的面积．
【答案】（1）见解析过程，点
（2）点
（3）
【解析】
【分析】本题考查坐标与平移，熟练掌握平移的性质是解题的关键．．
（1）根据平移规则，画出，进而写出点的坐标即可；
（2）根据平移规则，写出的坐标即可；
（3）分割法求三角形的面积即可．
【小问1详解】
如图所示：
∴点；
【小问2详解】
∵向右平移4个单位长度，再向下平移3个单位长度得到，
∴点；
【小问3详解】
．
20. 如图，长方形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（6，0）,（0，10），点B在第一象限内.
（1）写出点B的坐标，并求长方形OABC的周长；
（2）若有过点C的直线CD把长方形OABC的周长分成3:5两部分，D为直线CD与长方形的边的交点，求点D的坐标.
【答案】（1）点B的坐标为（6，10），长方形OABC的周长为32；（2）点D的坐标为（2，0）或（6，4）
【解析】
【详解】：解：（1）∵A（6，0），C（0，10），
∴OA=6，OC=10．
∵四边形OABC是长方形，
∴BC=OA=6，AB=OC=10，
∴点B的坐标为（6，10）．
∵OC=10，OA=6，
∴长方形OABC的周长为：2×（6+10）=32．
（2）∵CD把长方形OABC的周长分为3：5两部分，
∴被分成的两部分的长分别为12和20．
①当点D在AB上时，如图，AD=20-10-6=4，所以点D的坐标为（6，4）．
②当点D在OA上时，如图，OD=12-10=2，所以点D的坐标为（2，0）．
21. 如图，∠ADE+∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E．
(1)AD与BC平行吗？请说明理由；
(2)AB与EF的位置关系如何？为什么？
(3)若AF平分∠BAD，试说明：∠E+∠F＝90°
【答案】（1）AD∥BC，见解析；（2）AB∥EF，见解析；（3）见解析.
【解析】
【分析】（1）欲证明AD∥BC，只要证明∠ADF=∠BCF即可；
（2）结论：AB∥EF，只要证明∠E=∠ABE 即可；
（3）只要证明∠OAB+∠OBA=90°即可解决问题；
【详解】解：（1）结论：AD∥BC．
理由如下：
∵∠ADE+∠ADF=180°，
∠ADE+∠BCF=180°，
∴∠ADF=∠BCF，
∴AD∥BC；
（2）结论：AB与EF的位置关系是：AB∥EF．
理由：
∵BE平分∠ABC，
∴∠ABE= ∠ABC．
又∵∠ABC=2∠E，
即∠E=∠ABC，
∴∠E=∠ABE．
∴AB∥EF；
（3）∵AD∥BC，
∴∠DAB+∠CBA=180°，
∵∠OAB=DAB，∠OBA=∠CBA，
∴∠OAB+∠OBA=90°，
∴∠EOF=∠AOB=90°，
∴∠E+∠F=90°．
【点睛】本题考查平行线的判定和性质、角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
五、（本大题共1小题，每小题10分，共10分）
22. 如图1，，在、内有一条折线．
（1）求证：．
（2）如图2，已知的平分线与的平分线相交于点Q，若，求的度数；
（3）如图3，已知，，直接写出与有什么关系．
【答案】（1）见解析 （2）
（3）
【解析】
【分析】（1）过点P作，可证，可得，，据此求出即可；
（2）由（1），可得，；然后根据的平分线与的平分线相交于点Q，推得，，进而可求出结果即可；
（3）仿照（2）的过程求解即可．
【小问1详解】
证明：如图1，过点P作，
∵，
∴，
∴，，
又∵，
∴．
【小问2详解】
解：如图2，
由（1），可得：，，
∵的平分线与的平分线相交于点Q，
∴，
∴
；
【小问3详解】
解：如图3，
由（1），可得：
，，
∵，，
∴
，
∴．
【点睛】此题考查了平行线的性质的应用，熟练掌握角平分线的定义和两直线平行，内错角相等是解答本题的关键．