专题18 特殊四边形及圆的相关证明与计算（17类重点考向）-备战2024年中考数学真题题源解密（全国通用）

这是一份专题18 特殊四边形及圆的相关证明与计算（17类重点考向）-备战2024年中考数学真题题源解密（全国通用），文件包含专题18特殊四边形及圆的相关证明与计算17类重点考向原卷版docx、专题18特殊四边形及圆的相关证明与计算17类重点考向解析版docx、专题18特殊四边形及圆的相关证明与计算17类重点考向考点回归docx等3份试卷配套教学资源，其中试卷共74页， 欢迎下载使用。

矩形
1．矩形的性质：
（1）四个角都是直角；
（2）对角线相等且互相平分；
（3）面积=长×宽=2S△ABD=4S△AOB．（如图）
2．矩形的判定：
（1）有一个角是直角的平行四边形是矩形；
（2）有三个角是直角的四边形是矩形；
（3）对角线相等的平行四边形是矩形．
直角三角形斜边上的中线
1.性质：在直角三角形中，斜边上的中线等于斜边的一半．（即直角三角形的外心位于斜边的中点）
2.定理：一个三角形，如果一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形．
该定理可以用来判定直角三角形．
菱形
1．菱形的性质：
（1）四边相等；
（2）对角线互相垂直、平分，一条对角线平分一组对角；
（3）面积=底×高=对角线乘积的一半．
2．菱形的判定：
（1）有一组邻边相等的平行四边形是菱形；
（2）对角线互相垂直的平行四边形是菱形；
（3）四条边都相等的四边形是菱形．
正方形
1．正方形的性质：
（1）四条边都相等，四个角都是直角；
（2）对角线相等且互相垂直平分；
（3）面积=边长×边长=2S△ABD=4S△AOB．
2．正方形的判定：
（1）有一个角是直角，且有一组邻边相等的平行四边形是正方形；
（2）一组邻边相等的矩形是正方形；
（3）一个角是直角的菱形是正方形；
（4）对角线相等且互相垂直、平分的四边形是正方形．
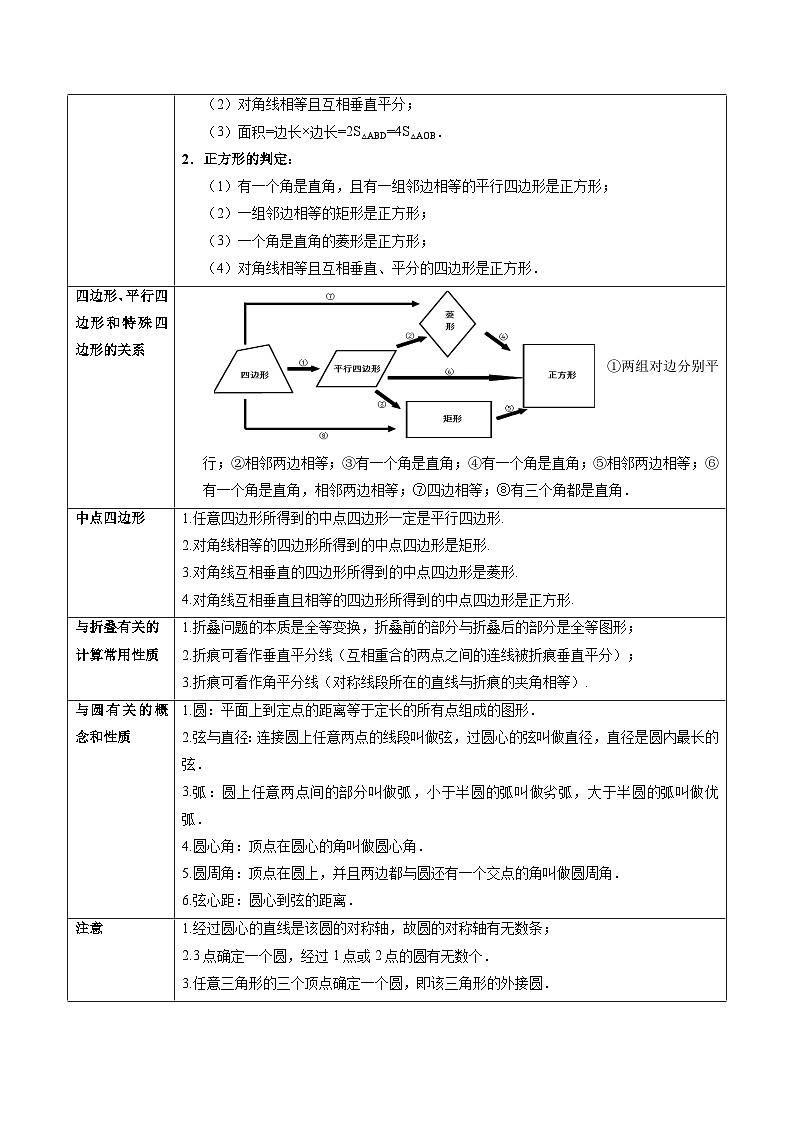
四边形、平行四边形和特殊四边形的关系
①两组对边分别平行；②相邻两边相等；③有一个角是直角；④有一个角是直角；⑤相邻两边相等；⑥有一个角是直角，相邻两边相等；⑦四边相等；⑧有三个角都是直角．
中点四边形
1.任意四边形所得到的中点四边形一定是平行四边形.
2.对角线相等的四边形所得到的中点四边形是矩形.
3.对角线互相垂直的四边形所得到的中点四边形是菱形.
4.对角线互相垂直且相等的四边形所得到的中点四边形是正方形.
与折叠有关的计算常用性质
1.折叠问题的本质是全等变换，折叠前的部分与折叠后的部分是全等图形；
2.折痕可看作垂直平分线（互相重合的两点之间的连线被折痕垂直平分）；
3.折痕可看作角平分线（对称线段所在的直线与折痕的夹角相等）.
与圆有关的概念和性质
1.圆：平面上到定点的距离等于定长的所有点组成的图形．
2.弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．
3.弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．
4.圆心角：顶点在圆心的角叫做圆心角．
5.圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．
6.弦心距：圆心到弦的距离．
注意
1.经过圆心的直线是该圆的对称轴，故圆的对称轴有无数条；
2.3点确定一个圆，经过1点或2点的圆有无数个．
3.任意三角形的三个顶点确定一个圆，即该三角形的外接圆．
垂径定理及其推论
1．垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．
2．推论
①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；
②弦的垂直平分线经过圆心，并且平分弦所对的两条弧．
圆心角、弧、弦的关系
1．定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．
2．推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
圆周角定理及其推论
1．定理：一条弧所对的圆周角等于它所对的圆心角的一半．
2．推论：
①在同圆或等圆中，同弧或等弧所对的圆周角相等．
②直径所对的圆周角是直角．
③圆内接四边形的对角互补．
点与圆的位置关系
设点到圆心的距离为d．
（1）dr⇔点在⊙O外．
判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．
直线和圆的位置关系
位置关系
相离
相切
相交
图形
公共点个数
0个
1个
2个
数量关系
d>r
d=r
d