2025版高考数学一轮总复习知识梳理训练题第8章平面解析几何第1讲直线的倾斜角斜率与直线的方程

这是一份2025版高考数学一轮总复习知识梳理训练题第8章平面解析几何第1讲直线的倾斜角斜率与直线的方程，共3页。试卷主要包含了定义，直线的方向向量与斜率的关系等内容，欢迎下载使用。

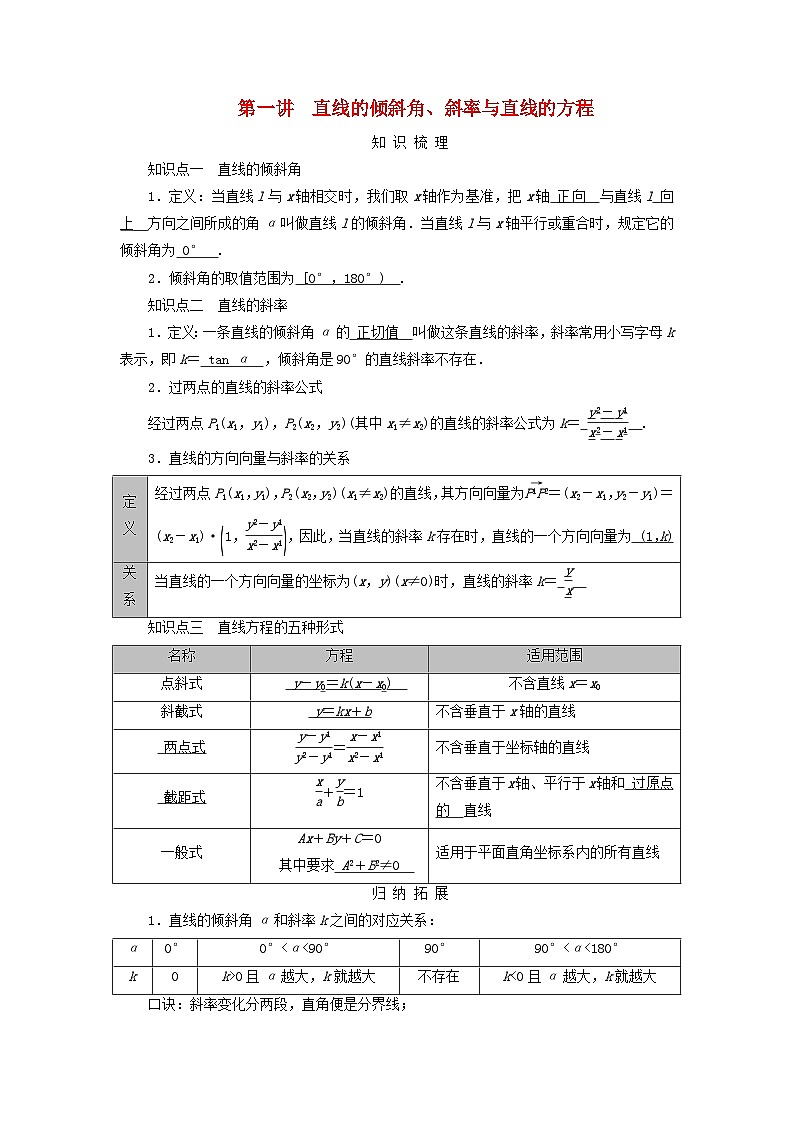
知识点一 直线的倾斜角
1．定义：当直线l与x轴相交时，我们取x轴作为基准，把x轴 正向 与直线l 向上 方向之间所成的角α叫做直线l的倾斜角．当直线l与x轴平行或重合时，规定它的倾斜角为 0° .
2．倾斜角的取值范围为 [0°，180°) .
知识点二 直线的斜率
1．定义：一条直线的倾斜角α的 正切值 叫做这条直线的斜率，斜率常用小写字母k表示，即k＝ tan α ，倾斜角是90°的直线斜率不存在．
2．过两点的直线的斜率公式
经过两点P1(x1，y1)，P2(x2，y2)(其中x1≠x2)的直线的斜率公式为k＝ eq \f(y2－y1,x2－x1) .
3．直线的方向向量与斜率的关系
知识点三 直线方程的五种形式
归 纳 拓 展
1．直线的倾斜角α和斜率k之间的对应关系：
口诀：斜率变化分两段，直角便是分界线；
小正大负皆递增，分类讨论记心中．
2．特殊直线的方程
(1)过点P1(x1，y1)垂直于x轴的直线方程为x＝x1；
(2)过点P1(x1，y1)垂直于y轴的直线方程为y＝y1；
(3)过原点的直线的方程为x＝my.
3．谨记以下几点
(1)“截距”是直线与坐标轴交点的坐标值，它可正，可负，也可以是零，而“距离”是一个非负数．求与截距有关的直线方程时应注意过原点的特殊情况是否满足题意．
(2)当直线与x轴不垂直时，可设直线的方程为y＝kx＋b；当不确定直线的斜率是否存在时，可设直线的方程为x＝my＋b.
(3)A，B，C三点共线⇔kAB＝kAC(或kAB＝kBC，或kAC＝kBC)．
(4)直线Ax＋By＋C＝0(A2＋B2≠0)的一个方向向量a＝(－B，A)．
双 基 自 测
题组一 走出误区
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)坐标平面内的任何一条直线均有倾斜角与斜率．( × )
(2)直线的倾斜角越大，其斜率就越大．( × )
(3)斜率相等的两直线的倾斜角一定相等．( √ )
(4)经过定点A(0，b)的直线都可以用方程y＝kx＋b表示．( × )
(5)不经过原点的直线都可以用eq \f(x,a)＋eq \f(y,b)＝1表示．( × )
(6)经过任意两个不同的点P1(x1，y1)，P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示．( √ )
题组二 走进教材
2．(选择性必修1P58T7)经过两点A(4,2y＋1)，B(2，－3)的直线的倾斜角为eq \f(3π,4)，则y＝( B )
A．－1 B．－3
C．0 D．2
[解析] 由eq \f(2y＋1－－3,4－2)＝eq \f(2y＋4,2)＝y＋2，
得y＋2＝taneq \f(3π,4)＝－1，∴y＝－3.
3．(选择性必修1P67T7)过点P(2,3)且在两坐标轴上截距相等的直线方程为 3x－2y＝0或x＋y－5＝0 .
[解析] 当截距为0时，直线方程为3x－2y＝0；
当截距不为0时，设直线方程为eq \f(x,a)＋eq \f(y,a)＝1，
则eq \f(2,a)＋eq \f(3,a)＝1，解得a＝5.所以直线方程为x＋y－5＝0.
题组三 走向高考
4．(2022·北京高考真题)若直线2x＋y－1＝0是圆(x－a)2＋y2＝1的一条对称轴，则a＝( A )
A.eq \f(1,2) B．－eq \f(1,2)
C．1 D．－1
[解析] 由题意知圆心坐标为(a,0)，又直线2x＋y－1＝0是圆(x－a)2＋y2＝1的一条对称轴，所以圆心在直线上，即2a＋0－1＝0，解得a＝eq \f(1,2).故选A.
5. (2021·山东高考真题)如右图，直线l的方程是( D )
A.eq \r(3)x－y－eq \r(3)＝0
B.eq \r(3)x－2y－eq \r(3)＝0
C.eq \r(3)x－3y－1＝0
D．x－eq \r(3)y－1＝0
[解析] 由图可得直线的倾斜角为30°，所以斜率k＝tan 30°＝eq \f(\r(3),3)，又直线l与x轴的交点为(1,0)，所以直线的点斜式方程可得l：y－0＝eq \f(\r(3),3)(x－1)，即x－eq \r(3)y－1＝0.故选D.定
义
经过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线，其方向向量为eq \(P1P2,\s\up6(→))＝(x2－x1，y2－y1)＝(x2－x1)·eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(y2－y1,x2－x1)))，因此，当直线的斜率k存在时，直线的一个方向向量为 (1，k)
关
系
当直线的一个方向向量的坐标为(x，y)(x≠0)时，直线的斜率k＝ eq \f(y,x)
名称
方程
适用范围
点斜式
y－y0＝k(x－x0)
不含直线x＝x0
斜截式
y＝kx＋b
不含垂直于x轴的直线
两点式
eq \f(y－y1,y2－y1)＝eq \f(x－x1,x2－x1)
不含垂直于坐标轴的直线
截距式
eq \f(x,a)＋eq \f(y,b)＝1
不含垂直于x轴、平行于x轴和 过原点的 直线
一般式
Ax＋By＋C＝0
其中要求 A2＋B2≠0
适用于平面直角坐标系内的所有直线
α
0°
0°<α<90°
90°
90°<α<180°
k
0
k>0且α越大，k就越大
不存在
k<0且α越大，k就越大