2025版高考数学一轮总复习知识梳理训练题第7章立体几何第5讲空间向量及其运算

这是一份2025版高考数学一轮总复习知识梳理训练题第7章立体几何第5讲空间向量及其运算，共7页。试卷主要包含了空间向量的有关概念，空间向量中的有关定理，空间向量的数量积及运算律，向量法证明空间的线面平行或垂直等内容，欢迎下载使用。
知识点一 空间向量的有关概念
1．空间向量的有关概念
(1)空间向量：在空间中，具有 大小 和 方向 的量叫做空间向量，其大小叫做向量的 长度 或 模 .
(2)零向量：长度为 0 的向量，记作0；
零向量与任意向量共线，0∥a；
单位向量：模为 1 的向量；
相反向量：与向量a长度相等而方向相反的向量，叫做a的相反向量，记作－a；
相等向量：方向 相同 且模 相等 的向量．
(3)共线向量：如果表示空间向量的有向线段所在的直线 平行 或 重合 ，则这些向量叫做 共线向量 或 平行向量 .
(4)共面向量：平行于同一 平面 的向量叫做共面向量．
2．空间向量中的有关定理
(1)共线向量定理：对空间任意两个向量a，b(b≠0)，a∥b⇔存在唯一确定的λ∈R，使a＝λb.
(2)共面向量定理：若两个向量a，b不共线，则向量p与向量a，b共面⇔存在唯一的有序实数对(x，y)，使p＝xa＋yb.
(3)空间向量基本定理：如果三个向量a，b，c不共面，那么对空间任一向量p，存在唯一的有序实数组{x，y，z}使得p＝xa＋yb＋zc.其中{a，b，c}叫做空间的一个基底．
3．空间向量的数量积及运算律
(1)已知两个非零向量a，b，在空间任取一点O，作eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，则∠AOB叫做向量a，b的夹角，记作 〈a，b〉 ，其范围是 0≤〈a，b〉≤π ，若〈a，b〉＝eq \f(π,2)，则称a与b 互相垂直 ，记作a⊥b.
向量a，b的数量积a·b＝ |a||b|cs〈a，b〉 .
(2)空间向量数量积的运算律
结合律：(λa)·b＝λ(a·b)；
交换律：a·b＝b·a；
分配律：a·(b＋c)＝ a·b＋a·c .
知识点二 空间向量的坐标表示及其应用
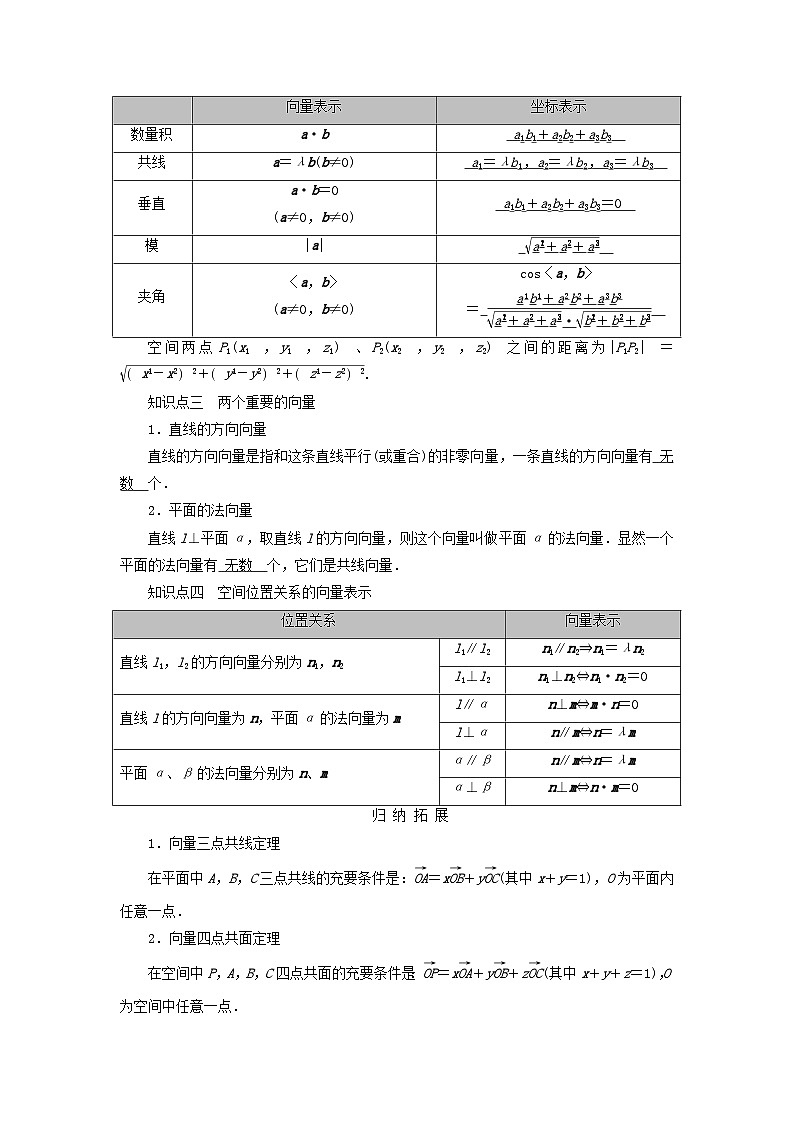
设a＝(a1，a2，a3)，b＝(b1，b2，b3)．则
空间两点P1(x1，y1，z1)、P2(x2，y2，z2)之间的距离为|P1P2|＝eq \r(x1－x22＋y1－y22＋z1－z22).
知识点三 两个重要的向量
1．直线的方向向量
直线的方向向量是指和这条直线平行(或重合)的非零向量，一条直线的方向向量有 无数 个．
2．平面的法向量
直线l⊥平面α，取直线l的方向向量，则这个向量叫做平面α的法向量．显然一个平面的法向量有 无数 个，它们是共线向量．
知识点四 空间位置关系的向量表示
归 纳 拓 展
1．向量三点共线定理
在平面中A，B，C三点共线的充要条件是：eq \(OA,\s\up6(→))＝xeq \(OB,\s\up6(→))＋yeq \(OC,\s\up6(→))(其中x＋y＝1)，O为平面内任意一点．
2．向量四点共面定理
在空间中P，A，B，C四点共面的充要条件是：eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))＋zeq \(OC,\s\up6(→))(其中x＋y＋z＝1)，O为空间中任意一点．
3．|a|2＝a·a；|a·b|≤|a|·|b|.
4．a·b>0⇔a、b的夹角为锐角或0角．即“a·b>0”是“a、b的夹角为锐角”的必要不充分条件．
5．向量法证明空间的线面平行或垂直
①a，b为平面α的基向量，若eq \(AB,\s\up6(→))＝λa＋μb(λ，μ∈R)，AB⊄α，则AB∥α.
②若n为平面α的法向量，eq \(AB,\s\up6(→))·n＝0.AB⊄α，则AB∥α.
③a，b为平面α的基向量，若eq \b\lc\{\rc\ (\a\vs4\al\c1(\(AB,\s\up6(→))·a＝0，,\(AB,\s\up6(→))·b＝0，))则AB⊥α.
双 基 自 测
题组一 走出误区
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)空间中任意两个非零向量a，b共面．( √ )
(2)在向量的数量积运算中(a·b)·c＝a·(b·c)．( × )
(3)对于非零向量b，由a·b＝b·c，则a＝c.( × )
(4)两向量夹角的范围与两异面直线所成角的范围相同．( × )
(5)平面的单位法向量是唯一确定的．( × )
(6)若两平面的法向量垂直，则两平面垂直．( √ )
题组二 走进教材
2．(选择性必修1P10T5)如图，在三棱柱ABC－A1B1C1中，M为A1C1的中点，若eq \(BA,\s\up6(→))＝a，eq \(BC,\s\up6(→))＝b，eq \(BB1,\s\up6(→))＝c，则下列向量与eq \(BM,\s\up6(→))相等的是( D )
A．－eq \f(1,2)a－eq \f(1,2)b＋c B．eq \f(1,2)a＋eq \f(1,2)b－c
C．－eq \f(1,2)a＋eq \f(1,2)b＋c D．eq \f(1,2)a＋eq \f(1,2)b＋c
[解析] ∵在三棱柱ABC－A1B1C1中，M为A1C1的中点，
∴eq \(BM,\s\up6(→))＝eq \(BA,\s\up6(→))＋eq \(AA1,\s\up6(→))＋eq \(A1M,\s\up6(→))
＝a＋c＋eq \f(1,2)eq \(AC,\s\up6(→))
＝a＋c＋eq \f(1,2)(eq \(BC,\s\up6(→))－eq \(BA,\s\up6(→)))
＝a＋c＋eq \f(1,2)(b－a)
＝eq \f(1,2)a＋eq \f(1,2)b＋c.故选D.
3．(选择性必修1P14T2)(2023·河南驻马店模拟)在三棱柱ABC－A1B1C1中，底面边长和侧棱长都相等，∠BAA1＝∠CAA1＝60°，则异面直线AB1与BC1所成角的余弦值为( A )
A.eq \f(\r(6),6) B．eq \f(\r(3),3)
C．eq \f(1,6) D．eq \f(1,3)
[解析] 解法一：记eq \(AB,\s\up6(→))＝a，eq \(AC,\s\up6(→))＝b，eq \(AA1,\s\up6(→))＝c，
由题意知a、b、c两两夹角均为eq \f(π,3)，设AB＝1，则eq \(AB1,\s\up6(→))＝a＋c，eq \(BC1,\s\up6(→))＝－a＋b＋c，
∴|eq \(AB1,\s\up6(→))|＝eq \r(a＋c2)＝eq \r(3)，
|eq \(BC1,\s\up6(→))|＝eq \r(－a＋b＋c2)＝eq \r(2)，
∴cs〈eq \(AB1,\s\up6(→))，eq \(BC1,\s\up6(→))〉＝eq \f(\(AB1,\s\up6(→))·\(BC1,\s\up6(→)),|\(AB1,\s\up6(→))||\(BC1,\s\up6(→))|)＝eq \f(\r(6),6).
解法二：将三棱柱补成平行六面体(如图)，连AD1，B1D1，则AD1∥BC1，
∴∠B1AD1或其补角即为AB1与BC1所成的角，设AB＝1，则AB1＝eq \r(3)，
AD1＝BC1＝eq \r(2)，B1D1＝eq \r(3)，
∴cs∠B1AD1＝eq \f(\f(AD1,2),AB1)＝eq \f(\r(2),2\r(3))＝eq \f(\r(6),6).
题组三 走向高考
4．(多选题)(2021·全国新高考Ⅱ)如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点，则满足MN⊥OP的是( BC )
[解析] 不妨设正方体棱长为2，
对于A，
eq \(MN,\s\up6(→))＝(－2,2,0)，eq \(OP,\s\up6(→))＝(－1,1,1)，
∴eq \(MN,\s\up6(→))·eq \(OP,\s\up6(→))＝4≠0，
∴MN不垂直OP.
对于B，
eq \(MN,\s\up6(→))＝(－2,0,2)，eq \(OP,\s\up6(→))＝(1，－1,1)，
∴eq \(MN,\s\up6(→))·eq \(OP,\s\up6(→))＝0，∴MN⊥OP.
对于C，
eq \(MN,\s\up6(→))＝(－2,0，－2)，eq \(OP,\s\up6(→))＝(－1，－1,1)，
∴eq \(MN,\s\up6(→))·eq \(OP,\s\up6(→))＝0，
∴MN⊥OP.
对于D，
eq \(MN,\s\up6(→))＝(0，－2,2)，eq \(OP,\s\up6(→))＝(1,0,2)，
∴eq \(MN,\s\up6(→))·eq \(OP,\s\up6(→))＝4≠0，
∴MN不垂直OP.故选BC.
5．(多选题)(2021·全国新课标Ⅰ卷)在正三棱柱ABC－A1B1C1中，AB＝AA1＝1，点P满足eq \(BP,\s\up6(→))＝λeq \(BC,\s\up6(→))＋μeq \(BB1,\s\up6(→))，其中λ∈[0,1]，μ∈[0,1]，则( BD )
A．当λ＝1时，△AB1P的周长为定值
B．当μ＝1时，三棱锥P－A1BC的体积为定值
C．当λ＝eq \f(1,2)时，有且仅有一个点P，使得A1P⊥BP
D．当μ＝eq \f(1,2)时，有且仅有一个点P，使得A1B⊥平面AB1P
[解析] 易知，点P在矩形BCC1B1内部(含边界)．对于A，当λ＝1时，eq \(BP,\s\up6(→))＝eq \(BC,\s\up6(→))＋μeq \(BB1,\s\up6(→))＝eq \(BC,\s\up6(→))＋μeq \(CC1,\s\up6(→))，即此时P∈线段CC1，△AB1P周长不是定值，故A错误；对于B，当μ＝1时，eq \(BP,\s\up6(→))＝λeq \(BC,\s\up6(→))＋eq \(BB1,\s\up6(→))＝eq \(BB1,\s\up6(→))＋λeq \(B1C1,\s\up6(→))，故此时P点轨迹为线段B1C1，而B1C1∥BC，B1C1∥平面A1BC，则有P到平面A1BC的距离为定值，所以其体积为定值，故B正确；对于C，当λ＝eq \f(1,2)时，eq \(BP,\s\up6(→))＝eq \f(1,2)eq \(BC,\s\up6(→))＋μeq \(BB1,\s\up6(→))，取BC，B1C1中点分别为Q，H，则eq \(BP,\s\up6(→))＝eq \(BQ,\s\up6(→))＋μeq \(QH,\s\up6(→))，所以P点轨迹为线段QH，不妨建系解决，建立空间直角坐标系如图，A1eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)，0，1))，P(0,0，μ)，Beq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,2)，0))，则eq \(A1P,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，0，μ－1))，eq \(BP,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(1,2)，μ))，eq \(A1P,\s\up6(→))·eq \(BP,\s\up6(→))＝μ(μ－1)＝0，所以μ＝0或μ＝1.故H，Q均满足，故C错误；对于D，当μ＝eq \f(1,2)时，eq \(BP,\s\up6(→))＝λeq \(BC,\s\up6(→))＋eq \f(1,2)eq \(BB1,\s\up6(→))，取BB1，CC1中点为M，N.eq \(BP,\s\up6(→))＝eq \(BM,\s\up6(→))＋λeq \(MN,\s\up6(→))，所以P点轨迹为线段MN.设Peq \b\lc\(\rc\)(\a\vs4\al\c1(0，y0，\f(1,2)))，因为Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)，0，0))，所以eq \(AP,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，y0，\f(1,2)))，eq \(A1B,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，\f(1,2)，－1))，所以eq \f(3,4)＋eq \f(1,2)y0－eq \f(1,2)＝0⇒y0＝－eq \f(1,2)，此时P与N重合，故D正确．故选BD.
向量表示
坐标表示
数量积
a·b
a1b1＋a2b2＋a3b3
共线
a＝λb(b≠0)
a1＝λb1，a2＝λb2，a3＝λb3
垂直
a·b＝0
(a≠0，b≠0)
a1b1＋a2b2＋a3b3＝0
模
|a|
eq \r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))
夹角
〈a，b〉
(a≠0，b≠0)
cs〈a，b〉
＝ eq \f(a1b1＋a2b2＋a3b3,\r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))·\r(b\\al(2,1)＋b\\al(2,2)＋b\\al(2,3)))
位置关系
向量表示
直线l1，l2的方向向量分别为n1，n2
l1∥l2
n1∥n2⇒n1＝λn2
l1⊥l2
n1⊥n2⇔n1·n2＝0
直线l的方向向量为n，平面α的法向量为m
l∥α
n⊥m⇔m·n＝0
l⊥α
n∥m⇔n＝λm
平面α、β的法向量分别为n、m
α∥β
n∥m⇔n＝λm
α⊥β
n⊥m⇔n·m＝0