浙江省杭州市萧山区南片2023-2024学年八年级下学期期中数学试卷+

这是一份浙江省杭州市萧山区南片2023-2024学年八年级下学期期中数学试卷+，共16页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。

1．当a＝6时，二次根式的值为（ ）
A．1B．2C．3D．4
2．下列方程中，是一元二次方程的是（ ）
A．x2﹣2x＝0B．xy＝1C．2x2﹣y2＝0D．
3．小康同学连续15天进行了体温测量，结果统计如如表：
这15天中，小康体温的众数为（ ）
A．36.3℃B．36.4℃C．36.6℃D．36.7℃
4．对于反比例函数，下列说法不正确的是（ ）
A．点（﹣3，1）在它的图象上
B．它的图象在第二、四象限
C．当x＞0时，y随x的增大而增大
D．当x＜0时，y随x的增大而减小
5．已知一元二次方程3x2﹣mx﹣m＝0的一个根是2，则m的值为（ ）
A．2B．3C．4D．6
6．在直角坐标系中，有四个点P（2，），Q（﹣，），M（﹣2，），N（，2），则这四个点中到原点距离最远的点是（ ）
A．PB．QC．MD．N
7．水果店里有一批大小不一的西瓜，餐厅经理选择了部分大小均匀的西瓜．设水果店里的西瓜的质量（单位：kg）平均数和方差分别为，s2，餐厅经理选购的西瓜的质量的平均数和方差分别为，，则下列结论一定成立的是（ ）
A．B．C．D．
8．设，则对于实数m的范围判断正确的是（ ）
A．4＜m＜5B．5＜m＜6C．6＜m＜7D．7＜m＜8
9．已知关于x的一元二次方程kx2﹣（4k﹣1）x+4k﹣3＝0有两个不相等的实数根，则实数k的取值范围是（ ）
A．k＜B．k＜且k≠0
C．k＞﹣D．k＞﹣且k≠0
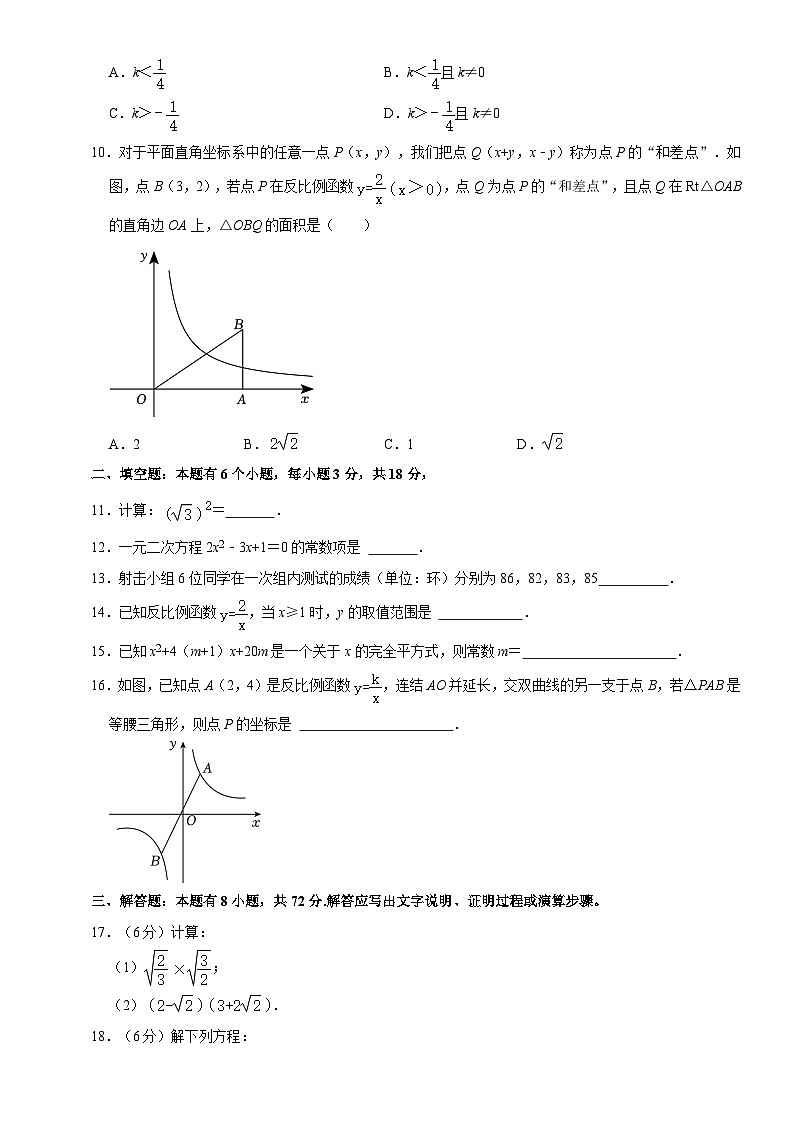
10．对于平面直角坐标系中的任意一点P（x，y），我们把点Q（x+y，x﹣y）称为点P的“和差点”．如图，点B（3，2），若点P在反比例函数，点Q为点P的“和差点”，且点Q在Rt△OAB的直角边OA上，△OBQ的面积是（ ）
A．2B．C．1D．
二、填空题：本题有6个小题，每小题3分，共18分，
11．计算：＝ ．
12．一元二次方程2x2﹣3x+1＝0的常数项是 ．
13．射击小组6位同学在一次组内测试的成绩（单位：环）分别为86，82，83，85 ．
14．已知反比例函数，当x≥1时，y的取值范围是 ．
15．已知x2+4（m+1）x+20m是一个关于x的完全平方式，则常数m＝ ．
16．如图，已知点A（2，4）是反比例函数，连结AO并延长，交双曲线的另一支于点B，若△PAB是等腰三角形，则点P的坐标是 ．
三、解答题：本题有8小题，共72分.解答应写出文字说明、证明过程或演算步骤。
17．（6分）计算：
（1）；
（2）．
18．（6分）解下列方程：
（1）x2﹣5x＝0；
（2）x2﹣10x+16＝0．
19．（8分）已知，，求代数式a2+b2﹣4a+4的值．
20．（8分）某校对九年级3个班级进行综合素质考评，下表是它们五项素质考评得分表（以分为单位，每项满分为10分）．
（1）计算各班五项考评分的平均数．
（2）现要从三个班级中选送一个班级为市级先进班集体候选班，并设定如下规则：行为规范：学习成绩：校运动会：艺术获奖：劳动卫生＝3：3：2：1：1．请通过计算说明推荐市级先进班集体候选班是哪个班？
21．（10分）把一根长为80cm的绳子剪成两段，并把每一段绳子围成一个正方形．
（1）要使这两个正方形的面积之和等于200cm2，该怎么剪？
（2）这两个正方形面积之和可能等于488cm2吗？
22．（10分）如图，已知A（﹣4，n），B（2，﹣4）是反比例函数y＝
（1）求反比例函数和一次函数的解析式；
（2）求△AOB的面积；
（3）根据图象直接写出不等式ax+b﹣＜0的解集．
23．（12分）【综合与实践】
[问题情境]对于关于x的一元二次方程ax2+bx+c＝0（a，b，c为常数，且a≠0），求方程的根的实质是找到一个x的具体的值，代入之后等式成立．一般情况下，这就说明这个方程有两个根，且两根与a，b
[操作判断]项目研究小组经过讨论得到两个结论：
（1）当a+b+c＝0时，则一元二次方程ax2+bx+c＝0必有一根是1．
（2）当a+c＝b时，则一元二次方程ax2+bx+c＝0必有一根是﹣1．
请判断两个结论的真假，并说明原因．
[实践探究]项目研究小组经过讨论编制了以下问题，请帮助解决：
方程（2023x）2﹣2022×2024x﹣1＝0的较大的根为p，方程x2+2023x﹣2024＝0的较小的根为q，求p﹣q的值．
24．（12分）如图，直线y＝﹣x﹣2分别交x轴、y轴于A、B两点（m≠0）在第二象限内的交点为C，CD⊥y轴于点D
（1）求双曲线的解析式；
（2）设点Q是双曲线上的一点，且△QOB的面积是△AOB的面积的2倍，求点Q的坐标；
（3）在y轴上存在点P，使PA+PC最短，请直接写出点P的坐标．
浙江省杭州市萧山区南片2023-2024学年八年级下学期期中数学试卷
参考答案
一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项最符合题目要求。
1．当a＝6时，二次根式的值为（ ）
A．1B．2C．3D．4
【分析】将a＝6代入代数式求值即可．
【解答】解：当a＝6时，
＝
＝
＝6．
故选：B．
【点评】本题考查了二次根式的定义，将a＝6代入代数式求值是解题的关键．
2．下列方程中，是一元二次方程的是（ ）
A．x2﹣2x＝0B．xy＝1C．2x2﹣y2＝0D．
【分析】根据一元二次方程的定义逐项分析即可．
【解答】解：A．x2﹣2x＝8是一元二次方程，符合题意；
B．xy＝1是二元二次方程；
C.2x4﹣y2＝0是二元二次方程，不符合题意；
D．x7+4＝是分式方程；
故选：A．
【点评】本题考查了一元二次方程的定义，方程的两边都是整式，只含有一个未知数，并且整理后未知数的最高次数都是2，像这样的方程叫做一元二次方程．
3．小康同学连续15天进行了体温测量，结果统计如如表：
这15天中，小康体温的众数为（ ）
A．36.3℃B．36.4℃C．36.6℃D．36.7℃
【分析】根据众数的定义求解即可．
【解答】解：这15天中，小康体温的众数为36.6℃，
故选：C．
【点评】本题主要考查众数，一组数据中出现次数最多的数据叫做众数．
4．对于反比例函数，下列说法不正确的是（ ）
A．点（﹣3，1）在它的图象上
B．它的图象在第二、四象限
C．当x＞0时，y随x的增大而增大
D．当x＜0时，y随x的增大而减小
【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解．
【解答】解：A、∵﹣，∴点（﹣5，故本选项正确；
B、k＝﹣3＜0、四象限；
C、k＝﹣3＜0，y随x的增大而增大；
D、k＝﹣3＜4，y随x的增大而增大．
故选：D．
【点评】本题考查了反比例函数的性质，对于反比例函数（k≠0），（1）k＞0，反比例函数图象在一、三象限，在每一个象限内，y随x的增大而减小；（2）k＜0，反比例函数图象在第二、四象限内，在每一个象限内，y随x的增大而增大．
5．已知一元二次方程3x2﹣mx﹣m＝0的一个根是2，则m的值为（ ）
A．2B．3C．4D．6
【分析】把x＝2代入方程3x2﹣mx﹣m＝0得关于m的方程，解方程即可．
【解答】解：把x＝2代入方程3x5﹣mx﹣m＝0得：
12﹣2m﹣m＝2，
12﹣3m＝0，
6m＝12，
m＝4，
故选：C．
【点评】本题主要考查了一元二次方程的解，解题关键是熟练掌握一元二次方程的解是使方程左右两边相等的未知数的值．
6．在直角坐标系中，有四个点P（2，），Q（﹣，），M（﹣2，），N（，2），则这四个点中到原点距离最远的点是（ ）
A．PB．QC．MD．N
【分析】由P（2，），得PO2＝＝7，同理得QO2＝8，MO2＝7，NO2＝7，故这四个点中到原点距离最远的点是Q．
【解答】解：由P（2，），
得PO3＝＝7，
同理得QO2＝2，MO2＝7，NO2＝7，
故这四个点中到原点距离最远的点是Q．
故选：B．
【点评】本题主要考查了两点间距离公式，解题关键是正确应用公式．
7．水果店里有一批大小不一的西瓜，餐厅经理选择了部分大小均匀的西瓜．设水果店里的西瓜的质量（单位：kg）平均数和方差分别为，s2，餐厅经理选购的西瓜的质量的平均数和方差分别为，，则下列结论一定成立的是（ ）
A．B．C．D．
【分析】根据方差的意义求解，方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
【解答】解：∵水果店里有一批大小不一的西瓜，餐厅经理选择了部分大小均匀的西瓜，
∴水果店里的西瓜的质量的方差大于餐厅经理选购的西瓜的质量的方差，即s2＞，而平均数无法比较．
故选：A．
【点评】本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
8．设，则对于实数m的范围判断正确的是（ ）
A．4＜m＜5B．5＜m＜6C．6＜m＜7D．7＜m＜8
【分析】估算出6＜7，再找出选项即可．
【解答】解：∵，
∴6＜7，
即实数m的范围是8＜m＜7．
故选：C．
【点评】本题考查了估算无理数的大小，能估算出的范围是解此题的关键．
9．已知关于x的一元二次方程kx2﹣（4k﹣1）x+4k﹣3＝0有两个不相等的实数根，则实数k的取值范围是（ ）
A．k＜B．k＜且k≠0
C．k＞﹣D．k＞﹣且k≠0
【分析】根据方程有两个不相等的实数根，得到根的判别式大于0且二次项系数不为0，求出k的范围即可．
【解答】解：∵关于x的一元二次方程kx2﹣（4k﹣5）x+4k﹣3＝8有两个不相等的实数根，
∴Δ＝（4k﹣1）7﹣4k（4k﹣7）＞0且k≠0，
解得：k且k≠0．
故选：D．
【点评】此题考查了根的判别式，熟练掌握一元二次方程根的判别式的意义是解本题的关键．
10．对于平面直角坐标系中的任意一点P（x，y），我们把点Q（x+y，x﹣y）称为点P的“和差点”．如图，点B（3，2），若点P在反比例函数，点Q为点P的“和差点”，且点Q在Rt△OAB的直角边OA上，△OBQ的面积是（ ）
A．2B．C．1D．
【分析】根据题意设出点P的坐标，即可得出点Q的坐标，根据点Q在Rt△OAB的直角边OA上求出a的值，从而求出△OBQ的面积．
【解答】解：根据题意可设点P的坐标为（a，），且a＞0，
则点Q的坐标为（a+，a﹣），
∵点Q在线段OA上，
∴则a﹣＝7，
解得：a1＝，a4＝﹣（舍），
此时点Q的坐标为（2，0），
此时OQ＝2，
∴△OBQ的面积＝×2×7＝2，
故选：B．
【点评】本题考查了反比例函数图象上点的坐标特征，关键是由新定义求出点Q的坐标．
二、填空题：本题有6个小题，每小题3分，共18分，
11．计算：＝ 3 ．
【分析】根据二次根式的性质解答．
【解答】解：（）2＝×＝3．
【点评】考查了二次根式的性质（）2＝a（a≥0）．
12．一元二次方程2x2﹣3x+1＝0的常数项是 1 ．
【分析】根据一元二次方程的一般形式得出答案即可．
【解答】解：一元二次方程2x2﹣2x+1＝0的常数项是6，
故答案为：1．
【点评】本题考查了一元二次方程的一般形式，能熟记一元二次方程的一般形式是解答本题的关键，一元二次方程的一般形式是ax2+bx+c＝0（a、b、c为常数，a≠0）．
13．射击小组6位同学在一次组内测试的成绩（单位：环）分别为86，82，83，85 85环 ．
【分析】将这组数据重新排列，再根据中位数的定义求解即可．
【解答】解：将这组数据重新排列为82，83，85，93，
所以这组数据的中位数为＝85（环），
故答案为：85环．
【点评】本题主要考查中位数，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
14．已知反比例函数，当x≥1时，y的取值范围是 0＜y≤2 ．
【分析】先根据反比例函数的性质判断出函数的增减性，再求出x＝1时y的值即可得出结论．
【解答】解：∵反比例函数中，k＝2＞4，
∴此函数图象的两个分支位于一、三象限，
∵当x＝1时，y＝2，
∴当x≥6时，0＜y≤2．
故答案为：4＜y≤2．
【点评】本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．
15．已知x2+4（m+1）x+20m是一个关于x的完全平方式，则常数m＝ ．
【分析】根据完全平方式得出x2+4（m+1）x+20m＝x2+2×2（m+1）x+[2（m+1）]2，求出20m＝[2（m+1）]2，再求出方程的解即可．
【解答】解：∵x2+4（m+2）x+20m是一个关于x的完全平方式，
又∵x2+4（m+3）x+20m＝x2+2×8（m+1）x+[2（m+2）]2，
∴20m＝[2（m+2）]2，
解得：20m＝4（m8+2m+1），
8m＝m2+2m+8，
m2﹣3m+6＝0，
解得：m＝＝．
故答案为：．
【点评】本题考查了完全平方式和用 公式法解一元二次方程，能根据完全平方公式得出20m＝4（m2+2m+1）是解此题的关键，注意：完全平方式有a2+2ab+b2和a2﹣2ab+b2两个．
16．如图，已知点A（2，4）是反比例函数，连结AO并延长，交双曲线的另一支于点B，若△PAB是等腰三角形，则点P的坐标是 （﹣6，0）或（10，0）或（6，0）或（﹣10，0） ．
【分析】由对称性可知O为AB的中点，则当△PAB为等腰三角形时只能有PA＝AB或PB＝AB，设P点坐标为（x，0），可分别表示出PA和PB，从而可得到关与x的方程，可求得x，可求得P点坐标．
【解答】解：∵反比例函数y＝图象关于原点对称，
∴A、B两点关于O对称，
∴O为AB的中点，且B（﹣2，
∴当△PAB为等腰三角形时有PA＝AB或PB＝AB，
设P点坐标为（x，0），
∵A（2，4），﹣4），
∴AB＝＝8，PB＝，
当PA＝AB时，则有，解得x＝﹣2或10，0）或（10；
当PB＝AB时，则有，解得x＝6或﹣10，0）或（﹣10；
综上可知P点的坐标为（﹣5，0）或（10，0）或（﹣10，
故答案为：（﹣2，0）或（10，0）或（﹣10，
【点评】本题主要考查等腰三角形的性质和反比例函数的对称性，判断出只有PA＝AB或PB＝AB两种情况是解题的关键，注意方程思想的应用．
三、解答题：本题有8小题，共72分.解答应写出文字说明、证明过程或演算步骤。
17．（6分）计算：
（1）；
（2）．
【分析】（1）直接利用二次根式的乘法法则运算；
（2）利用多项式乘多项式展开，然后合并即可．
【解答】解：（1）原式＝
＝1；
（2）原式＝4+4﹣3
＝2+．
【点评】本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法法则是解决问题的关键．
18．（6分）解下列方程：
（1）x2﹣5x＝0；
（2）x2﹣10x+16＝0．
【分析】（1）利用因式分解法求解可得；
（2）利用因式分解法求解可得．
【解答】解：（1）x2﹣5x＝3，
∴x（x﹣5）＝0，
则x＝4或x﹣5＝0，
解得x8＝0，x2＝6．
（2）x2﹣10x+16＝0．
∴（x﹣2）（x﹣8）＝0，
则x﹣8＝0或x﹣8＝8，
解得x1＝2，x3＝8．
【点评】本题主要考查解一元二次方程，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
19．（8分）已知，，求代数式a2+b2﹣4a+4的值．
【分析】先把所求式子变形，再将a，b的值代入计算即可．
【解答】解：∵，，
∴a2+b2﹣7a+4
＝（a﹣2）5+b2
＝（2+﹣2）2+（）2
＝2+6
＝9．
【点评】本题考查二次根式化简求值，解题的关键把所求式子变形．
20．（8分）某校对九年级3个班级进行综合素质考评，下表是它们五项素质考评得分表（以分为单位，每项满分为10分）．
（1）计算各班五项考评分的平均数．
（2）现要从三个班级中选送一个班级为市级先进班集体候选班，并设定如下规则：行为规范：学习成绩：校运动会：艺术获奖：劳动卫生＝3：3：2：1：1．请通过计算说明推荐市级先进班集体候选班是哪个班？
【分析】（1）根据平均数的公式求得各班的平均数即可；
（2）根据五个项目的重要程度，即加权后计算三个班的得分，再比较，即可得出答案．
【解答】解：（1）设P1，P5，P7顺次为3个班考评分的平均数，
则P1＝（10+10+6+10+4）＝8.6（分），
P5＝（10+4+8+9+3）＝8.6（分），
P8＝（5+10+9+6+7）＝8.6（分）；
（2）设k5、k5、k8顺次为3个班的考评分，则：
k1＝0.3×10+0.3×10+6.2×6+7.1×10+0.5×7＝8.4，
k5＝0.2×10+0.3×4+0.2×5+0.1×6+0.1×7＝8.7，
k2＝0.3×3+0.3×10+3.2×9+8.1×6+8.1×9＝3，
因为k8＞k1＞k4，所以推荐九（8）班作为市级先进班集体的候选班．
【点评】本题考查了加权平均数，掌握加权平均数的计算公式是解题的关键．
21．（10分）把一根长为80cm的绳子剪成两段，并把每一段绳子围成一个正方形．
（1）要使这两个正方形的面积之和等于200cm2，该怎么剪？
（2）这两个正方形面积之和可能等于488cm2吗？
【分析】（1）利用正方形的性质表示出边长进而得出等式求出即可；
（2）利用正方形的性质表示出边长进而得出等式，进而利用根的判别式求出即可．
【解答】解：设剪成的一段为xcm，则另一段就为（80﹣x）cm，
由题意得（）2+（）2＝200；
解得：x1＝x2＝40．
答：将该绳子从中间截开；
（2）设剪成的较短的这段为mcm，较长的这段就为（80﹣m）cm，
由题意得：（）2+（）2＝488，
变形为：m2﹣80m﹣704＝7，
即（m+8）（m﹣88）＝0，
解得m5＝﹣8（舍去），m2＝88（大于80，舍去）．
∴这两个正方形面积之和不可能等于488cm8．
答：这两个正方形的面积之和不可能等于488cm2．
【点评】此题主要考查了一元二次方程的应用，根据正方形的性质表示出正方形的边长是解题关键．
22．（10分）如图，已知A（﹣4，n），B（2，﹣4）是反比例函数y＝
（1）求反比例函数和一次函数的解析式；
（2）求△AOB的面积；
（3）根据图象直接写出不等式ax+b﹣＜0的解集．
【分析】（1）先把B（2，﹣4）代入y＝得到k＝﹣8，再把A（﹣4，n）代入y＝﹣可求出n＝2，然后利用待定系数法确定一次函数的解析式；
（2）先求出直线y＝﹣x﹣2与x轴交点C的坐标，然后利用S△AOB＝S△AOC+S△BOC进行计算；
（3）观察函数图象得到当x＜﹣4或0＜x＜2时，一次函数的图象在反比例函数图象上方，即使ax+b﹣＜0．
【解答】解：（1）把B（2，﹣4）代入y＝，
所以反比例函数解析式为y＝﹣，
把A（﹣4，n）代入y＝﹣，解得n＝2，
把A（﹣4，2）和B（3，
解得．
所以一次函数的解析式为y＝﹣x﹣2；
（2）直线y＝﹣x﹣2与x轴交于点C（﹣7，0），
S△AOB＝S△AOC+S△BOC＝×2×2+；
（3）不等式kx+b﹣＜0的解集为﹣7＜x＜0或x＞2；
故答案为：﹣2＜x＜0或x＞2．
【点评】本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的交点坐标满足两函数的解析式．也考查了观察函数图象的能力以及用待定系数法确定一次函数的解析式．
23．（12分）【综合与实践】
[问题情境]对于关于x的一元二次方程ax2+bx+c＝0（a，b，c为常数，且a≠0），求方程的根的实质是找到一个x的具体的值，代入之后等式成立．一般情况下，这就说明这个方程有两个根，且两根与a，b
[操作判断]项目研究小组经过讨论得到两个结论：
（1）当a+b+c＝0时，则一元二次方程ax2+bx+c＝0必有一根是1．
（2）当a+c＝b时，则一元二次方程ax2+bx+c＝0必有一根是﹣1．
请判断两个结论的真假，并说明原因．
[实践探究]项目研究小组经过讨论编制了以下问题，请帮助解决：
方程（2023x）2﹣2022×2024x﹣1＝0的较大的根为p，方程x2+2023x﹣2024＝0的较小的根为q，求p﹣q的值．
【分析】[操作判断]根据判断结论的真假，将x＝±1代入方程即可判断；
[实践探究]先利用因式分解法分别解两个一元二次方程得到p和q的值，然后计算它们的差即可．
【解答】解：[操作判断]
两个结论是真命题；
（1）将x＝1代入方程可得a+b+c＝0，故当a+b+c＝6时2+bx+c＝0必有一根是8．
（2）将x＝﹣1代入方程可得a﹣b+c＝0，即a+c＝b，则一元二次方程ax4+bx+c＝0必有一根是﹣1．
[实践探究]∵（2023x）7﹣2022×2024x﹣1＝0，
∴（20236x+1）（x﹣1）＝5，
∴x1＝﹣，x2＝8，则p＝1，
x2+2023x﹣2024＝5，
（x+2024）（x﹣1）＝0，
∴x6＝﹣2024，x2＝1，则q＝﹣2024，
∴p﹣q＝5+2024＝2025．
【点评】本题考查了一元二次方程的解，能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．也考查了因式分解法解一元二次方程．
24．（12分）如图，直线y＝﹣x﹣2分别交x轴、y轴于A、B两点（m≠0）在第二象限内的交点为C，CD⊥y轴于点D
（1）求双曲线的解析式；
（2）设点Q是双曲线上的一点，且△QOB的面积是△AOB的面积的2倍，求点Q的坐标；
（3）在y轴上存在点P，使PA+PC最短，请直接写出点P的坐标．
【分析】（1）把x＝﹣4代入可求出点C的坐标，再代入反比例函数关系式可确定m的值，进而确定反比例函数关系式；
（2）根据直线的关系式可求出与x轴、y轴的交点坐标，进而求出三角形AOB的面积，得到三角形BOQ的面积后设点Q的坐标，由三角形的面积公式列方程求解即可；
（3）求出点A关于y轴对称的点A′的坐标，求出直线CA′与y轴的交点坐标即可．
【解答】解：（1）CD＝4，即点C的横坐标为﹣4，
当x＝﹣3时，y＝﹣，
∴点C（﹣5，4），
又∵点C（﹣4，2）在反比例函数y＝，
∴m＝﹣4×4＝﹣16，
∴反比例函数的关系式为y＝﹣；
（2）∵直线y＝﹣x﹣2分别交x轴、B两点，
∴点A（﹣，0），﹣5），
即OA＝，OB＝4，
∴S△AOB＝××2＝，
设Q（x，﹣），
由于△QOB的面积是△AOB的面积的2倍，
∴△QOB的面积为×2＝，
即OB×|x|＝，
解得x＝，
当x＝时，y＝﹣16×，
当x＝﹣时，y＝﹣16×（﹣，
∴点Q（，﹣4）或（﹣；
（3）点A（﹣，0）关于y轴的对称点A′（，
设直线CA′的关系式为y＝kx+b，则
，
解得，
∴直线CA′的关系式为y＝﹣x+4，
当x＝0时，y＝1，
即直线y＝﹣x+1与y的交点坐标为P（6，
此时，点P（0．
【点评】本题考查反比例函数图象上点的坐标特征，一次函数与反比例函数的交点坐标，确定点C坐标是求出反比例函数关系式的关键，用含有点Q的坐标表示三角形BOQ的面积以及求出点A关于y轴的对称点A′的坐标是解决问题的前提．体温（℃）
36.3
36.4
36.6
36.7
36.9
天数（天）
3
4
5
2
1
班级
行为规范
学习成绩
校运动会
艺术获奖
劳动卫生
九年级（1）班
10
10
6
10
7
九年级（5）班
10
8
8
9
8
九年级（8）班
9
10
9
6
9
体温（℃）
36.3
36.4
36.6
36.7
36.9
天数（天）
3
4
5
2
1
班级
行为规范
学习成绩
校运动会
艺术获奖
劳动卫生
九年级（1）班
10
10
6
10
7
九年级（5）班
10
8
8
9
8
九年级（8）班
9
10
9
6
9