2024年甘肃省武威市凉州区金羊九年制学校联片教研中考二模数学试题（原卷版+解析版）

这是一份2024年甘肃省武威市凉州区金羊九年制学校联片教研中考二模数学试题（原卷版+解析版），文件包含2024年甘肃省武威市凉州区金羊九年制学校联片教研中考二模数学试题原卷版docx、2024年甘肃省武威市凉州区金羊九年制学校联片教研中考二模数学试题解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

一、选择题（共30分）
1. 的相反数是（ ）
A. 2B. C. D.
【答案】A
【解析】
【分析】本题主要考查了求一个数的相反数，只有符号不同的两个数互为相反数，0的相反数是0，据此求解即可．
【详解】解：的相反数是2，
故选：A．
2. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产作品录．下面四幅作品分别代表“惊蛰”、“谷雨”、“立秋”、“冬至”，其中是轴对称图形的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题考查了轴对称图形的概念，根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【详解】A、C、D选项中的图形都不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
B选项中的图形能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：B．
3. 下列去括号正确是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查去括号的方法：去括号时，运用乘法的分配律，先把括号前的数字与括号里各项相乘，再运用括号前是“”，去括号后，括号里的各项都不改变符号；括号前是“”，去括号后，括号里的各项都改变符号．顺序为先大后小．
应用去括号法则逐个计算即可得到结论．
【详解】解：A．，故此选项正确；
B．，故此选项错误；
C．，故此选项错误；
D．，故此选项错误．
故选：A．
4. 若方程是关于x，y的二元一次方程，则a的值为（ ）
A. B. C. 0D. 1
【答案】D
【解析】
【分析】本题主要考查了二元一次方程的定义，含有两个未知数并且含有未知数的项的次数都是1的整式方程叫做二元一次方程．
直接根据二元一次方程的定义列方程求值即可．
【详解】解：∵是关于x，y的二元一次方程，
∴，解得：．
故选D．
5. 某校要调查七、八、九三个年级1200名学生的睡眠情况，下列抽样选取最合适的是（ ）
A. 选取该校100名七年级的学生B. 选取该校100名男生
C. 选取该校100名女生D. 随机选取该校100名学生
【答案】D
【解析】
【分析】抽样调查时要随机抽取，尽量使抽取的样本具有代表性和广泛性，由此可判断出符合题意的答案．
【详解】解：要调查七、八、九三个年级1200名学生的睡眠情况，抽样时要在1200名学生中随机抽取，不能仅限男生、女生或某年级的学生，
故答案为：D．
【点睛】本题考查抽样调查时收集数据的过程与方法，利用数据调查应具有随机性是解题的关键．
6. 一个多边形的内角和与它的外角和相等，则这个多边形的边数为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】多边形的内角和公式（n-2）·180°，多边形外角和为360°，由此列方程即可解答．
【详解】解：设多边形的边数为，根据题意，得：
，
解得．
故选C．
【点睛】本题考查多边形的内角和与外角和，熟记内角和公式和外角和为60°是解答的关键．
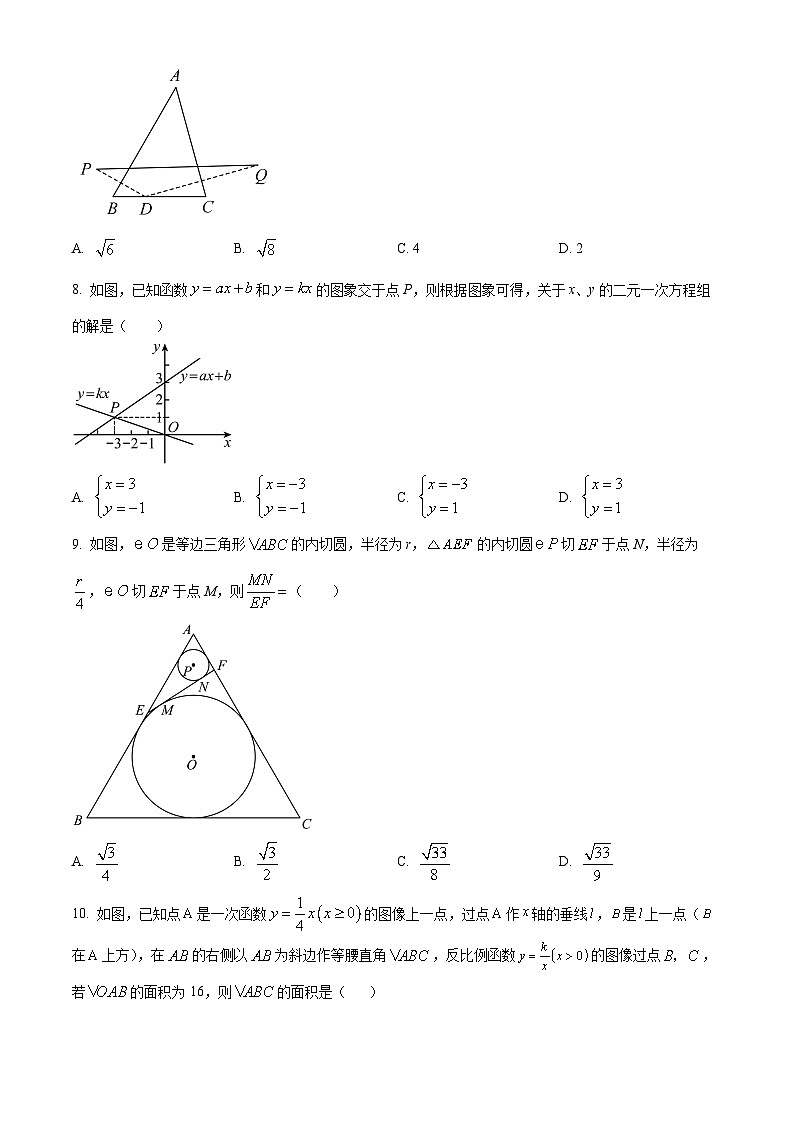
7. 如图，在中，，，，点为上一点，点分别是点关于的对称点，则的最小值是（ ）
A. B. C. 4D. 2
【答案】A
【解析】
【分析】连接，由轴对称的性质得到，，得到，，则是等腰直角三角形，得到，当取得最小值时，则,此时取得最小值，求出，即可得到的最小值．
【详解】解：连接，
∵点分别是点关于的对称点，
∴，，
∴，，
∴是等腰直角三角形，
∴，
∵点为上一点，
∴当取得最小值时，则,此时取得最小值，
当时，，
∵，
∴，
∴，
∴，
∴，
∴的最小值为，
故选：A
【点睛】此题考查了轴对称的性质、直角三角形的性质、勾股定理、等腰三角形的判定和性质等知识，证明是解题的关键．
8. 如图，已知函数和的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查一次函数与二元一次方程组，解题的关键是明确题意，利用数形结合的思想解答问题．根据函数图象可以得到两个函数交点坐标，从而可以得到两个函数联立的二元一次方程组的解．
【详解】解：根据函数图象可知，
函数和的图象交于点的坐标是，
故关于，的二元一次方程组的解是，
故选：C
9. 如图，是等边三角形的内切圆，半径为r，的内切圆切于点N，半径为，切于点M，则（ ）

A. B. C. D.
【答案】D
【解析】
【分析】利用切线长的关系求出，构造矩形，则，把放在中运用勾股定理，特殊角的三角函数等求，再求比值．
【详解】解：设与、的切点分别是Q、G、与、的切点分别是是T、S、连接、、、，,,
过点O作，交得延长线于点H，
则四边形是矩形，
∴，，，，，
∵，，
∴是角平分线，
∵，，
∴P在上，
∵等边三角形，
∴，
中，，，
∴①，
中，，，
∴②，
得，
∴，
中，
，
，
∴,
∴,
∴，

故选：D．
【点睛】本题考查了切线长定理，切线的性质定理，勾股定理，特殊角的三角函数值，矩形的判定和性质，等边三角形的性质，熟练掌握特殊切线长定理，勾股定理，特殊角的三角函数，等边三角形的性质是解题的关键．
10. 如图，已知点是一次函数的图像上一点，过点作轴的垂线，是上一点（在上方），在的右侧以为斜边作等腰直角，反比例函数的图像过点，若的面积为16，则的面积是（ ）
A. 3B. 4C. 6D. 12
【答案】D
【解析】
【分析】本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积等知识，过作轴于，交于，设，根据直角三角形斜边中线是斜边一半得：，设，则，，因为、都在反比例函数的图象上，列方程可得结论，熟练掌握反比例函数上的点符合反比例函数的关系式是关键．
【详解】解：过作轴于，交于，如图所示：
轴，
，
是等腰直角三角形，
，
设，则，
设，则，，
，在反比例函数的图象上，
，解得，
，
，
，
，
．
故选：D．
二、填空题（共24分）
11. 单项式的系数是__________．
【答案】
【解析】
【分析】本题考查了单项式的概念，单项式中的数字因数叫做单项式的的系数，系数包括它前面的符号，单项式的次数是所有字母的指数的和．根据系数的定义解答即可．
【详解】解：单项式的系数是．
故答案为：．
12. 若关于的方程的解为负数， 则的取值范围是________．
【答案】
【解析】
【分析】本题考查了解一元一次方程，解一元一次不等式，先解方程得出，再结合题意得出，解不等式即可得出答案．
【详解】解：移项得：，
合并同类项得：，
关于的方程的解为负数，
，
解得：，
故答案为：．
13. 如图，在中，，按以下步骤作图：①以为圆心，以任意长为半径作弧，分别交，于点，；②分别以，为圆心，以大于的长为半径作弧，两弧在内交于点；③作射线，交于点．若，，则线段的长为_______．
【答案】4
【解析】
【分析】本题考查了作图基本作图：熟练掌握基本作图（作已知角的角平分线）．也考查了角平分线的性质．
首先根据求出，然后根据角平分线的性质求解即可．
【详解】如图所示，过D点作于E，
∵
∴，即
解得
由作图可得，平分
∵，
∴．
故答案为：4．
14. 分解因式： ________．
【答案】
【解析】
【分析】直接利用平方差公式进行分解因式即可．
【详解】解：，
故答案为：．
【点睛】本题考查了利用平方差公式进行因式分解，熟练掌握平方差公式是解题的关键．
15. 若分式有意义，则x应满足的条件是______．
【答案】
【解析】
【分析】本题考查的是分式有意义的条件，根据分式有意义的条件是分母不等于零列出不等式，解不等式得到答案．
【详解】由题意得：，
解得：，
故答案为：．
16. 如图，四边形是正方形，边长为2，点E，F分别是，上的动点，且，则的最小值为____________．
【答案】
【解析】
【分析】作点A关于的对称点，连接，，，首先证明出，得到，进而得到当点，F，D三点共线时，有最小值，即的长度，然后利用勾股定理求解即可．
【详解】如图所示，．作点A关于的对称点，连接，，，
∵四边形是正方形，边长为2，
∴，
∵
∴
∴
∴
∴当点，F，D三点共线时，有最小值，即的长度
∵，，
∴．
∴的最小值为．
故答案为：．
【点睛】此题考查了正方形的性质，勾股定理，轴对称最短路径问题，全等三角形的性质和判定，解题的关键是得到当点，F，D三点共线时，有最小值，即的长度．
17. 如图，在中，，，以点A为圆心，长为半径画弧，以点B为圆心，长为半径画圆弧，若，则图中阴影部分图形的面积和为________（结果保留π）．
【答案】π
【解析】
【分析】根据题意和图形可知阴影部分的面积．
【详解】解：在，，，，
∴，即，
∵，
∴，
∴阴影部分的面积，
故答案为：π．
【点睛】本题考查扇形面积的计算、含角的直角三角形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
18. 如图，在平行四边形中，以C为位似中心，作平行四边形的位似平行四边形，且与原图形的位似比为2∶3，连接，若平行四边形的面积为20，则与的面积之和为______．
【答案】10
【解析】
【分析】本题主要考查了位似图形的性质；
根据位似图形的性质可得，，根据等高的三角形的面积比等于底边之比可得，，结合平行四边形的面积为20计算即可．
【详解】解：如图，连接，
∵平行四边形和平行四边形是位似图形，且位似比为2∶3，
∴，，
∴，，
∴，，
∴，
∴，
故答案为：10．
三、计算题（共8分）
19. （1）解不等式，并将解集在数轴上表示出来：
（2）计算：．
【答案】（1），表示解集见解析；（2）
【解析】
【分析】本题主要考查解一元一次不等式，实数的混合运算，解题的关键是掌握解一元一次不等式的基本步骤：去分母、去括号、移项、合并同类项、系数化为1．
（1）不等式去分母，去括号，移项合并，把x系数化为1，即可求出解；
（2）根据零指数幂，有理数的乘方，负整数指数幂的运算法则，代入特殊角的三角函数值，分别进行计算，然后根据实数的运算法则求得计算结果即可得答案．
【详解】（1）
去分母得，
去括号得，
移项，合并同类项得，
系数化为1得，，
数轴表示如下：
；
（2）
．
四、作图题（共6分）
20. 如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点，的顶点在格点上，请仅用无刻度的直尺在给定网格中画图，保留连线的痕迹，按步骤完成下列问题：
（1）如图1，已知点、A、均在格点上，求作点A关于直线对称点，连结；
（2）如图2.的顶点均在格点上，格点是边上一点，请在线段上找一点，连结，使；
（3）如图3.的顶点均在格点上，求作点关于直线的对称点．
【答案】（1）见解析 （2）见解析
（3）见解析
【解析】
【分析】本题主要考查了网格作图，熟练掌握轴对称性质，相似三角形的判定和性质，平行线分线段成比例，全等三角形的判定和性质等，将知识融入到作图过程中，是解题的关键．
（1）根据轴对称的性质结合网格特点作图即可；
（2）取格点G、H，连接与交于点F，由可得，则，然后可得，则此时；
（3）取格点S、T、K，构造，与交于点L，根据全等三角形的性质可得，根据网格作，延长交于，则，由可得，即点与点Q关于直线对称．
【小问1详解】
如图，将点A向上平移3个单位到上，再向右平移3个单位，即得；
【小问2详解】
如图，在过B，D的水平格线上取格点G，H，使，，连接交于点F，连接即是；
【小问3详解】
如图，取格点S、T、K，使，，将边向右平移3个单位得到线段，连接并延长交于点，点就是所求作．
五、解答题（共52分）
21. 如图，中，，垂足为D，点E、F、G分别是中点，直线交点G．
（1）求证：四边形是菱形；
（2）若，求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】（1）由直角三角形的性质可得，，可得，即可得结论；
（2）通过证明是等边三角形，可得，即可求解．
【小问1详解】
证明：∵，
∴，
∵点E、G分别是的中点，
∴，，
∴，
∴四边形是菱形；
【小问2详解】
解：∵四边形是菱形，
∴，
∵，
∴，
又∵，
∴，
∴，
∴是等边三角形，
∴，
∴．
【点睛】此题考查了直角三角形的性质、等边三角形的判定和性质、等腰三角形的性质、菱形的判定和性质等知识，熟练掌握直角三角形的性质是解题的关键．
22. 参加一次商品交易会的两家公司之间都签订了一份合同，所有公司共签订了45份合同，共有多少家公司参加商品交易会？
【答案】10．
【解析】
【详解】试题分析：设共有x家公司参加商品交易会，就可以得出有份合同，根据总共有45份合同建立方程，求出其解即可．
试题解析：设共有x家公司参加商品交易会，由题意得：，解得：，（舍去）．
答：共有10家公司参加商品交易会．
考点：一元二次方程的应用．
23. 把长为的线段任意分成3条线段，求这3条线段能够构成一个三角形的3条边的概率．
【答案】
【解析】
【分析】
【详解】解 设其中两条线段的长为，则第3条线段的长为，于是的取值范围是
①
要使3条线段构成一个三角形的3条边，其充要条件是其中任意一条线段的长度小于其余两条线段的长度之和．这等价于每条线段的长度都小于，即
②
将视为平面直角坐标系的坐标，则满足条件①的点在以为顶点的内．
而满足条件②的点在以为顶点的内，故所求概率为．
答：3条线段能构成一个三角形的三边的概率为．
24. 据统计，2020年底某市汽车拥有量为75万辆，而截止到2022年底，该市的汽车拥有量已达108万辆．为了保护环境，缓解汽车拥堵，该市拟控制汽车总量，要求到2024年底全市汽车拥有量不超过125.48万辆；且从2023年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的．假设每年新增汽车数量相同，请估算出该市从2023年初起每年新增汽车数量最多不超过多少万辆，并求出2020年底至2022年底该市汽车拥有量的年平均增长率．
【答案】从2023年初起每年新增汽车数量最多不超过20万辆；2020年底至2022年底该市汽车拥有量年平均增长率是
【解析】
【分析】设2020年底至2022年底该市汽车拥有量的年平均增长率是x，由题意可列一元二次方程求解；根据2024年底全市汽车拥有量不超过125.48万辆即可求出从2023年初起每年新增汽车数量最多不超过多少万辆．
【详解】设2020年底至2022年底该市汽车拥有量的年平均增长率是，
根据题意，得，
得，（不合题意，舍去），
设从2023年初起每年新增汽车数量最多不超过万辆，
由题意得：，解得，
答：从2023年初起每年新增汽车数量最多不超过20万辆；2020年底至2022年底该市汽车拥有量的年平均增长率是．
【点睛】本题考查一元二次方程与增长率问题．正确理解题意是解题关键．
25. 如图，是的直径，点，均在上，，弦，求的直径．

【答案】
【解析】
【分析】本题考查的是圆周角定理，含30度角的直角三角形的性质；先求得，利用度的角所对的边是斜边的一半进行计算．
【详解】解：是的直径，
．
同弧所对的圆周角相等，
．
，
．
的直径为．
26. 如图，在中，，是的中点，以为直径作，交边于点，连接，．
（1）求证；是的切线；
（2）若是的切线，，求的长．
【答案】（1）见解析 （2）
【解析】
【分析】本题是圆的综合问题，考查了圆的切线的判定与性质，勾股定理，等腰三角形的性质，掌握这些性质是解决本题的关键．
（1）要证明是的切线，只要证明即可；
（2）连接，根据等腰三角形的性质求得的长，再求的长，根据切线的性质求得，最后利用勾股定理求出的长．
【小问1详解】
证明：，是的中点，
，
又是直径，
是的切线；
【小问2详解】
连接，
点是的中点，，，
，
∴，
∴，
是的切线，
∴，
在中，由勾股定理，得，
．
27. 如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．
【答案】5米
【解析】
【详解】解：∵小刚身高1.6米，测得其影长为2.4米，∴由相似得，8米高旗杆DE的影子为：12米．
∵测得EG的长为3米，HF的长为1米，∴GH=12－3－1=8（米）．∴GM=MH=4米．，
∵MN=2米，∴．
设小桥所在圆的半径为r米，
∴，解得：r=5．
答：小桥所在圆的半径为5米．
由已知根据根据得出旗杆高度，从而得出GM=MH，再利用勾股定理求出半径即可．
28. 如图1，在平面直角坐标系中，O为坐标原点，抛物线与x轴负半轴交于点B，与x轴正半轴于点，交y轴于点C，连接，．
（1）求抛物线的解析式：
（2）如图2，点P为第三象限抛物线上一点，连接，，若设的面积为S，点P的横坐标为t，求S与t的函数关系式（不要求写出自变量t的取值范围）；
（3）在（2）的条件下，如图3，过点P作轴于点E，点K为抛物线的顶点，连接交于点F，点D为上一点，，连接，若，求点P的坐标．
【答案】（1）
（2）
（3）
【解析】
【分析】（1）先求出点C的坐标，然后用待定系数法求出函数的解析式即可；
（2）先求出，得出，过点P作轴于点L，得出，然后根据三角形面积公式求出结果即可；
（3）根据二次函数的性质求出，过点K作于点M，交于点N，作于点G，证明，得出，，过点F作于T，证明与都是等腰直角三角形，得出，，，根据，得出，求出t即可得出答案．
【小问1详解】
解：∵抛物线与轴正半轴于点，
∴，
∵在中， ，
∴，
∴
把点、代入得：
解得
∴抛物线解析式为．
【小问2详解】
解：当时，
解得：，
∴，
∴，
∵点P在抛物线上，点P的横坐标为，
∴，
过点P作轴于点L，
∴，
∴．
【小问3详解】
解：∵，
∴，
过点K作于点M，交于点N，作于点G，
根据对称性可知：，， ，
∵，
∴，
∴，
设，
∴，
∵，
∴，
∴
，
∴，
∴，
过点D作，
∵，，，
∴，
∴，，
过点F作于T，
∵，
∴与都是等腰直角三角形，
∴，，，
∵，，
∴
∵点P的横坐标为t，
∴，
∴，
∴，
∴，
解得：，
，
∴．
【点睛】本题主要考查了二次函数的综合应用，求二次函数解析式，三角形全等的判定和性质，等腰三角形的性质，平行线的判定和性质，解题的关键是作出辅助线，数形结合．