2024年陕西省西安市碑林区铁一中学中考数学四模试卷

这是一份2024年陕西省西安市碑林区铁一中学中考数学四模试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．2的相反数是（ ）
A．B．C．﹣2D．2
2．如图，直线a∥b，直线l分别交直线a、b于A，B两点，点C在直线b上，且AC＝BC，若∠2＝34°，则∠1的度数为（ ）
A．112°B．102°C．101°D．117°
3．下列运算正确的是（ ）
A．（a+b）2＝a2+b2
B．6a4b5÷（﹣3a2b5）＝﹣2a4b2
C．（2a2b3）3＝6a6b9
D．3a2b•（﹣2a3b2）＝﹣6a6b3
4．如图，直线y＝ax+b经过A，B两点，直线y＝cx+d经过C，D两点，则a，b，c，d从小到大的排列顺序为（ ）
A．a＜c＜d＜bB．c＜a＜d＜bC．a＜c＜b＜dD．c＜a＜b＜d
5．如图，在△ABC中，AC＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为（ ）
A．B．2C．D．3
6．如图，在△ABC中，AB＝AC＝5，BC＝6，AD⊥BC于D点，F边BC上一动点，过F作EF⊥CB交CA的延长线于点E，当四边形ADFE的面积与△ABC的面积相等时，DF的长度为（ ）
A．B．C．D．
7．如图，点B，C在⊙O上，点A在⊙O内，∠A＝∠B＝60°，AB＝6，BC＝10，⊙O的半径长为（ ）
A．2B．5C．D．
8．在平面直角坐标系中，若抛物线y＝x2+bx+c与x轴只有一个公共点，且过点A（m，n），B（m﹣12，n），则n的值为（ ）
A．48B．36C．24D．12
二、填空题（共5小题）
9．比较大小， （”＜”，“＞”或“＝”）．
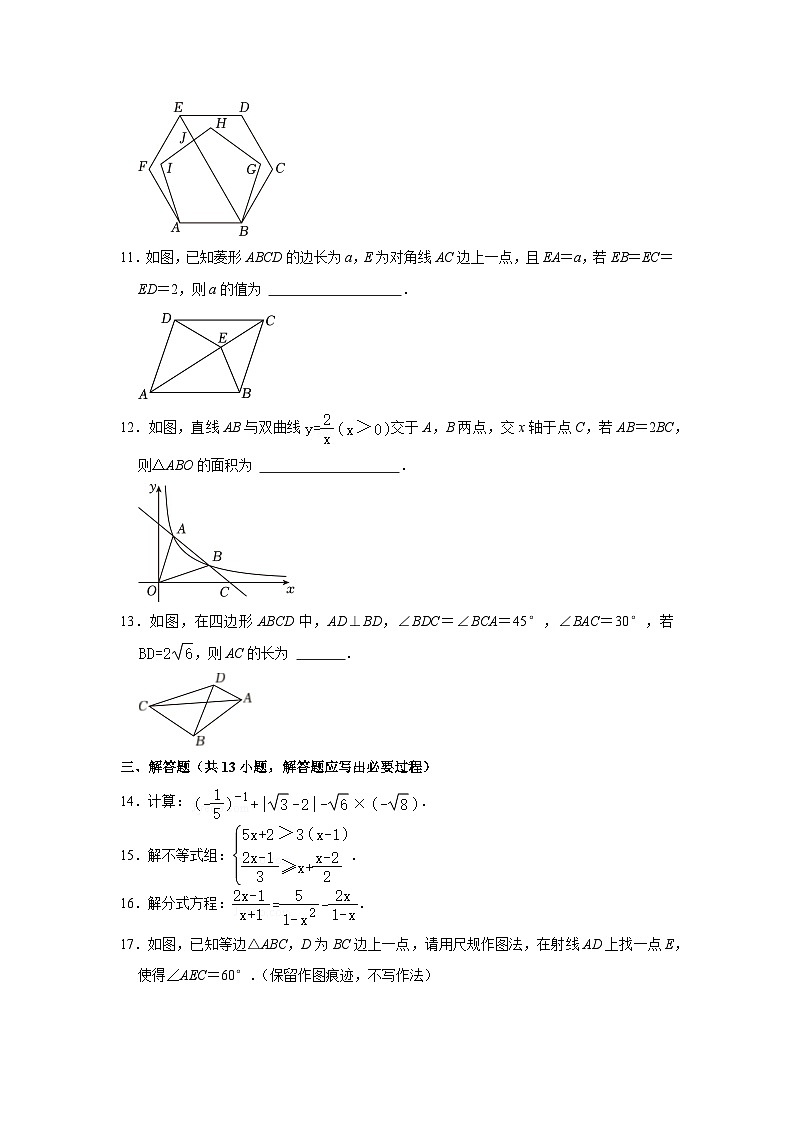
10．把边长相等的正五边形ABGH和正六边形ABCDEF的边AB重合，按照如图的方式叠放在一起，连接EB、交H于点X，则∠BKH的大小为 ．
11．如图，已知菱形ABCD的边长为a，E为对角线AC边上一点，且EA＝a，若EB＝EC＝ED＝2，则a的值为 ．
12．如图，直线AB与双曲线交于A，B两点，交x轴于点C，若AB＝2BC，则△ABO的面积为 ．
13．如图，在四边形ABCD中，AD⊥BD，∠BDC＝∠BCA＝45°，∠BAC＝30°，若，则AC的长为 ．
三、解答题（共13小题，解答题应写出必要过程）
14．计算：．
15．解不等式组：．
16．解分式方程：．
17．如图，已知等边△ABC，D为BC边上一点，请用尺规作图法，在射线AD上找一点E，使得∠AEC＝60°．（保留作图痕迹，不写作法）
18．如图，在平行四边形ABCD中，点E为BC边的中点，DF⊥AE于点F，G为DF的中点，分别延长AE，DC交于点H，求证：CG⊥DF．
19．在一个不透明的袋子中装有2个红球、2个白球，这些球除颜色外都相同．
（1）从袋子中随机摸出1个球，则摸出的这个球是红球的概率为 ．
（2）从袋子中随机摸出1个球，不放回，再随机摸出1个球，请利用列表法或画树状图的方法，求两次摸出的球都是白球的概率．
20．我国古代数学著作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步．问：人与车各几何？”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少？
21．某校组织全校学生进行了一场数学竞赛，根据竞赛结果，随机抽取了若干名学生的成绩（得分均为正整数，满分为100分，大于80分的为优秀）进行统计，绘制了如图所示尚不完整的统计图表．
数学竞赛成绩频数统计表
请结合图表解决下列问题：
（1）请将频数分布直方图补充完整；
（2）抽取的若干名学生竞赛成绩的中位数落在 组；
（3）若该校共有1500名学生，请估计本次数学竞赛成绩为“优秀”的学生人数．
22．小明与小亮要测量一建筑物CE的高度，如图，小明在点A处测得此建筑物最高点C的仰角∠CAE＝45°，再沿正对建筑物方向前进10m到达B处（即AB＝10m），测得最高点C的仰角∠CBE＝53°，小亮在点G处竖立标杆FG，当小亮的所在位置点D，标杆顶F，最高点C在一条直线上时，测得FG＝1.5m，GD＝2m．
（1）求此建筑物的高度CE；
（2）求小亮与建筑物CE之间的距离ED．
（注：结果精确到1m，参考数据：sin53°≈0.80，cs53°≈0.60，tan53°≈）
23．一种单肩包，其背带由双层部分、单层部分和调节扣构成．小华购买时，售货员演示通过调节扣加长或缩短单层部分的长度，可以使背带的长度（单层部分与双层部分长度相同，其中调节扣所占长度忽略不计）加长或缩短，设双层部分的长度为x厘米，单层部分的长度为y厘米，经测量，得到下表中数据：
（1）根据表中数据规律，求y与x的函数关系式；
（2）按小华的身高和习惯，背带的长度调为130cm时为最佳，请计算此时双层部分的长度．
24．如图，在△ABC中，BE平分∠ABC，交AC于点F，交△ABC外接圆⊙O于点E，过点E作⊙O的切线交BC延长线上点D．
（1）求证：AC∥DE；
（2）若CE＝6，DE＝8，求AF的长．
25．公园里，一个圆形喷水池的中央竖直安装一个柱形喷水装置OA，喷水口A距离水面的距离OA＝1.25米，喷出的水流在各个方向沿形状相同的抛物线路径落下．为了方便研究，以O为坐标原点，OA方向为y轴正方向，建立如图所示的坐标系．测得喷出的水流在离OA水平距离为0.75米的B处达到距水面的最大高度，同时经过距OA水平距离为2米，距水面的高度为0.75米的C点．
（1）若不计其它因素，那么水池的半径至少要多少米，才能使喷出的水流不至于落到池外？
（2）如果水流喷出的抛物线形状与（1）相同，水池的半径为3米，要使水流不落到池外，此时水流的最大高度应达到多少米？
26．提出问题 如图①，⊙O与∠ABC的两边BA，BC相切于点P，Q，则BP，BQ的数量关系为 ．
探究问题 如图②，矩形ABCD的边，AB＝3，点P在AD上，连接BP，CP，求∠BPC的最大值．
问题解决 如图③，小明和小亮在学习圆的相关知识后进行了如下的探究活动：先在桌面上固定一根笔直的木条AB，让一圆盘在木条AB上做无滑动的滚动，将一根弹性良好的橡皮筋的两端固定在木条AB的两端点处，再紧绷在圆盘边上，此时，AC，BD，AB分别与圆盘相切于点C，D，E，当圆盘滚动时橡皮筋也随之伸缩变化（即AC+CD+DB的长度会发生变化）．已知，圆盘直径为4dm，请你帮助小明和小亮探究AC+CD+DB的长度是否存在最小值？若存在，求出最小值；若不存在，请说明理由．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/4/24 16:29:44；用户：尤桂林；邮箱：18778546280；学号：47057611组别
频数
频率
A组（60.5～70.5）
a
0.3
B组（70.5～80.5）
30
0.15
C组（80.5～90.5）
50
b
D组（90.5～100.5）
60
0.3
双层部分长度x（cm）
2
8
14
20
单层部分长度y（cm）
148
136
124
112