

2023-2024学年甘肃省武威十一中教研联片七年级(下)期中数学试卷
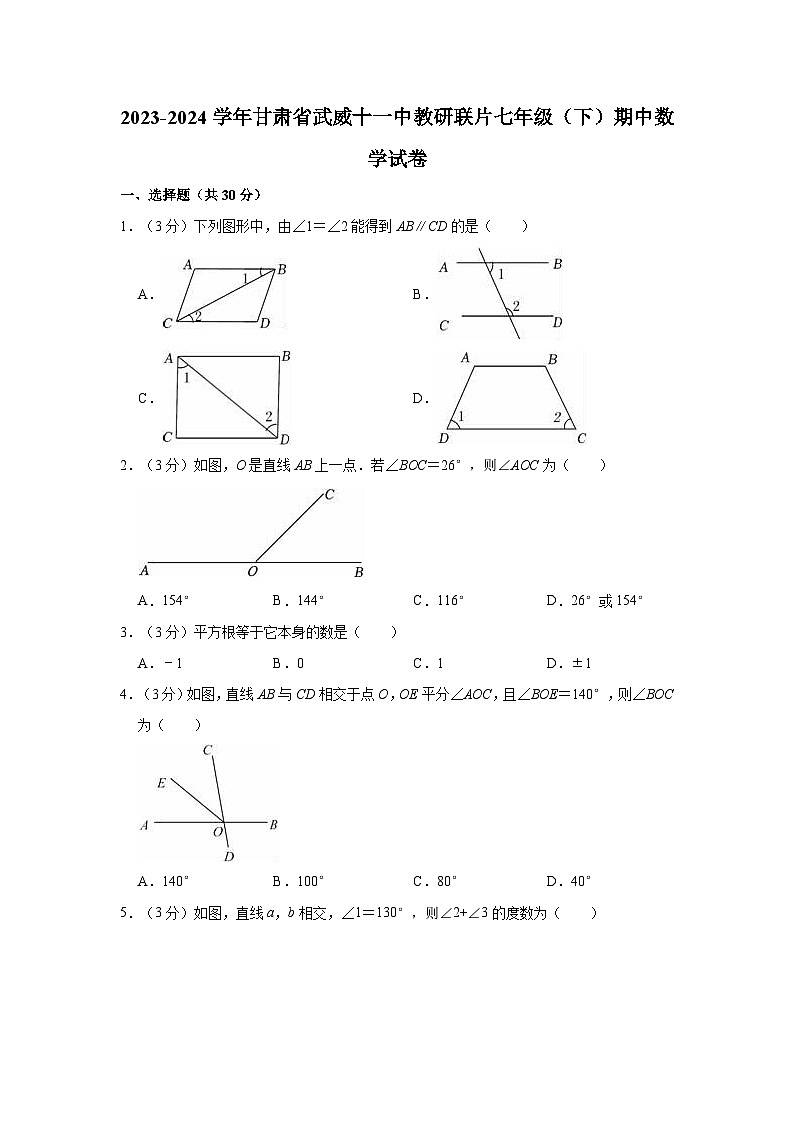
展开1.(3分)下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.B.
C.D.
2.(3分)如图,O是直线AB上一点.若∠BOC=26°,则∠AOC为( )
A.154°B.144°C.116°D.26°或154°
3.(3分)平方根等于它本身的数是( )
A.﹣1B.0C.1D.±1
4.(3分)如图,直线AB与CD相交于点O,OE平分∠AOC,且∠BOE=140°,则∠BOC为( )
A.140°B.100°C.80°D.40°
5.(3分)如图,直线a,b相交,∠1=130°,则∠2+∠3的度数为( )
A.50°B.100°C.25°D.130°
6.(3分)如图,∠3的同旁内角是( )
A.∠1B.∠2C.∠4D.∠1和∠4
7.(3分)在平面直角坐标系中,点(m,n)位于第三象限,则( )
A.m<nB.m>nC.mn>0D.m+n>0
8.(3分)下列五个命题:
①如果两个数的绝对值相等,那么这两个数的平方相等;
②内错角相等;
③在同一平面内,垂直于同一条直线的两条直线互相平行;
④两个无理数的和一定是无理数;
⑤坐标平面内的点与有序数对是一一对应的.
其中真命题的个数是( )
A.2个B.3个C.4个D.5个
9.(3分)在﹣2,,,3.14,,,这6个数中,无理数共有( )
A.4个B.3个C.2个D.1个
10.(3分)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→⋅⋅⋅根据这个规律,第2023个点的坐标为( )
A.(45,1)B.(45,2)C.(45,3)D.(45,4)
二、填空题(共24分)
11.(3分)比较大小: 6.
12.(3分)已知:若≈1.910,≈6.042,则≈ .
13.(3分)﹣125的立方根是 .
14.(3分)如图,一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上),若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α度(0<α<180),当边DE与△ABC的某一边平行时,相应的旋转角α的值为 .
15.(3分)把命题“对顶角相等”改写成“如果…那么…”的形式: .
16.(3分)如图,AB∥CD,∠ABE=120°,PE⊥CD于E,则∠PEB的度数是 度.
17.(3分)点A(3,a+1)在x轴上,点B(b﹣2,5)在y轴上,则ab的值为 .
18.(3分)中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果“帅”的坐标是(0,1),“卒”的坐标是(2,2),那么“马”的坐标是 .
三、计算题(共12分)
19.(12分)计算:
(1);
(2);
(3).
四、作图题(共5分)
20.(5分)如图,在平面直角坐标系中,点A、B、C的坐标分别为A(2,﹣1),B(4,3),C(1,2),将△ABC先向左5个单位,再向下平移3个单位得到△A1B1C1.
(1)请在图中画出△A1B1C1;
(2)写出平移后的△A1B1C1三个顶点的坐标;
A1( , ),B1( , ),C1( , ).
五、解答题(共49分)
21.(6分)已知一个正数的两个平方根分别是2a+1和a﹣4,又b﹣4的立方根为﹣2.
(1)求a,b的值;
(2)求5a﹣b的算术平方根.
22.(6分)若,求3x﹣6y的立方根.
23.(6分)如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.
24.(6分)如图,已知∠COF+∠C=180°,∠C=∠B.说明AB∥EF的理由.
25.(7分)如图,已知AE∥BC,且AE平分∠DAC,试说明∠B=∠C.
26.(8分)已知点A(3a﹣9,2a﹣10),解答下列问题:
(1)若点B的坐标为(4,5),且AB∥y轴,求a的值;
(2)若点A在第四象限,且a是整数,求点A的坐标.
27.(10分)如图所示,点A坐标(1,0),点B在y轴上,将△OAB沿x轴负方向平移,平移后的图形为△DEC,且点C的坐标为(﹣3,2).
(1)请直接写出D点,E点的坐标 , .
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题,并说明你的理由.
①求点P在运动过程中的坐标(用含t的式子表示).
②当t为多少秒时,点P的横坐标与纵坐标互为相反数.
2023-2024学年甘肃省武威十一中教研联片七年级(下)期中数学试卷
参考答案与试题解析
一、选择题(共30分)
1.【分析】在三线八角的前提下,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此判断即可.
【解答】解:A、∠1=∠2,AB∥CD,符合题意;
B、∠1+∠2=180°,AB∥CD,不符合题意;
C、∠1=∠2,得不出AB∥CD,不符合题意;
D、∠1=∠2,得不出AB∥CD,不符合题意;
故选:A.
【点评】本题考查了平行线的判定,解题的关键是注意平行线判定的前提条件必须是三线八角.
2.【分析】根据邻补角的定义可知,∠AOC=180°﹣∠BOC,据此计算即可.
【解答】解:∵O是直线AB上一点,∠BOC26°,
∴∠AOC=180°﹣∠BOC=180°﹣26°=154°.
故选:A.
【点评】本题主要考查了邻补角的运用,解决问题的关键是掌握邻补角的性质:邻补角互补,即和为180°.
3.【分析】根据平方根的性质计算.
【解答】解:平方根等于它本身的数是0.
故选:B.
【点评】本题考查了平方根:如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.
4.【分析】根据平角的意义求出∠AOE,再根据角平分线的定义得出∠AOE=∠COE,由角的和差关系可得答案.
【解答】解:∵∠AOE+∠BOE=180°,
∴∠AOE=180°﹣∠BOE=180°﹣140°=40°,
又∵OE平分∠AOC,
∴∠AOE=∠COE=40°,
∴∠BOC=∠BOE﹣∠COE
=140°﹣40°
=100°,
故选:B.
【点评】本题考查角平分线的定义,邻补角,掌握角平分线、邻补角的意义以及图形中角的和差关系是正确解答的关键.
5.【分析】根据图形以及∠1=130°,可求出∠2和∠3的值,进而能得出∠2+∠3的值.
【解答】解:由图形可得:∠2=∠3=180°﹣∠1=50°,
∴∠2+∠3=100°.
故选:B.
【点评】本题考查了邻补角和对顶角的知识,比较简单,注意在计算角度时不要出错.
6.【分析】根据同旁内角的定义判断即可.
【解答】解:∠1和∠4都是∠3的同旁内角,
故选:D.
【点评】本题考查了同旁内角的定义,熟练掌握这个定义是解题的关键.
7.【分析】根据第三象限内点的坐标特点解答即可.
【解答】解:∵点(m,n)位于第三象限,
∴m<0,n<0,
∴mn>0.
故选:C.
【点评】本题考查的是点的坐标,熟知各象限内点的坐标特点是解题的关键.
8.【分析】根据无理数、平行线的判定和性质判断即可.
【解答】解:①如果两个数的绝对值相等,那么这两个数的平方相等,是真命题;
②两直线平行,内错角相等,原命题是假命题;
③在同一平面内,垂直于同一条直线的两条直线互相平行,是真命题;
④两个无理数的和不一定是无理数,原命题是假命题;
⑤坐标平面内的点与有序数对是一一对应的,是真命题;
故选:B.
【点评】此题主要考查了命题与定理,熟练根据无理数、平行线的判定和性质得出是解题关键.
9.【分析】要确定题目中的无理数,在明确无理数的定义的前提下,知道无理数分为3大类:π类,开方开不尽的数,无限不循环的小数,根据这3类就可以确定无理数的个数.从而得到答案.
【解答】解:根据判断无理数的3类方法,可以直接得知:
是开方开不尽的数是无理数,
属于π类是无理数,
因此无理数有2个.
故选:C.
【点评】本题考查了无理数的定义,判断无理数的方法,要求学生对无理数的概念的理解要透彻.
10.【分析】以正方形最外边上的点为准考虑,点的总个数等于最右边下角的点横坐标的平方,且横坐标为奇数时最后一个点在x轴上,为偶数时,从x轴上的点开始排列,求出与2023最接近的平方数为2025,然后写出第2023个点的坐标即可.
【解答】解:由图形可知,图中各点分别组成了正方形点阵,每个正方形点阵的整点数量依次为最右下角点横坐标的平方,
且当正方形最右下角点的横坐标为奇数时,这个点可以看作按照运动方向到达x轴,当正方形最右下角点的横坐标为偶数时,这个点可以看作按照运动方向离开x轴,
∵452=2025,
∴第2025个点在x轴上坐标为(45,0),
则第2023个点在(45,2).
故选:B.
【点评】本题为平面直角坐标系下的点坐标规律探究题,解答时除了注意点坐标的变化外,还要注意点的运动方向.
二、填空题(共24分)
11.【分析】先运用二次根式的性质把根号外的移到根号内,然后只需根据条件分析被开方数即可.
【解答】解:∵6=,
∴<,
即<6.
故答案为:<.
【点评】本题考查了实数的大小比较,注:无理数和有理数比较大小,常把有理数化成根式的形式.
12.【分析】根据被开方数扩大100倍,算术平方根扩大10倍,可得答案.
【解答】解:若≈1.910,≈6.042,则≈604.2,
故答案为:604.2.
【点评】本题考查了算术平方根,利用被开方数与算术平方根的关系是解题关键.
13.【分析】直接利用立方根的定义即可求解.
【解答】解:∵﹣5的立方等于﹣125,
∴﹣125的立方根是﹣5.
故答案为﹣5.
【点评】此题主要考查了立方根的定义,求一个数的立方根,应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.
14.【分析】分三种情形分别画出图形,利用平行线的性质一一求解即可.
【解答】解:①如图1中,当DE∥AB时,
易证∠ABD=∠D=45°,可得旋转角α=45°
②如图2中,当DE∥BC时,
易证∠ABD=∠ABC+∠CBD=∠ABC+∠D=75°,可得旋转角α=75°
③如图3中,当DE∥AC时,作BM∥AC,
则AC∥BM∥DE,
∴∠CBM=∠C=90°,∠DBM=∠D=45°,
∴∠ABD=30°+90°+45°=165°,可得旋转角α=165°,
综上所述,满足条件的旋转角α为45°或75°或165°
故答案为45°或75°或165°.
【点评】本题考查旋转变换,平行线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
15.【分析】命题中的条件是两个角是对顶角,放在“如果”的后面,结论是这两个角相等,应放在“那么”的后面.
【解答】解:题设为:两个角是对顶角,结论为:这两个角相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么这两个角相等,
故答案为:如果两个角是对顶角,那么这两个角相等.
【点评】本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.
16.【分析】根据两直线平行,同旁内角互补,即可求出∠BEC,再根据垂直的定义,求出∠CEP=90°,然后根据∠PEB=∠CEP﹣∠BEC,代入数据计算即可得解.
【解答】解:∵AB∥CD,∠ABE=120°,
∴∠BEC=180°﹣∠ABE=180°﹣120°=60°,
∵PE⊥CD,
∴∠CEP=90°,
∴∠PEB=∠CEP﹣∠BEC=90°﹣60°=30°.
故答案为:30.
【点评】本题考查了平行线的性质,垂直的定义的应用,熟记性质并准确识图是解题的关键.
17.【分析】根据x轴上点的纵坐标为0,y轴上点的横坐标为0分别列式求出a、b,再代入计算即可得解.
【解答】解:因为点A(3,a+1)在x轴上,点B(b﹣2,5)在y轴上,
所以a+1=0,b﹣2=0,
解得a=﹣1,b=2,
所以ab=(﹣1)2=1.
故答案为:1.
【点评】本题考查了点的坐标,是基础题,掌握坐标轴上点的坐标特征是解题的关键.
18.【分析】根据“帅”的坐标是(0,1),“卒”的坐标是(2,2),建立平面直角坐标系,进而得出“马”的位置.
【解答】解:∵“帅”的坐标是(0,1),“卒”的坐标是(2,2),
∴建立平面直角坐标系,如图所示,
∴“马”的位置应表示为:(﹣2,2).
故答案为:(﹣2,2).
【点评】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
三、计算题(共12分)
19.【分析】(1)利用算术平方根的定义,立方根的定义,实数运算法则计算即可;
(2)利用算术平方根的定义,立方根的定义,实数运算法则计算即可;
(3)利用算术平方根的定义,立方根的定义,二次根式的计算,实数运算法则计算即可.
【解答】解:(1)原式=5﹣3﹣1
=1;
(2)原式=﹣4+4﹣2
=﹣2;
(3)原式=3+1﹣1
=3.
【点评】本题考查了实数的混合运算,二次根式的混合运算,立方根和算术平方根等知识,掌握实数的运算法则和公式计算是关键.
四、作图题(共5分)
20.【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用(1)中所画图形得出对应点坐标.
【解答】解:(1)如图所示:△A1B1C1即为所求;
(2)A1(﹣3,﹣4),B1(﹣1,0),C1(﹣4,﹣1);
故答案为:﹣3,﹣4;﹣1,0;﹣4,﹣1.
【点评】此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.
五、解答题(共49分)
21.【分析】(1)根据平方根的性质和立方根的定义即可求得答案;
(2)将a,b的值代入5a﹣b中计算后根据算术平方根的定义即可求得答案.
【解答】解:(1)∵一个正数的两个平方根分别是2a+1和a﹣4,b﹣4的立方根为﹣2,
∴2a+1+a﹣4=0,b﹣4=﹣8,
解得:a=1,b=﹣4;
(2)∵a=1,b=﹣4,
∴5a﹣b=5×1+4=9,
∵32=9,
∴5a﹣b的算术平方根为3.
【点评】本题考查平方根,算术平方根及立方根的定义,熟练掌握相关定义是解题的关键.
22.【分析】先根据算术平方根与绝对值的非负性可得,|x2﹣9|=0,即可得2x=y,x2=9,进而可求出x、y的值,再代入3x﹣6y中,即可求解.
【解答】解:∵,
又∵,|x2﹣9|≥0,
∴,|x2﹣9|=0,
∴2x=y,x2=9,
∵x2=9,
∴x=±3,
∴或者,
当时,3x﹣6y=﹣27;
∴;
当时,3x﹣6y=27,
∴;
即3x﹣6y的立方根为3或者﹣3.
【点评】本题考查的是非负数的性质及立方根的定义,能根据非负数的性质求出x、y的值是解答此题的关键.初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)算术平方根.当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.
23.【分析】先利用平角180°减去∠AOD,求出∠BOD的度数,再根据垂直定义求出∠BOC的度数,然后进行计算即可解答.
【解答】解:∵∠AOD=130°,
∴∠BOD=180°﹣∠AOD=180°﹣130°=50°,
∵OC⊥AB,
∴∠BOC=90°,
∴∠COD=∠BOD+∠BOC=50°+90°=140°,
∴∠COD的度数为140°.
【点评】本题考查了垂线,根据题目的已知条件并结合图形分析是解题的关键.
24.【分析】根据平行线的判定可得EF∥CD,AB∥CD,再根据两条直线都和第三条直线平行,那么这两条直线平行即可求解.
【解答】解:∵∠COF+∠C=180°,
∴EF∥CD,
∵∠C=∠B,
∴AB∥CD,
∴AB∥EF.
【点评】考查了平行线的判定,关键是熟悉同旁内角互补,两直线平行;内错角相等,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行的知识点.
25.【分析】根据角平分线的定义可得∠1=∠2,再根据两直线平行,同位角相等可得∠1=∠B,两直线平行,内错角相等可得∠2=∠C,从而得到∠B=∠C,然后根据等角对等边即可得证.
【解答】证明:∵AE平分∠DAC,
∴∠1=∠2,
∵AE∥BC,
∴∠1=∠B,∠2=∠C,
∴∠B=∠C,
【点评】本题考查了平行线的性质,等腰三角形的判定,熟记性质是解题的关键.
26.【分析】(1)根据AB∥y轴,可得3a﹣9=4,求出a的值即可;
(2)根据点A在第四象限,可得3a﹣9>0,且2a﹣10<0,求出a的取值范围,根据a是整数,可得a=4,进一步可得点A坐标.
【解答】解:(1)∵点B的坐标为(4,5),且AB∥y轴,
∴3a﹣9=4,
解得a=;
(2)∵点A在第四象限,
∴3a﹣9>0,且2a﹣10<0,
解得3<a<5,
∵a是整数,
∴a=4,
∴点A的坐标为(3,﹣2).
【点评】本题考查了坐标与图形性质,熟练掌握平面直角坐标系内点的坐标特征是解题的关键.
27.【分析】(1)根据点B,C的横坐标可得平移方式为沿x轴负方向平移3个单位长度,再根据点的坐标的平移变换规律即可得;
(2)①分点P在BC上,即0≤t≤3和点P在CD上,即3<t≤5两种情况,根据运动速度和时间、以及点P的位置进行求解即可得;②分点P在BC上,即0≤t≤3和点P在CD上,即3<t≤5两种情况,分别根据点P的横坐标与纵坐标互为相反数建立方程,解方程即可得.
【解答】解:(1)∵点B的横坐标为0,点C的横坐标为﹣3,
∴平移方式为沿x轴负方向平移3个单位长度,
∵A(1,0),O(0,0),
∴D(0﹣3,0),E(1﹣3,0),
即D(﹣3,0),E(﹣2,0).
故答案为:D(﹣3,0),E(﹣2,0);
(2)①当点P在BC上时,点P的横坐标为﹣t,纵坐标为2,即P(﹣t,2),
当点P在CD上时,点P的横坐标为﹣3,纵坐标为BC+CD﹣t=5﹣t,即P(﹣3,5﹣t);
②∵C(﹣3,2),CD⊥x轴,
∴BC=3,CD=2,
∴点P运动到点C所需时间为秒,运动到点D所需时间为秒,
当点P在BC上,即0≤t≤3时,设P(﹣t,2),
∵点P的横坐标与纵坐标互为相反数,
∴﹣t+2=0,解得t=2,符合题意;
当点P在CD上,即3<t≤5时,设P(﹣3,3+2﹣t),即P(﹣3,5﹣t),
∵点P的横坐标与纵坐标互为相反数,
∴﹣3+5﹣t=0,解得t=2,不符合题意,舍去;
综上,当t=2秒时,点P的横坐标与纵坐标互为相反数.
【点评】本题考查了点的坐标的平移变换、坐标与图形等知识点,熟练掌握点的坐标的平移变换规律是解题关键.
2023-2024学年甘肃省武威二十一中联片教研七年级(下)期中数学试卷(含解析): 这是一份2023-2024学年甘肃省武威二十一中联片教研七年级(下)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年甘肃省武威十一中教研联片中考数学二模试卷(含解析): 这是一份2024年甘肃省武威十一中教研联片中考数学二模试卷(含解析),共25页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
甘肃省武威市凉州区武威二十一中联片教研2023-2024学年七年级下学期4月期中数学试题(原卷版+解析版): 这是一份甘肃省武威市凉州区武威二十一中联片教研2023-2024学年七年级下学期4月期中数学试题(原卷版+解析版),文件包含甘肃省武威市凉州区武威二十一中联片教研2023-2024学年七年级下学期4月期中数学试题原卷版docx、甘肃省武威市凉州区武威二十一中联片教研2023-2024学年七年级下学期4月期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。












