初中数学苏科版七年级下册9.5 多项式的因式分解教学设计

这是一份初中数学苏科版七年级下册9.5 多项式的因式分解教学设计，共4页。教案主要包含了探索活动，例题讲解，拓展应用，课堂小结，作业布置等内容，欢迎下载使用。
9．5 多项式的因式分解（1）
教学目标
1．了解因式分解的意义，会用提公因式法进行因式分解（指数是正整数）．
2．经历通过单项式乘多项式探索提取公因式法因式分解的过程，体会单项式乘多项式与提取公因式之间的联系，发展逆向思维的能力．
教学重点
因式分解的意义，用提公因式法分解因式．
教学难点
正确找出多项式中各项的公因式．
教学过程（教师）
学生活动
设计思路
一、探索活动
1、你能把多项式ab＋ac＋ad写成积的形式吗？
ab＋ac＋ad＝
像这样，把一个多项式写成几个整式的积的形式叫做多项式的 。
练习：下列各式由左到右的变形哪些是因式分解，哪些不是？
(1) ab＋ac＋d＝a（b＋c）＋d
(2)a2－1＝（a＋1）（a－1）
(3)（a＋1）（a－1）＝a2－1
(4)8a2b3c＝2a2·2b3·2c
(5)
（1）．学生口答；
（2）.观察、思考、归纳得出因式分解的定义
（3）.学生思考后口答
学生通过乘法分配律的逆运算（因数分解），得出因式分解的定义，通过练习加深对因式分解的理解。
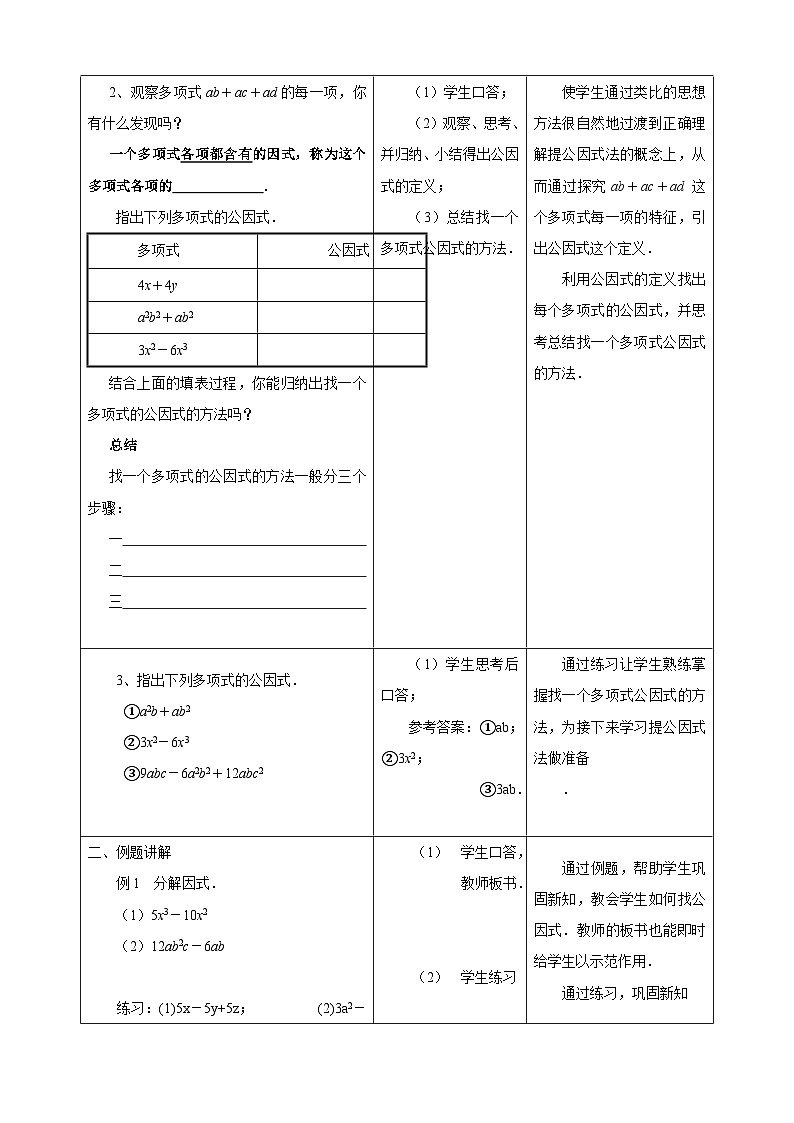
2、观察多项式ab＋ac＋ad的每一项，你有什么发现吗？
一个多项式各项都含有的因式，称为这个多项式各项的 ．
指出下列多项式的公因式．
多项式
公因式
4x＋4y

a2b2＋ab2

3x2－6x3

结合上面的填表过程，你能归纳出找一个多项式的公因式的方法吗？
总结
找一个多项式的公因式的方法一般分三个步骤：
一
二
三
（1）学生口答；
（2）观察、思考、并归纳、小结得出公因式的定义；
（3）总结找一个多项式公因式的方法．
使学生通过类比的思想方法很自然地过渡到正确理解提公因式法的概念上，从而通过探究ab＋ac＋ad 这个多项式每一项的特征，引出公因式这个定义．
利用公因式的定义找出每个多项式的公因式，并思考总结找一个多项式公因式的方法．
3、指出下列多项式的公因式．
①a2b＋ab2
②3x2－6x3
③9abc－6a2b2＋12abc2
（1）学生思考后口答；
参考答案：①ab；②3x2；
③3ab．
通过练习让学生熟练掌握找一个多项式公因式的方法，为接下来学习提公因式法做准备
．
二、例题讲解
例1 分解因式．
（1）5x3－10x2
（2）12ab2c－6ab
练习：(1)5x－5y+5z； (2)3a2－9ab；
(3)6mn－9m2n； （4）x2y－2xy2+xy
学生口答，教师板书．
学生练习
通过例题，帮助学生巩固新知，教会学生如何找公因式．教师的板书也能即时给学生以示范作用．
通过练习，巩固新知
例2 分解因式－2m3＋8m2－12m．
讲解：当多项式的第一项的系数为“－”时，先把“－”当作公因式的负号写在括号外，使括号内第一项的系数为“＋”．
练习：（1）－a+ab－ac （2）－9x2y－36xy2+3xy
（1）学生口述方法，学生可能这样分解因式：，也可能有学生分解为：
．
（2）学生练习
由教师指出规定，教会学生学会解题后的检查，检查公因式是否提取正确，检查括号内的第一项的系数是否为“＋”．
通过练习，巩固新知.
例3 把下列各式分解因式
（1）3a（x＋y）－2b（x＋y）；
（2）3a（x－y）－2b（y－x）
（3）10x(x-y)2 -15(y－x)3
练习：
（1）3a(b+c)－2(b+c)
（2）m2 (n－1)+m(1－n)
(3)2a(x－y)－4b(y－x)；
(4)(2x+y)(2x－3y)+x(2x+y)
(5) 12y(x-y)2 + 8(y-x)3
学生口答，教师板书
（2）学生练习，集体纠错
探索公因式为多项式的题型，使学生明确公因式不仅是单项式，还可以是多项式，渗透了“整体法”的思想．
通过五位同学上黑板练习，展示学生解答过程，集体纠错，提高实效．
三、拓展应用
1、 用因式分解的方法计算：
(1)；
(2)．
2、如果x+y＝0，xy＝－7，则x2y+xy2＝_____，x2+y2＝____.
学生思考，口答
通过拓展应用，让学生掌握因式分解的灵活应用，培养学生的综合应用能力．
五、课堂小结
通过今天的学习，你学会了什么？与大家分享．
因式分解与整式乘法有什么联系和区别？
区别：
整式乘法：有几个整式积的形式转化成一个多项式的形式．
因式分解：有一个多项式的形式转化成几个整式的积的形式．
联系：多项式的因式分解与整式乘法是两种相反方向的变形，它们互为逆过程．
学生思考，交流并汇报．
小结能使将所学知识条理化、系统化；让学生在交流中共享．
通过提问把学生推到思维的前沿，让学生自探数学知识，自获数学结论，自由发表见解，自主发现因式分解与整式乘法的区别与联系．在反思中提升．
六、作业布置
1．（必做题）课本习题9.5第1、2题；
2．（选做题）思考：
（1）20042＋2004能被2005整除吗？
（2）如果n是自然数，那么n2＋n是奇数还是偶数？
课后完成必做题，并根据自己的能力水平确定是否选做思考题．
设置分层作业，尊重学生的个体差异，为不同学生的发展创造不同的条件．