2023-2024学年江苏省苏州市吴江区实验初级中学八年级（下）第一次月考数学试卷（含解析）

这是一份2023-2024学年江苏省苏州市吴江区实验初级中学八年级（下）第一次月考数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.如图所示新能源车企的车标中，既是轴对称图形，又是中心对称图形的是( )
A. B.
C. D.
2.昆山市今年共约有21000名考生参加体育中考，为了了解这21000名考生的体育成绩，从中抽取了2000名考生的体育成绩进行统计分析，以下说法正确的是( )
A. 该调查方式是普查
B. 每一名考生是个体
C. 抽取的2000名考生的体育成绩是总体的一个样本
D. 样本容量是2000名考生
3.计算3aa+1+3a+1的结果是
( )
A. 3B. 3a+3C. 2D. 6aa+1
4.平行四边形的对角线长为x、y，一边长为12，则x、y的值可能是( )
A. 8和14B. 10和14C. 18和20D. 10和34
5.若a≠b，则下列分式变形正确的是
( )
A. a+1b+1=abB. a−1b−1=abC. a2b2=abD. 2a2b=ab
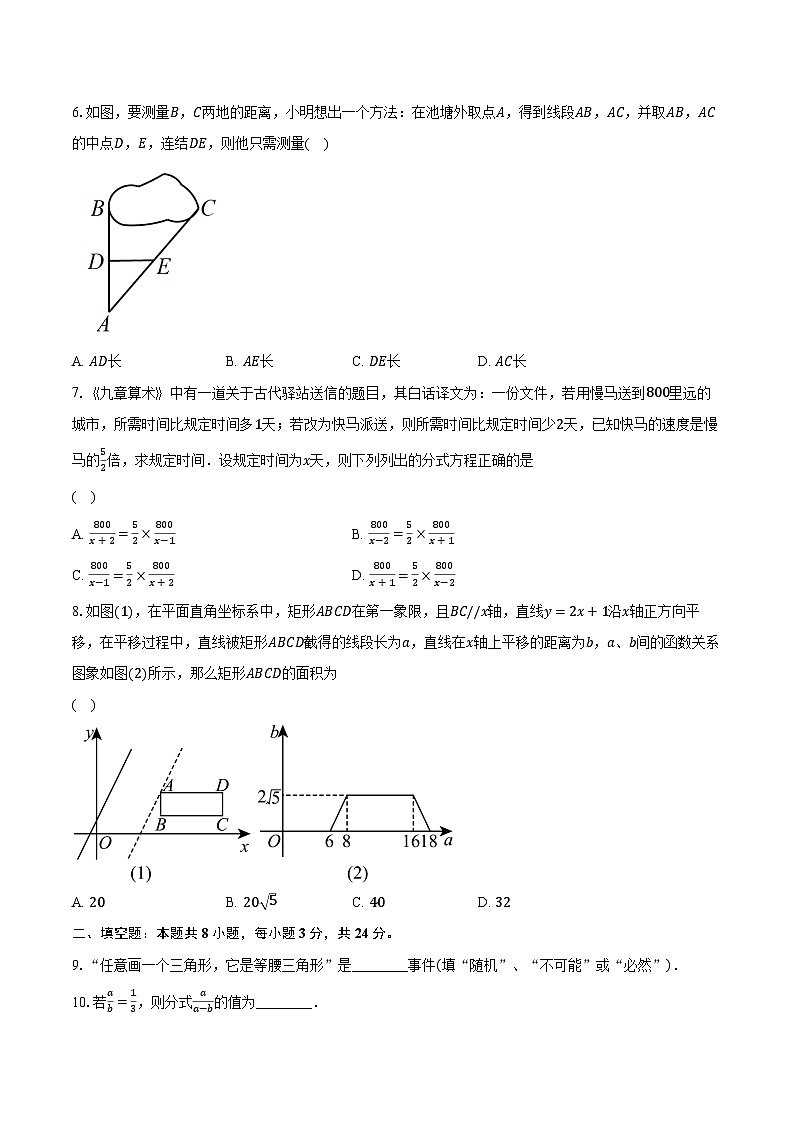
6.如图，要测量B，C两地的距离，小明想出一个方法：在池塘外取点A，得到线段AB，AC，并取AB，AC的中点D，E，连结DE，则他只需测量( )
A. AD长B. AE长C. DE长D. AC长
7.《九章算术》中有一道关于古代驿站送信的题目，其白话译文为：一份文件，若用慢马送到800里远的城市，所需时间比规定时间多1天；若改为快马派送，则所需时间比规定时间少2天，已知快马的速度是慢马的52倍，求规定时间．设规定时间为x天，则下列列出的分式方程正确的是
( )
A. 800x+2=52×800x−1B. 800x−2=52×800x+1
C. 800x−1=52×800x+2D. 800x+1=52×800x−2
8.如图(1)，在平面直角坐标系中，矩形ABCD在第一象限，且BC/​/x轴，直线y=2x+1沿x轴正方向平移，在平移过程中，直线被矩形ABCD截得的线段长为a，直线在x轴上平移的距离为b，a、b间的函数关系图象如图(2)所示，那么矩形ABCD的面积为
( )
A. 20B. 20 5C. 40D. 32
二、填空题：本题共8小题，每小题3分，共24分。
9.“任意画一个三角形，它是等腰三角形”是________事件(填“随机”、“不可能”或“必然”)．
10.若ab=13，则分式aa−b的值为________．
11.某样本容量是60，分组后，第2组的频率是0.15，那么第2组的频数是_________．
12.若分式x−1x−1的值为0，则x=_____．
13.已知x−1x=3，则x2+1x2=______．
14.四边形具有不稳定性．如图，矩形ABCD按箭头方向变形成平行四边形A′B′C′D′，变形后∠A′=30∘，若矩形ABCD的面积是12，则平行四边形A′B′C′D′的面积是___．
15.在平面直角坐标系中，矩形ABCD的边BC在x轴上，O为线段BC的中点，矩形ABCD的顶点D(2,3)，连接AC，按照下列方法作图：
(1)以点C为圆心，适当的长度为半径画弧分别交CA、CD于点E、F；
(2)分别以点E，F为圆心，大于12EF的长为半径画弧交于点G；
(3)作射线CG交AD于H，则线段DH的长为______．
16.如图，正方形ABCD的边长为2，M是BC的中点，N是AM上的动点，过点N作EF⊥AM分别交AB，CD于点E，F.则EM+AF的最小值为_________．
三、计算题：本大题共2小题，共12分。
17.计算：a−1a+a−1a．
18.解方程：2x+xx+1=1．
四、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
先化简，再求值：a2−1a2−2a+1−11−a÷1a2−a，其中a 满足a2+2a−8=0．
20.(本小题8分)
关于x的方程x−1x−3=2+kx−3的解为非负数，则k的取值范围
21.(本小题8分)
如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连接CE．
(1)求证：BD=EC；
(2)若∠E=50°，求∠BAO的大小．
22.(本小题8分)
在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，八(1)班学生在数学实验室分组做摸球试验；每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
(1)按表格数据格式，表中的a= ．
(2)请估计：当次数s很大时，摸到白球的频率将会接近 (精确到0.1)；
(3)请推算：摸到红球的概率约是 (精确到0.1)；
(4)试估算：这一个不透明的口袋中红球有 只．
23.(本小题8分)
草长莺飞二月天，某校近期打算组织八年级600名学生进行春游活动，为了提前了解学生最想去的地点，随机抽取部分学生进行调查，其中，可选地点共有四个：A地：华昌龙之谷、B地：珍珠泉、C地：红山动物园、D地：南京国防园(每位同学只选一个地点)，根据调查结果制作了如下统计图

由图中给出的信息解答下列问题：
(1)所抽取的样本容量为______；
(2)请补全条形统计图；
(3)扇形统计图中，喜欢去D处的所对应的扇形圆心角的度数为_______；
(4)请你根据抽样调查的结果，估计该校八年级最喜欢去红山动物园的学生有多少人？
24.(本小题8分)
某汽车网站对两款价格相同，续航里程相同的汽车做了一次评测，一款为燃油车，另一款为纯电新能源车．得到相关数据如下：
(1)设两款车的续航里程均为a千米，请用含a的代数式表示燃油车和纯电新能源车的每千米行驶费用；
(2)若燃油车每千米行驶费用比纯电新能源车多0.55元．
①请分别求出这两款车的每千米行驶费用；
②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元．问：每年行驶里程超过多少千米时，新能源车的年费用更低？(年费用=年行驶费用+年其它费用)
25.(本小题8分)
如图，在平行四边形ABCD中，∠BAC=90∘，∠B=60∘，AB=6.动点P从点A出发沿AD以1cm/s速度向终点D运动，同时点Q从点C出发，以4cm/s速度沿射线CB运动，当点P到达终点时，点Q也随之停止运动，设点P运动的时间为t秒．
(1)用含t的代数式表示BQ=_；
(2)当PQ⊥BC时，求t的值；
(3)请问是否存在t的值，使得A，B，P，Q为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由．
26.(本小题8分)
如图，正方形ABCD中，在边CD的右侧作等腰三角形DCE，使DE=DC，记∠CDE为α0∘<α<90∘，连接AE，过点D作DG⊥AE，垂足为G，交EC的延长线于点F，连接AF，作EH⊥CD于H．
(1)①求∠DEA的大小(用α的代数式表示)；
②判断▵AEF的形状，并说明理由．
(2)当AB= 10，CF= 2时，求CH的长．
27.(本小题8分)
在学习了“中心对称图形…平行四边形”这一章后，同学小明对特殊四边形的探究产生了浓厚的兴趣，他发现除了已经学过的特殊四边形外，还有很多比较特殊的四边形，勇于创新的他大胆地作出这样的定义：有一个内角是直角，且对角线互相垂直的四边形称为“双直四边形”。请你根据以上定义，回答下列问题：

(1)下列关于“双直四边形”的说法，正确的有_(把所有正确的序号都填上)；
①双直四边形”的对角线不可能相等：②“双直四边形”的面积等于对角线乘积的一半；③若一个“双直四边形”是中心对称图形，则其一定是正方形
(2)如图①，正方形ABCD中，点E、F分别在边AB、AD上，连接CE,BF
，EF,CF，若AE=DF，证明：四边形BCFE为“双直四边形”；
(3)如图②，在平面直角坐标系中，已知点A(0,6)，C(8,0)，点B在线段OC
上且AB=BC，是否存在点D在第一象限，使得四边形ABCD
为“双直四边形”，若存在；求出所有点D的坐标，若不存在，请说明理由．
答案和解析
1.【答案】A
【解析】【分析】本题主要考查了轴对称图形和中心对称图形的定义，解题的关键是掌握轴对称图形：一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形；中心对称图形：在平面内，把一个图形绕着某个点旋转180∘，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．据此即可解答．
【详解】解：A、原图既是中心对称图形，又是轴对称图形，故此选项符合题意；
B、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
C、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
D、原图既不是中心对称图形，也不是轴对称图形，故此选项不合题意；
故选：A．
2.【答案】C
【解析】【分析】本题考查了抽样调查、个体、样本、样本容量；
个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目，据此结合抽样调查的定义判断即可．
【详解】解：A.该调查方式是抽样调查，原说法错误；
B.每一名考生的体育成绩是个体，原说法错误；
C.抽取的2000名考生的体育成绩是总体的一个样本，说法正确；
D.样本容量是2000，原说法错误；
故选：C．
3.【答案】A
【解析】【分析】同分母分式相加，分母不变，分子相加，进行计算即可．
【详解】解：3aa+1+3a+1=3a+3a+1=3a+1a+1=3；
故选A．
本题考查分式的加减．熟练掌握同分母分式相加，分母不变，分子相加，是解题的关键．注意结果要化为最简分式或整式．
4.【答案】C
【解析】【详解】解：平行四边形的两条对角线的一半，和平行四边形的一边能够构成三角形，
∴x2、y2、6能组成三角形，令x>y
∴x−y<620−18<6<20+18
故选C．
本题考查平行四边形的性质，熟练掌握平行四边形的性质是解题的关键．
5.【答案】D
【解析】【分析】根据分式的基本性质进行判断解答即可．
【详解】解：∵a≠b，
∴A．a+1b+1≠ab，此选项错误，不符合题意；
B.a−1b−1≠ab，此选项错误，不符合题意；
C.a2b2≠ab，此选项错误，不符合题意；
D.2a2b=ab，此选项正确，符合题意．
故选：D．
本题考查分式的基本性质，熟知分式的基本性质：分式的分子和分母同时乘或除以同一个不为零的数或式子，分式的值不变，注意不是同时加或减去一个不为零的数．
6.【答案】C
【解析】【分析】根据三角形中位线可进行求解．
【详解】解：连接BC，如图所示：
∵点D、E分别是AB，AC的中点，
∴DE=12BC，
∴要测量B、C两地的距离，只需测量DE的长；
故选C．
本题主要考查三角形中位线，熟练掌握三角形的中位线是解题的关键．
7.【答案】B
【解析】【分析】本题主要考查了从实际问题中抽象出分式方程，设规定时间为x天，则慢马的速度为800x+1里/天，快马的速度为800x−2里/天，再根据快马的速度是慢马的52倍，列出方程即可．
【详解】解：设规定时间为x天，
由题意得，800x−2=52×800x+1，
故选B．
8.【答案】C
【解析】【分析】根据函数图象中的数据可以分别求得矩形的边长BC，AB的长，从而可以求得矩形的面积．
【详解】解：如图所示，过点B、D分别作y=2x+1的平行线，交AD、BC于点E、F．
由图象和题意可得：AE=8−6=2，CF=18−16=2，BE=DF=2 5，BF=DE=16−8=8，
则AB= BE2−AE2= 20−4=4，BC=BF+CF=8+2=10，
∴矩形ABCD的面积为AB⋅BC=10×4=40．
故选：C．
本题考查动点问题的函数图象，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
9.【答案】随机
【解析】【分析】本题考查了事件的分类，发生的概率为100%即为必然事件，发生的概率为0%即为不可能事件，发生的概率为0∼100%即为随机事件，据此即可作答．
【详解】解：依题意，“任意画一个三角形，它是等腰三角形”是随机事件，
故答案为：随机
10.【答案】−12
【解析】【分析】本题考查了分式的求值，根据条件设a=k，b=3kk≠0是解题的关键．
根据ab=13，设a=k，b=3kk≠0，代入分式中化简即可得出答案．
【详解】∵ab=13
∴设a=k，b=3kk≠0
∴aa−b=kk−3k=k−2k=−12
故答案为：−12．
11.【答案】9
【解析】【分析】本题考查了频数与频率的知识．
利用频数=频率×样本容量直接计算即可．
【详解】解：∵样本容量是60，分组后，第2组的频率是0.15，
∴第2组的频数是60×0.15=9，
故答案为：9．
12.【答案】−1
【解析】【分析】根据分式的值为0的条件：分子为0且分母不为0解答即可．
【详解】解：由题意，得x−1=0x−1≠0,
解得x=−1，
故答案为：−1．
本题考查了分式的值为0的条件，熟练掌握分式的值为0的条件是解题的关键．
13.【答案】11
【解析】【分析】本题考查分式的运算，根据完全平方公式的变形运用，即可求得值．
【详解】解：x2+1x2=(x−1x)2+2=32+2=11，
故答案为：11．
14.【答案】6
【解析】【分析】根据题意可得，平行四边形A′B′C′D′的底边A′D′与矩形的长AD相等，平行四边形A′B′C′D′的高变为矩形的宽的一半，则平行四边形A′B′C′D′的面积是矩形ABCD的面积的一半，即可求解．
【详解】解：过点B′作B′E⊥A′D′于点E，
∵∠A′=30∘，
∴B′E=12A′B′=12AB，
∵A′D′=AD，S矩形ABCD=12
∴S四边形A′B′C′D′=12S矩形ABCD=12×12=6．
故答案为：6．
本题主要考查了含30∘角的直角三角形，30∘所对的直角边是斜边的一半，解题的关键是掌握矩形和平行四边形的面积公式．
15.【答案】32/1.5
【解析】【分析】如图，过点H作HM⊥AC于点M，由作法可知，CH为∠ACD的平分线，DH=MH，AB=CD=3，AD=BC=4，由勾股定理得，AC= AD2+CD2=5，由S▵ACD=S▵ACH+S▵CDH，可得12AD⋅CD=12AC⋅MH+12CD⋅DH，即12×4×3=12×5×DH+12×3×DH，计算求解即可．
解：如图，过点H作HM⊥AC于点M，
由作法可知，CH为∠ACD的平分线，
∵四边形ABCD为矩形，
∴∠D=90∘,AD=BC，
∴DH=MH，
∵D(2,3)，
∴AB=CD=3，AD=BC=4，
由勾股定理得，AC= AD2+CD2=5，
∵S▵ACD=S▵ACH+S▵CDH，
∴12AD⋅CD=12AC⋅MH+12CD⋅DH，即12×4×3=12×5×DH+12×3×DH，
解得DH=32，
故答案为：32．
本题考查作角平分线，角平分线的性质，矩形的性质，勾股定理．熟练掌握角平分线的性质与作图方法、矩形的性质是解答本题的关键．
16.【答案】 10
【解析】【分析】根据正方形的性质求得AB与BM，再由勾股定理求得AM；过F作FG⊥AB于G，证明▵ABM≌▵FGE得AM=EF，再将EF沿EM方向平移至MH，连接FH，当A、F、H三点共线时，EM+AF=FH+AF=AH的值最小，由勾股定理求出此时的AH的值便可．
【详解】解：过F作FG⊥AB于G，则FG=BC=AB，∠ABM=∠FGE=90∘，
∵正方形ABCD的边长为2，
∴AB=BC=2，∠ABC=90∘，
∵M是BC的中点，
∴BM=12BC=1，
∴AM= AB2+BM2= 5，
∵EF⊥AM，
∴∠BAM+∠AEN=∠AEN+∠GFE=90∘，
∴∠BAM=∠GFE，
∴▵ABM≌▵FGESAS，
∴AM=EF，
将EF沿EM方向平移至MH，连接FH，则EF=MH，∠AMH=90∘，EM=FH，
当A、F、H三点共线时，EM+AF=FH+AF=AH的值最小，
此时EM+AF=AH= AM2+MH2= 5+5= 10，
∴EM+AF的最小值为 10，
故答案为： 10．
本题主要考查了正方形的性质，全等三角形的性质与判定，勾股定理，平移的性质，两点之间线段最短性质，关键是通过平移变换确定EM+AF取最小值的位置．
17.【答案】解：a−1a+a−1a
=a−1a+a2−1a
=a2+a−2a．

【解析】【分析】本题考查了异分母分式加减法，先通分括号内，再进行分式的加法运算，即可作答．
18.【答案】解：去分母得：2(x+1)+x2=x(x+1)
解得：x=−2
检验：当x=−2时，x(x+1)≠0，所以x=−2是原方程的解
即原方程的解为x=−2

【解析】【分析】将分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
19.【答案】解：a2−1a2−2a+1−11−a÷1a2−a
=a2−1a−12+1a−1÷1aa−1
=a2−1+a−1a−12÷1aa−1
=a−1a+2a−12⋅aa−1
=aa+2
=a2+2a
∵a2+2a−8=0
∴a2+2a=8
∴原式=a2+2a=8．

【解析】【分析】本题考查了分式的化简求值，准确熟练地计算是解题的关键．
先利用异分母分式加减法法则计算括号里，再算括号外，然后把a的值代入化简后的式子进行计算，即可解答．
20.【答案】解：x−1x−3=2+kx−3，
去分母，得：x−1=2x−3+k，
起括号，得：x−1=2x−6+k，
移项，得：2x−x=−1+6−k，
合并同类项，得：x=5−k，
∵方程x−1x−3=2+kx−3的解为非负数，
∴x≥0且x−3≠0，
∴5−k≥0且5−k−3≠0，
解得：k≤5且k≠2，
即k的取值范围为k≤5且k≠2．

【解析】【分析】本题考查的是解分式方程，一元一次不等式的应用．先解分式方程，得到x=5−k，再由题意得到x≥0，且x−3≠0，即可求出k的取值范围．
21.【答案】(1)∵四边形ABCD是菱形，
∴AB=CD，AB//CD．
又∵BE=AB，
∴BE=CD，BE//CD．
∴四边形BECD是平行四边形．
∴BD=EC．
(2)∵四边形BECD是平行四边形，
∴BD//CE，
∴∠ABO=∠E=50°．
又∵四边形ABCD是菱形，
∴AC丄BD．
∴∠BAO=90°−∠ABO=40°．

【解析】【分析】(1)根据菱形的对边平行且相等可得AB=CD，AB//CD，然后证明得到BE=CD，BE//CD，从而证明四边形BECD是平行四边形，再根据平行四边形的对边相等即可得证．
(2)根据两直线平行，同位角相等求出∠ABO的度数，再根据菱形的对角线互相垂直可得AC⊥BD，然后根据直角三角形两锐角互余计算即可得解．
22.【答案】(1)解：a=300×0.41=123，b=606÷1500=0.404；
(2)解：当次数s很大时，摸到白球的频率将会接近0.40；
(3)解：摸到红球的概率是1−0.4=0.6；
(4)解：设红球有x只，根据题意得：xx+10=0.6，
解得：x=15；
经检验，x=15是所列方程的解且符合题意，
故答案为：15．

【解析】【分析】(1)根据频率=频数÷样本总数分别求得a、b的值即可；
(2)从表中的统计数据可知，摸到白球的频率稳定在0.4左右；
(3)摸到红球的概率为1−0.4=0.6；
(4)根据红球的概率公式得到相应方程求解即可；
考查利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：概率=所求情况数与总情况数之比．组成整体的几部分的概率之和为1．
23.【答案】(1)解：32÷40%=80
(2)80−32−24−8=16(人)
补全条形统计图如下：

(3)8÷80=10%
360∘×10%=36∘
(4)24÷80=30%
600×30%=180(人)
答：该校八年级最喜欢去红山动物园的学生大约有180人．

【解析】【分析】(1)由两个统计图可知“去A地”的有32人，占调查人数的40%，根据频率等于频数除以总数，即可求出；
(2)求出“去B地”的人数即可补全条形统计图；
(3)先求出“去D地”所占百分比，即可求出对应的圆心角度数；
(4)求出“去C地”人数占总人数的百分比，即可估计总体中“去C地”所占的百分比，进而求出总体“去C地”的人数．
本题考查扇形统计图，条形统计图及二者之间关系．理解两个图形之间数量关系是解决问题的关键．扇形统计图可以直观反映各部分在总体中所占的比例；而条形统计图可以直观反映各部分的数量．
24.【答案】(1)解：燃油车每千米行驶费用为48×8a=384a(元)，
纯电新能源车每千米行驶费用为90×0.6a=54a(元)，
答：燃油车每千米行驶费用为384a元，纯电新能源车每千米行驶费用为54a元；
(2)解：①由题意得：384a−54a=0.55，
解得：a=600，
经检验，a=600是分式方程的解，且符合题意，
∴384600=0.64(元)，54600=0.09(元)，
答：燃油车每千米行驶费用为0.64元，纯电新能源车每千米行驶费用为0.09元；
②设每年行驶里程为x千米时，买新能源车的年费用更低，
由题意得：0.64x+4800>0.09x+8100，
解得：x>6000，
答：当每年行驶里程大于6000千米时，买新能源车的年费用更低．

【解析】【分析】(1)根据表中的信息，可以表示出燃油车和纯电新能源车的每千米行驶费用；
(2)①根据燃油车的每千米行驶费用比新能源车多0.55元和表中的信息，列出分式方程，解方程，即可解决问题；②设每年行驶里程为x千米时，由年费用=年行驶费用+年其它费用，列出一元一次不等式，解不等式即可．
本题考查分式方程的应用、列代数式以及一元一次不等式的应用，解题的关键是：(1)正确列出代数式；(2)①找准等量关系，正确列出分式方程；②找出数量关系，正确列出一元一次不等式．
25.【答案】(1)解：∵∠BAC=90∘，∠B=60∘，AB=6
∴BC=2AB=12
点Q从点C出发，以4cm/s速度沿射线CB运动，
当Q在线段CB上时，
∴BQ=BC−CQ=12−4t0≤t≤3
∵动点P从点A出发沿AD以1cm/s速度向终点D运动，AD=BC=12，
∴t≤12，
当Q在CB的延长线上时，BQ=CQ−BC=4t−123(2)解：过点A作AH⊥BC于H，
∵四边形ABCD是平行四边形，∠BAC=90∘，∠ABC=60∘，
∴∠ACB=30∘，AD/​/BC，∠DAB=120∘，
∴BC=2AB=12，AC=6 3，
∵∠ACB=30∘，AH⊥BC，
∴AH=12AC=3 3，CH=9，
∵PQ⊥BC，AH⊥BC，
∴PQ//AH，
又∵AD//BC，
∴四边形AHQP是平行四边形，
∴AP=QH，
∴t=9−4t，
∴t=95；
(3)解：存在，
当AB为边时，
∵四边形ABQP是平行四边形，
∴AP=BQ，
∴t=12−4t，
∴t=125，
当AB为对角线时，
∵四边形APBQ是平行四边形，
∴AP=BQ，
∴t=4t−12，
∴t=4，
综上所述：t的值为125或4．

【解析】【分析】本题是四边形综合题，考查了平行四边形的性质，直角三角形的性质等知识，利用分类讨论思想解决问题是解题的关键．
(1)先算出BC=2AB=12，再结合点Q的运动方向、速度以及起点，进行分类讨论，即可作答．
(2)先证四边形AHQP是平行四边形，可得AP=QH，列出方程可求解；
(3)分两种情况讨论，由平行四边形的性质可得AP=BQ，列出方程可求解；
26.【答案】(1)①∵AD=CD=DE，
∴∠DEA=∠DAE，
在正方形ABCD中，∠ADC=90°，∠CDE=α，
∴∠ADE=90°+α，
∴∠DEA=12180∘−90∘+α=45∘−α2，
②△AEF是等腰直角三角形，理由如下
∵CD=DE，∠CDE=α，
∴∠DEC=12180∘−α，
∵∠DEA=45−α2，
∴∠GEF=∠DEC−∠DEA=12180−α−45−α2=45∘，
又∵DF⊥AE，AD=DE
∴DF垂直平分AE
∴FA=FE，
∴∠EAF=∠AEF=45°，
∴∠AFE=90°，
∴△AEF是等腰直角三角形；
(2)连接AC，
∵EH⊥CD
∴∠EHD=∠EHC=90°，
∵四边形ABCD是正方形，
∴AB=BC=CD=AD= 10，∠ABC=90°，
∴DE= 10，
在Rt△ABC中，AC= AB2+BC2=2 5，
在Rt△AFC中，∠AFC=90°，CF= 2，
∴EF=AF= AC2−CF2=3 2，
∴EC=2 2，
在Rt△EHD和Rt△EHC中，
EH2=ED2−DH2=EC2−CH2，
设CH=x，则DH= 10−x，
∴ 102− 10−x2=2 22−x2，
解得：x=25 10，
∴CH=25 10

【解析】【分析】(1)①利用正方形的性质、等腰三角形的性质及三角形内角和定理即可求解；②△AEF是等腰直角三角形，利用①的结论和三角形内角和定理求出∠GEF=45°，接着利用线段的垂直平分线的性质即可证明结论；
(2)连接AC，利用勾股定理求出AC、EF、EC，最后利用勾股定理得到在Rt△EHD和Rt△EHC中，EH2=ED2−DH2=EC2−CH2，设CH=x，由此建立方程解决问题．
本题主要考查了正方形的性质，全等三角形的性质与判定，线段的垂直平分线的性质，等腰三角形的判定与性质，综合性比较强，对于学生的要求比较高．
27.【答案】(1)∵“双直四边形”的对角线互相垂直，
∴“双直四边形”的面积等于对角线乘积的一半．
故②正确．
∵中心对称的四边形是平行四边形，对角线互相垂直且有一个角是直角的的平行四边形是正方形．
∴若一个“双直四边形”是中心对称图形，则其一定是正方形．
故③正确．
∵正方形是“双直四边形”，正方形的对角线相等．
故①不正确．
故答案为：②③
(2)
如图，设BF与CE的交点为O
∵四边形ABCD是正方形
∴AB=BC=AD,∠A=∠ABC=90∘,
又∵AE=DF,
∴BE=AF,
∴▵ABF≅▵BCE.
∴∠ABF=∠BCE.
∵∠ABF+∠FBC=∠ABC=90∘.
∴∠BCE+∠FBC=90∘.
∴∠BOC=90∘.
∴BF⊥CE
∵∠EBC=90∘
∴四边形BCFE为“双直四边形”
(3)假设存在点D在第一象限，使得四边形ABCD为“双直四边形”．
如图，设AC、BD的交点为H
∵A(0,6),C(8,0),
∴AO=6,CO=8,
∵AB=BC,
∴AB2=BC2
即AO2+OB2=(OC−0B)2,
62+OB2=(8−OB)2
解得OB=74
∴B(74,0)
∵BA=BC,BD⊥AC
∴AH=CH
∴H是AC的中点，
∴H(4,3)
设直线BD的解析式为y=kx+b,则
0=74k+b3=4k+b
解得k=43b=−73
∴直线BD的解析式为y=43x−73
设D(m,43m−73)
①当∠BCD=90∘时，则CD⊥BC
∴m=8,43m−73=253
则D(8,253)
②当∠BAD=90∘时
∵BA=BC,BD⊥AC
∴BD是AC
∴DA=DC
∵BD=BD
∴▵DAB≅▵DCB
∴∠DAB=∠DCB=90∘
此时D点坐标还是(8,253)．
③当∠ADC=90∘时
∵DA=DC
∴▵ADC是等腰直角三角形
∵AD2+DC2=AC2
∴2AD2=AC2
2m2+(43m−73−6)2=62+82
整理得m2−8m−7=0
m1=1,m2=7
当m=1时，43m−73=−1
此时D(1,−1)在第四象限，不符合题意．
当m=7时，43m−73=7
此时D(7,7)在第一象限，符合题意．
综上，D点坐标为(8,253)或(7,7)

【解析】【分析】(1)由“双直四边形”的定义依次判断即可．
(2)设BF、CE的交点为O点，先根据SAS证明▵ABF≅▵BCE ，于是得∠ABF=∠BCE，再证明∠BCE+∠FBC=90∘，即可得BF⊥CE，由此得四边形BCFE为“双直四边形”．
(3)先求出BD的解析式，再分三种情况讨论：①∠BCD=90∘，②∠BAD=90∘，③∠ADC=90∘，分别求出点D的坐标即可．
本题是一道四边形的综合题，主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，一次函数等知识，综合性较强，题目难度较大.熟练掌握以上知识以及分类讨论思想是解题的关键．
摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
燃油车
纯电新能源车
油箱容积：48升
电池容量：90千瓦时
油价：8元/升
电价：0.6元/千瓦时