数学九年级下册28.1 锐角三角函数课文配套ppt课件

这是一份数学九年级下册28.1 锐角三角函数课文配套ppt课件，共23页。PPT课件主要包含了学习目标等内容，欢迎下载使用。

1.理解并掌握锐角正弦的定义．2.在直角三角形中求锐角的正弦值．(重点)
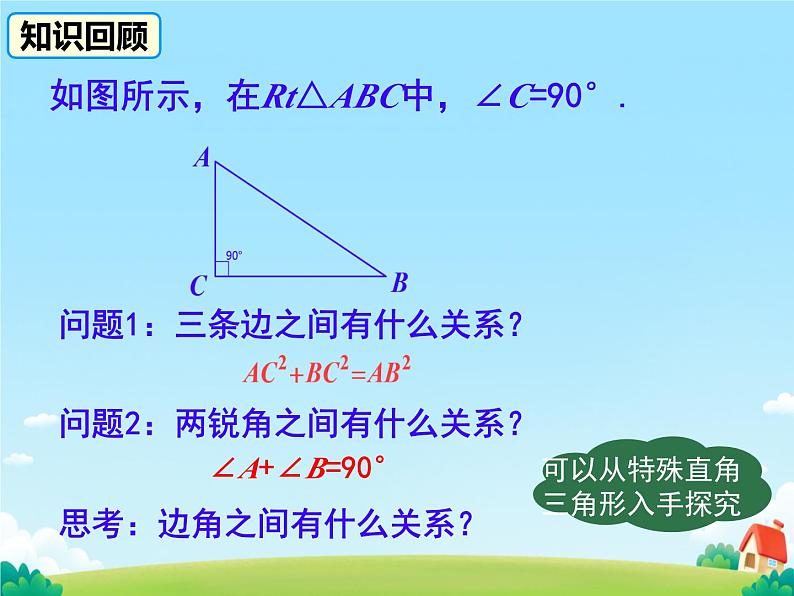
如图所示，在Rt△ABC中，∠C=90°.
问题1：三条边之间有什么关系？
问题2：两锐角之间有什么关系？
思考：边角之间有什么关系？
可以从特殊直角三角形入手探究
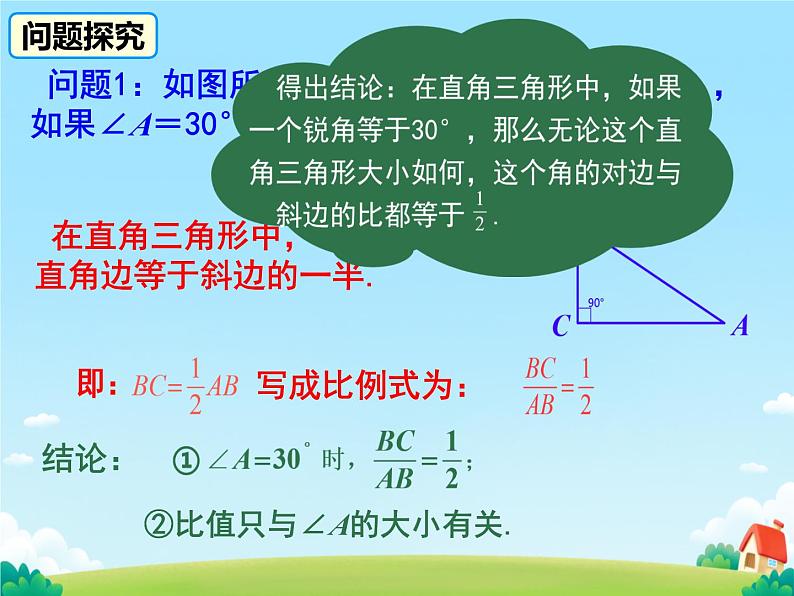
问题1：如图所示，在Rt△ABC中，∠C＝90°，如果∠A＝30°，你能说出边之间的关系吗？
在直角三角形中，30度角所对直角边等于斜边的一半.
②比值只与∠A的大小有关.
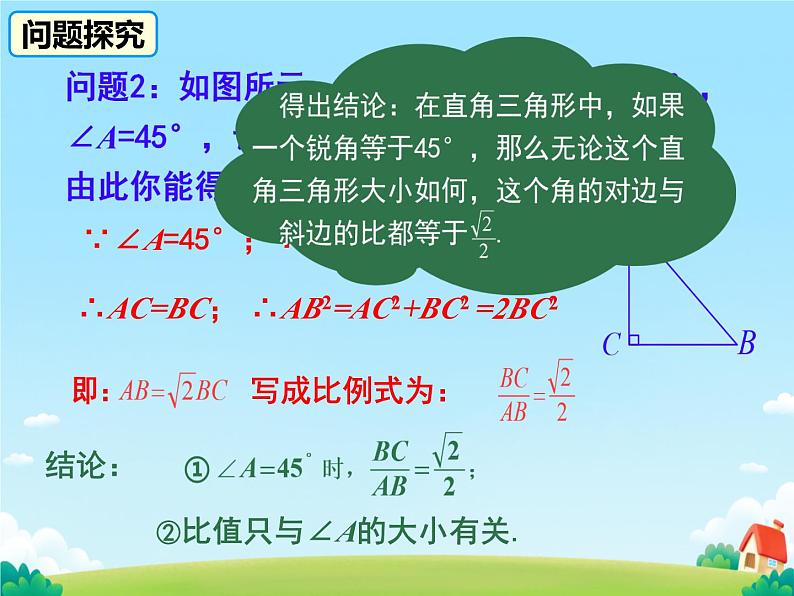
∴△ABC是等腰Rt△；
∴AB2=AC2+BC2
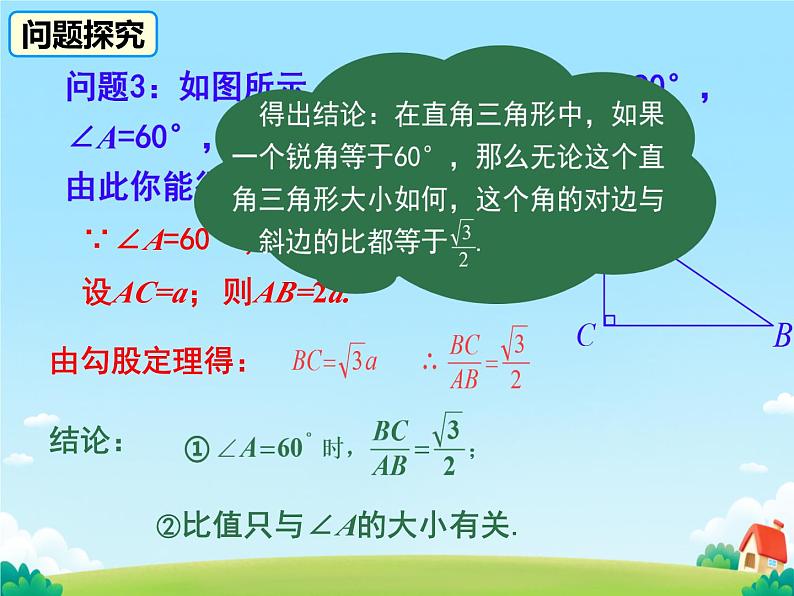
在直角三角形中，如果一个锐角等于30°，45°，60°时，那么无论这个直角三角形大小如何，这个角的对边与斜边的比都是固定值.
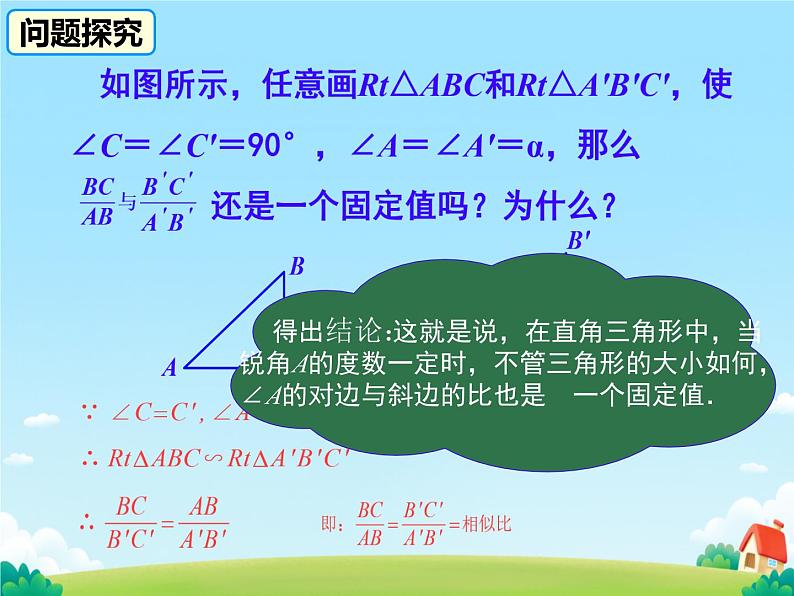
想一想：当∠A是任意一个确定的锐角时，它的对边与斜边的比是否也是一个固定值呢？
得出结论：这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比也是 一个固定值．
观察下列结论，你发现了什么？
当∠A的度数发生变化时，∠A的对边与斜边的比随∠A的变化而变化.
∠A的对边与斜边的比值
它们反应的是直角三角形的边角之间的关系.
如图，在Rt△ABC中，∠C＝90°，我们把锐角∠A的对边与斜边的比叫做∠A的正弦（sine）， 记作：sinA，
即：sinA随∠A的增大而增大.
三角函数中应注意的问题：
1.sinA,csA,tanA均是一个完整的符号，不能写成sin·A,cs·A,tan·A;
2.sinA,csA,tanA中，∠A的符号“∠”习惯上可以省略不写，但对于用三个大写字母或用阿拉伯数字表示的角，角的符号“∠”不能省略，如“sin∠ABC,sin∠1”中的“∠”的符号不能省略.
3.sin2A表示（sinA）2,cs2A表示（csA）2,tan2A表示（tanA）2.
4.在Rt△中，若∠A=∠B，则sinA=sinB；若∠A≠∠B，则sinA≠sinB，反之也成立.
例1 如图，在Rt△ABC中，∠C=90°，求sinA 和sinB的值.
解析：求sinA 和sinB的值，实质就是求∠A与∠B的对边与斜边的比.
提示：先利用勾股定理求未知的斜边与直角边的长.
已知：如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，求sin A和sin B的值.
解：如图，过点P作x轴的垂线，垂足为A .
在Rt△APO中，由勾股定理得
例2 如图，在平面直角坐标系内有一点P（3，4），连接OP，求OP与x轴正方向所夹锐角α的正弦值.
在平面直角平面坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____.
1.在Rt△ABC中，若三边长都扩大2倍，则锐角A的正弦值（ ) A.扩大2倍 B.不变 C.缩小2倍 D.无法确定
3.如图，在Rt△ABC中，∠C=90°，求sinA和sinB的值.
4.如图，在Rt△ABC中，∠C=90°，∠A=60°，求sinA的值.
5.如图，点D（0，3），O（0，0），C（4，0）在⊙A上，BD是⊙A的一条弦，则sin∠OBD=___________.
解析：连接CD，可得出∠OBD=∠OCD，根据点D（0，3），C（4，0），得OD=3，OC=4，由勾股定理得出CD=5，再在直角三角形中得出利用三角函数求出sin∠OCD即可．
7.如图，在正方形网格中有△ABC，则 sin∠ABC的值为 .
8.已知,如图，在△ABC中，CD是AB边上的高，CD=12，AD=9,BD=5,求sinA,sin∠ACD,sinB和sin∠BCD的值.