初中数学人教版九年级下册28.1 锐角三角函数优质第1课时教案

这是一份初中数学人教版九年级下册28.1 锐角三角函数优质第1课时教案，共8页。教案主要包含了教学方案，典型例题，随堂练习等内容，欢迎下载使用。


【教学方案】
28.1锐角三角函数
第1课时
第二十八章 锐角三角函数
28.1锐角三角函数
第1课时
一、 教学目标
1. 通过探究使学生知道当直角三角形的锐角固定时，它的对边与斜边的比是一个固定值，引出正弦的概念；
2.理解正弦的概念并能根据正弦的概念正确进行计算；
3.经历正弦概念的发现与学习过程，培养学生由特殊到一般的归纳推理能力；
4.引导学生体验数学活动，探索与发现新知识，使学生会用数学的思维方式去思考、发现、总结、验证.
二、 教学重难点
重点：理解锐角的正弦，并能根据正弦的定义，求直角三角形中给定锐角的正弦值.
难点：正弦的探究过程.
三、教学用具
多媒体等.

四、教学过程设计
教学
环节
教师活动
学生活动
设计意图
环节一
创设情景
【回顾】
教师活动：教师带领学生回顾直角三角形中的边的关系和角的关系，引导学生思考边角间的关系.
已知：在Rt△ABC中，∠C=90°.
三边关系：a2+b2=c2.
两锐角关系：∠A+∠B=90°.
思考：边角之间有什么关系吗？
在直角三角形中，如果有一个锐角等于30° ，那么它所对的直角边等于斜边的一半.
任意直角三角形是否也存在类似的边角关系呢？
思考并配合老师回答问题
通过直角三角形中边的关系，角的关系的复习，自然引导学生思考边角之间的关系.
环节二探究新知
【思考】
教师活动：通过含30°的直角三角形的边角关系入手，使学生更容易接受.
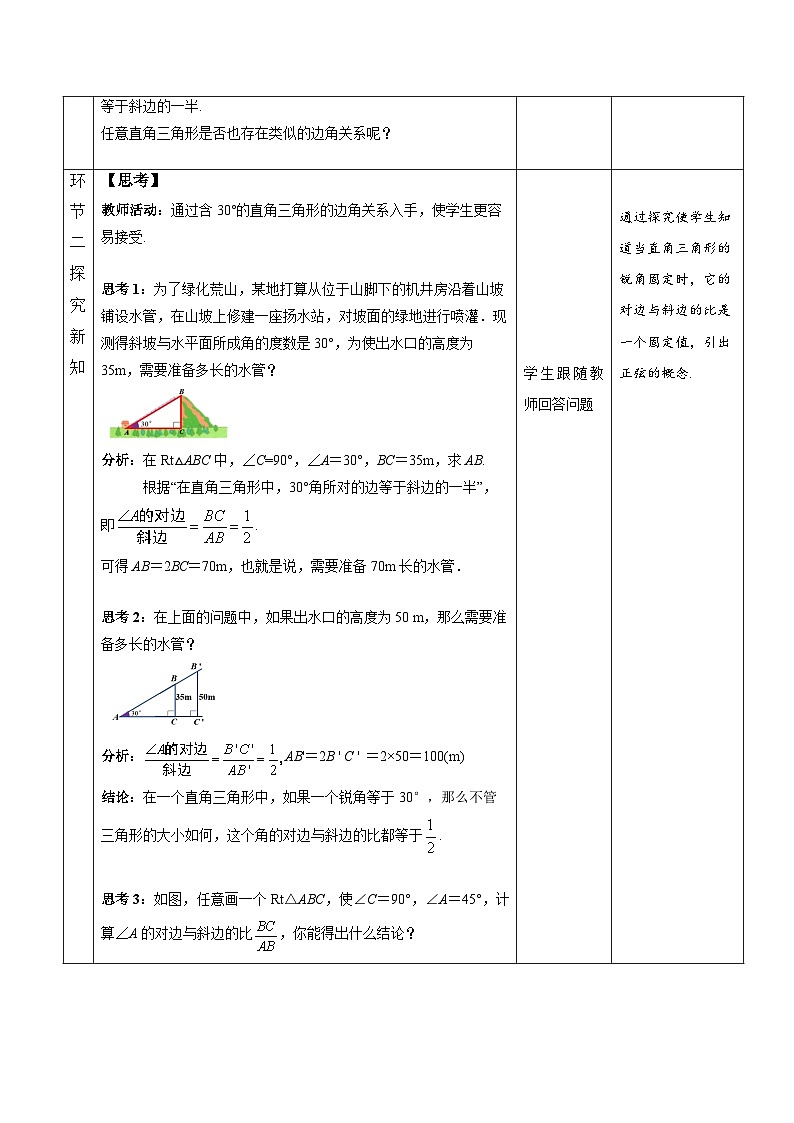
思考1：为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌．现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为35m，需要准备多长的水管？
分析：在Rt△ABC中，∠C=90°，∠A＝30°，BC＝35m，求AB.
根据“在直角三角形中，30°角所对的边等于斜边的一半”，即.
可得AB＝2BC＝70m，也就是说，需要准备70m长的水管．
思考2：在上面的问题中，如果出水口的高度为50 m，那么需要准备多长的水管？
分析：AB'＝2B ' C ' ＝2×50＝100(m)
结论：在一个直角三角形中，如果一个锐角等于30°，那么不管三角形的大小如何，这个角的对边与斜边的比都等于.
思考3：如图，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计算∠A的对边与斜边的比，你能得出什么结论？
分析：在Rt△ABC中，∠C＝90°，由于∠A＝45°，所以Rt△ABC是等腰直角三角形，由勾股定理得:
.
.
因此.
结论：在直角三角形中，当一个锐角等于45°时，不管这个直角三角形的大小如何，这个角的对边与斜边的比都等于 .
【归纳】
在Rt△ABC中，∠C=90°.
当∠A=30°时，∠A的对边与斜边的比值都等于，是一个固定值；
当∠A=45°时，∠A的对边与斜边的比值都等于，是一个固定值；
提问：一般地，当∠A 是任意一个确定的锐角时，它的对边与斜边的比是否也是一个固定值呢？
【探究】
任意画Rt△ABC和Rt△A'B'C'，使得∠C＝∠C '＝90°，∠A＝∠A'，那么与有什么关系？你能解释一下吗？
分析：由于∠C＝∠C '＝90°，∠A＝∠A'，所以Rt△ABC∽Rt△A'B'C' ，
结论：在Rt△ABC中，当锐角A的度数一定时，∠A的对边与斜边的比是一个固定值，与直角三角形的大小无关.
【归纳】
如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦（sine），记作sinA 即
例如，当∠A＝30°时，.
当∠A＝45°时，.
∠A的正弦sinA随着∠A的变化而变化.
学生跟随教师回答问题
通过探究使学生知道当直角三角形的锐角固定时，它的对边与斜边的比是一个固定值，引出正弦的概念.
环节三应用新知
【典型例题】
例1：如图，在Rt△ABC中，∠C＝90°，分别求sinA和sinB的值．
解：在Rt△ABC中，由勾股定理得
.
因此.
.
例2：如图，在Rt△ABC中，∠C＝90°，分别求sinA和sinB的值．
解：在Rt△ABC中，
.
.
因此.
【做一做】
如图，已知CD是Rt△ABC斜边上的高，则
sinA= =，
sinB==，
sin∠DCB= ，
sin∠ACD= .
答案：CD，AB，BC，AB， ，.
【归纳】
计算一个锐角的正弦值需注意：
①确定这个锐角所在的直角三角形；
②注意正弦等于这个锐角的对边与斜边的比．
集体回答
通过例题，规范学生对解题步骤的书写，让学生感受数学的严谨性.
环节四
巩固新知
【随堂练习】
教师活动：通过Pk作答的形式，让学生独立思考，再由老师带领整理思路过程.
练习1
判断对错:
①如图 (1)sinA= （ ）
(2)sinB= （ ）
(3)sinA=0.6m （ ）
(4)sinB=0.8 （ ）
②如图，sinA= （ ）
答案：√、×、×、√、×.
提醒：sinA是一个比值（注意比的顺序），无单位.
练习2
在Rt△ABC中，锐角A的对边和斜边同时扩大100倍，
sinA的值( )
A.扩大 B.缩小
C.不变 D.不能确定
答案：C .
练习3
如图，在直角△ABC中，∠C＝90，若AB＝5，
AC＝4，则sinA＝( )
A． B．
C． D．
答案：A .
练习4
在△ABC中，∠C=90°，BC=2，sinA=，
则边AC的长是( )
A． B． 5
C． D． 3
答案：A .
Pk作答
进一步巩固本节课的内容. 了解学习效果，让学生经历运用知识解决问题的过程，给学生获得成功体验的空间.
环节五
课堂小结
以思维导图的形式呈现本节课所讲解的内容.
回顾本节课所讲的内容
通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六
布置作业
巩固例题练习
教科书第64页练习1、2.
课后完成练习
通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.