2024年黑龙江省大庆市肇源县中考一模数学试题

这是一份2024年黑龙江省大庆市肇源县中考一模数学试题，共8页。试卷主要包含了4×10−5 B，定义新运算“▲”等内容，欢迎下载使用。


选择题：本题共10小题，每小题3分，共30分。
1.−2024的倒数是( ) A. 2024B. −2024C. −12024 D. 12024
2.清代诗人袁枚的一首诗《苔》中写到：“白日不到处，青春恰自来．苔花如米小，也学牡丹开”若苔花的花粉直径约为0.0000084米，数据0.0000084用科学记数法表示为( )
A. 8.4×10−5 B. 8.4×10−6 C. 8.4×10−7 D. 8.4×106
3.汉字是中华民族几千年文化的瑰宝，更是民族灵魂的纽带．以下是“南京小镇”四个字的篆体，其中能看作既是轴对称图形又是中心对称图形的是．( )
A. B. C. D.
4.若a+b=3，a−b=7，则a2−b2的值为 ( )
A. −21 B. 21 C. −10 D. 10
5.不透明的袋子中有两个小球，上面分别写着数字“1”，“2”，除数字外两个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为3的概率是( )
A. 14 B. 13 C. 12 D. 23
6.已知实数a在数轴上的对应点位置如图，则化简|a−1|− (a−2)2的结果是( )
A. 2a−3 B. −1 C. 1 D. 3−2a

7.如图，四边形ABCD为矩形，依据尺规作图的痕迹，∠α与∠β的度数之间的关系为( )
A. β=180°−α B. β=180°−12α
C. β=90°−α D. β=90°−12α
8.绿水青山就是金山银山．某工程队承接了100万平方米的荒山绿化工程，由于情况有变……，设原计划每天绿化的面积为x万平方米，列方程为100x−100(1+10%)x=20，根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了10％，结果提前20天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了10％，结果延误20天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了10％，结果延误20天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了10％，结果提前20天完成了这一任务
9.如图，在△ABC中，BC=120，高AD=60，正方形EFGH的一边在BC上，点E，F分别在AB，AC上，AD交EF于点N，则AN的长为( )
A. 15 B. 20
C. 25 D. 30
10.定义新运算“▲”: a▲b=ab(b>0),−ab(b<0).例如4▲5=45，4▲(−5)=45，则函数y=2▲x(x≠0)的图象大致是( )
A. B. C. D.
二、填空题：本题共8小题，每小题3分，共24分。
11.如果ab=23，那么aa+b= ．
12.若最简二次根式 a+1与 2能合并成一项，则a= ．
13.不等式组−x+2m的解集是x>4，那么m的取值范围是 ．
14.如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直于马路的方向走过斑马线更为合理，这一想法体现的数学依据是____________________．
一个等腰三角形的周长是10，腰长是x，底边长是y，则y关于x的函数解析式为 ．
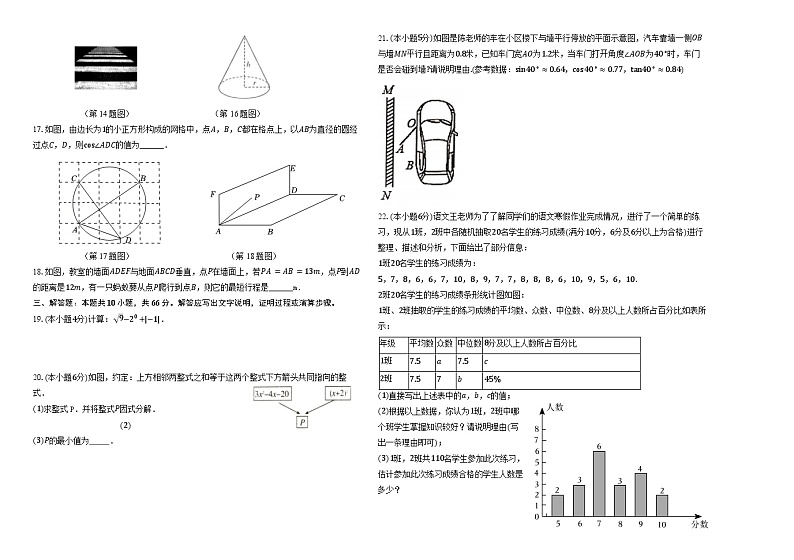
16.为了给同学庆祝生日，小明自己动手用扇形纸片制作了一顶圆锥形生日帽，生日帽的底面圆半径r为7cm，高ℎ为24cm，则该扇形纸片的面积为 cm2．

（第14题图） （第16题图）
17.如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C，D，则cs∠ADC的值为______．
（第17题图） （第18题图）
18.如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上，若PA=AB=13m，点P到AD的距离是12m，有一只蚂蚁要从点P爬行到点B，则它的最短行程是______m．
三、解答题：本题共10小题，共66分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题4分)计算： 9−20+|−1|．
20.(本小题6分)如图，约定：上方相邻两整式之和等于这两个整式下方箭头共同指向的整式．
(1)求整式P．并将整式P因式分解．
(2)
(3)P的最小值为 ．
21.(本小题5分)如图是陈老师的车在小区楼下与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，已知车门宽AO为1.2米，当车门打开角度∠AOB为40∘时，车门是否会碰到墙?请说明理由.(参考数据：sin40∘≈0.64，cs40∘≈0.77，tan40∘≈0.84)
22.(本小题6分)语文王老师为了了解同学们的语文寒假作业完成情况，进行了一个简单的练习，现从1班，2班中各随机抽取20名学生的练习成绩(满分10分，6分及6分以上为合格)进行整理、描述和分析，下面给出了部分信息：
1班20名学生的练习成绩为：
5，7，8，6，6，7，10，8，9，7，7，8，8，8，6，10，9，5，6，10．
2班20名学生的练习成绩条形统计图如图：
1班、2班抽取的学生的练习成绩的平均数、众数、中位数、8分及以上人数所占百分比如表所示：
(1)直接写出上述表中的a，b，c的值；
(2)根据以上数据，你认为1班，2班中哪个班学生掌握知识较好？请说明理由(写出一条理由即可)；
(3)1班，2班共110名学生参加此次练习，估计参加此次练习成绩合格的学生人数是多少？
23.(本小题7分)为了加强对校内外的安全监控，创建平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格、有效监控半径如表所示．经调查，购买1台甲型设备比购买1台乙型设备少150元，购买3台甲型设备比购买2台乙型设备多150元．
(1)求a，b的值．
(2)若购买该批设备的资金不超过7200元，且两种型号的设备均要至少买一台，则学校有哪几种购买方案？
(3)在(2)的条件下，若要求有效监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案．
24.(本小题7分)如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l/​/y轴，且直线l分别与反比例函数y=8x(x>0)和y=kx(x>0)的图象交于P、Q两点.S△POQ=14．
(1)求k的值；
(2)当∠QOM=45°时，求直线OQ的解析式；
(3)在(2)的条件下，若x轴上有一点N，使得△NOQ为等腰三角形，请直接写出所有满足条件的N点的坐标．
25.(本小题7分)如图，在四边形ABCD中，对角线AC，BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．
(1)求证：四边形ABCD是矩形；
(2)若∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数．
26.(本小题7分)如图①，部队、学校、仓库、基地在同一条直线上．学校开展国防教育活动，师生乘坐校车从学校出发前往基地，与此同时，教官们乘坐客车从部队出发，到仓库领取装备后再前往基地；到达基地后，他们需要10min整理装备．客车和校车离部队的 距离y(km)与所用时间t(ℎ)的函数图像如图②所示，其中，点C在线段AB上．
(1)部队和基地相距______km，客车到达仓库前的速度为______km/ℎ．
(2)求校车离部队的距离y与t的函数表达式以及教官们领取装备所用的时间．
(3)为确保师生到达基地时装备已经整理完毕，则客车第二次出发时的 速度至少是多少？
27.(本小题8分)如图，AB是⊙O的直径，点D、E在⊙O上，连接AE、ED、DA，连接BD并延长至点C，使得∠DAC=∠AED．
(1)求证：AC是⊙O的切线；
(2)若点E是BD的中点，AE与BC交于点F，
①求证：CA=CF；
②若⊙O的半径为3，BF=2，求AC的长．
28.(本小题9分)如图，抛物线y=12x2−x−4与x轴交于点A和B，与y轴交于点C．
(1)求A、B、C三点坐标；
(2)如图1，动点P从点A出发，在线段AB上以每秒1个单位长度向点B做匀速运动，同时，动点Q从点B出发，在线段BC上以每秒 2个单位长度向点C做匀速运动，当其中一点到达终点时，另一点随之停止运动，连接PQ，设运动时间为t秒，问P、Q两点运动多久后△PBQ的面积S最大，最大面积是多少？
(3)如图2，点D为抛物线上一动点，直线AD交y轴于点E，直线BD交y轴于点F，求CECF的值．
肇源县初四毕业班第一次摸底考试
数学参考答案
选择题
1. C 2. B 3. C 4. B 5. C 6. A 7. D
8. A 9. B 10. C
二、填空题
11. 25 12. 1 13. m≤4 14. 垂线段最短
15. y=10−2x 16. 175π 17. 3 1313 18. 5 26 m
三、解答题
19. 解：原式=3−1+1 ------------3分(每个运算结果答对给1分）
=3． --------------4分
20. 解：
(1)P=3x2−4x−20+(x+2)2
=3x2−4x−20+x2+4x+4------------1分
=4x2−16． -----------2分

4x 2 - 16 =4(x2−4) −−−−−−−−−−−−3分 -
=4(x+2)(x−2)． ------------4分

P=4x2−16，
∵x2≥0， -----------5分
∴当x=0时，P的最小值为−16． -----------6分

21. 解：当车门打开角度∠AOB为40°时，车门不会碰到墙.理由如下：
如图，过点A作AC⊥OB，垂足为点C．) -----------1分
在Rt△ACO中，∵∠AOC=40°，AO=1.2米，
∴AC=AO·sin∠AOC≈1.2×0.64=0.768(米)． -----------3分
∵汽车靠墙一侧OB与墙MN平行且距离为0.8米，0.768<0.8，-----------4分
∴当车门打开角度∠AOB为40°时，车门不会碰到墙． -----------5分
22. 解：(1)a=8，b=7，c=50%； -----------3分
(2)1班学生掌握知识较好，
理由如下：
因为1班和2班平均分和众数均相等，但是1班的中位数和8分及以上人数所占百分比都比2班的高，因此我认为1班学生掌握知识较好；（答案不唯一，写出一条理由即可） ----------4分
(3)110×18+1820+20=99(人)-----------5分
答：估计参加此次练习成绩合格的学生人数是99人． )-----------6分
23. （1）依题意，得b−a=150,3a−2b=150, -----------1分
解得a=450,b=600.) -----------2分
设购买甲型设备x台，则购买乙型设备(15−x)台，
依题意，得x≥1,15−x≥1,450x+600(15−x)≤7200, ----------3分
解得12≤x≤14.
∵x为整数，∴x=12，13，14． ----------4分
故学校有三种购买方案，方案1：购买甲型设备12台，乙型设备3台；方案2：购买甲型设备13台，乙型设备2台；方案3：购买甲型设备14台，乙型设备1台．----------5分
依题意，得100x+150(15−x)≥1600， 解得x≤13，
∴12≤x≤13， ∴x=12或13． ----------6分
方案1：当x=12时，所需资金为450×12+600×3=7200(元)，
方案2：当x=13时，所需资金为450×13+600×2=7050(元)．
∵7200>7050，∴方案2省钱．
即最省钱的购买方案为购买甲型设备13台，乙型设备2台．---------7分
24. 解：(1)∵S△POQ=S△POM+S△MOQ=14，S△POM=12×8=4，S△QOM=12|k|，
∴12|k|+4=14，
∵k<0，
∴k=−20； ----------2分
(2)由(1)得反比例函数的解析式为y=−20x，
∵∠QOM=45°，l/​/y轴，
∴∠QOM=∠OQM=45°，
∴MO=MQ， ---------3分
设Q(a,−a)，
∴−a2=−20，
∴a=2 5(负值已舍去)，
∴点Q的坐标为(2 5,−2 5)，
设直线OQ的解析式为y=kx，将点Q的坐标(2 5,−2 5)代入得：
−2 5=2 5k，
解得：k=−1，
∴直线OQ的解析式为y=−x；- ---------4分
(3)∴OQ= (2 5)2+(2 5)2=2 10，
若△NOQ为等腰三角形，可分三种情况：
①若OQ=ON=2 10，则N(2 10,0)或(−2 10,0)； ----------5分
②若QO=ON，则NO=2OM=4 5，则N(4 5,0)； ----------6分
③若NO=NQ，设点N(n,0)，则n2=(n−2 5)2+(2 5)2，解得：n=2 5，
∴n(2 5,0)， ----------7分
综上所述，满足条件的点N的坐标为：(2 10,0)或(−2 10,0)或(4 5,0)或(2 5,0)．
25.(1)证明：∵AO=CO，BO=DO，
∴四边形ABCD是平行四边形， ----------2分
∴∠ABC=∠ADC，
∵∠ABC+∠ADC=180°，
∴∠ABC=∠ADC=90°， ----------3分
∴四边形ABCD是矩形； ---------4分
(2)解：∵∠ADC=90°，∠ADF：∠FDC=3：2，
∴∠FDC=36°，
∵DF⊥AC，
∴∠DCO=90°−36°=54°， ----------5分
∵四边形ABCD是矩形，
∴CO=OD，
∴∠ODC=∠DCO=54°， ----------6分
∴∠BDF=∠ODC−∠FDC=18°．--------7分
26. （1）解：100，80，---------2分
（2）校车离部队的距离y与t的函数表达式为y=kt+b，
把0,20，0.5,40代入解析式得：
b=200.5k+b=40,
解得k=40b=20,
∴校车离部队的距离y与t的函数表达式为y=40t+20； ----------4分
把y=80代入y=40t+20得，80=40t+20，
解得t=1.5，
∵客车的速度为80km/ℎ，
∴客车到达仓库的时间为80÷80=1ℎ，
∵1.5−1=0.5ℎ，
∴教官们领取装备所用的时间0.5ℎ；---------5分
（3）把y=100代入y=40x+20得，100=40x+20，
解得x=2，
∴校车2小时到达营地，为确保师生到达基地时装备已经整理完毕，
客车到达基地的时间t≤2−16=116，
∴客车第二次出发时的速度v≥100−80÷116−32=60km/ℎ．
∴客车第二次出发时的速度至少是60km/ℎ．---------7分

27. (1)证明：∵AB是⊙O的直径，
∴∠ADB=90°，
∴∠DBA+∠DAB=90°，
∵∠DEA=∠DBA，∠DAC=∠DEA，
∴∠DBA=∠DAC，
∴∠DAC+∠DAB=90°，∴∠CAB=90°，
∵AB是⊙O的直径，
∴AC是⊙O的切线；---------3分
(2)①证明：∵点E是BD的中点，
∴∠BAE=∠DAE，
∵∠CFA=∠DBA+∠BAE，∠CAF=∠DAC+∠DAE，∠DBA=∠DAC，
∴∠CFA=∠CAF，
∴CA=CF；---------5分
②解：设CA=CF=x，
则BC=CF+BF=x+2，
∵⊙O的半径为3，
∴AB=6，
在Rt△ABC中，CA2+AB2=BC2，
即：x2+62=(x+2)2，
解得：x=8，
∴AC=8． ---------7分
28. 解：(1)令y=0，即有：12x2−x−4=0，
利用因式分解法，求得：x1=−2，x2=4，
结合图形，可知A(−2,0)、B(4,0)，
令x=0，则y=12x2−x−4=−4，
则有C点坐标为：C(0,−4)，
即A(−2,0)、B(4,0)，C(0,−4)；--------3分
(2)∵A(−2,0)、B(4,0)，C(0,−4)，
∴AO=2、BO=4=CO，
∴△BOC是等腰直角三角形，AB=AO+BO=2+4=6，
∴BC= OC2+BO2= 42+42=4 2，
过Q点作QN⊥AB于N点，如图，
根据运动的特点，可得：AP=t，BQ= 2t，
∴BP=6−t，
∵AB=6，BC=4 2，
∴t的取值范围为：0即0∵△BOC是等腰直角三角形，
∴∠OBC=45°，
∵QN⊥AB，
∴∠QNB=90°，
∴∠NQB=∠OBC=45°，
∴△QNB是等腰直角三角形，QN=BN，
∵BQ= 2t，BQ= BN2+NQ2，QN=BN，
∴QN=BN=t，
∴S△PBQ=12×BP×QN=12(6−t)t=−12(t−3)2+92，
∵0∴当t=3时，S△PBQ有最大值，最大值为92，
即运动时间t=3秒时，S△PBQ有最大值，最大值为92；---------6分
(3)根据题意，设点D的坐标为：D(m,12m2−m−4)，
设直线AD的解析式为：y=kx+b，
∵A(−2,0)，
∴−2k+b=0km+b=12m2−m−4，
解得b=m−4k=m−42，
即直线AD的解析式为：y=m−42x+m−4，
∴令x=0，y=m−42x+m−4=m−4，
∴E点坐标为：(0,m−4)，
∵C(0,−4)，
∴CE=|m−4+4|=|m|，
同理可求出直线BD的解析式为：y=m+22x−2(m+2)，
∴令x=0，y=m+22x−2(m+2)=−2(m+2)，
∴F点坐标为：(0,−2m−4)，
∵C(0,−4)，
∴CF=|−2m−4+4|=|2m|，
根据题意可知：若m=0，则可知E、F、D、C四点重合，
此时不符合题意，故m≠0，
∴CECF=|m||2m|=|m|2|m|=12，
即CECF的值为12． ---------9分
班级
姓名
考号
题号
一
二
三
总分
得分
年级
平均数
众数
中位数
8分及以上人数所占百分比
1班
7.5
a
7.5
c
2班
7.5
7
b
45%
班级
姓名
考号
甲型
乙型
价格/(元/台)
a
b
有效监控半径/(米/台)
100
150