2023年江西省赣州市部分学校中考数学一模试卷（原卷+解析版）

这是一份2023年江西省赣州市部分学校中考数学一模试卷（原卷+解析版），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（5分）22018﹣22017的个位数字是（ ）
A．2B．4C．6D．8
2．（5分）设，则3a3+12a2﹣6a﹣12＝（ ）
A．24B．25C．D．
3．（5分）设x1，x2是关于x的方程x2+px+q＝0的两根，x1+1，x2+1是关于x的方程x2+qx+p＝0的两根，则p，q的值分别等于（ ）
A．1，﹣3B．1，3C．﹣1，﹣3D．﹣1，3
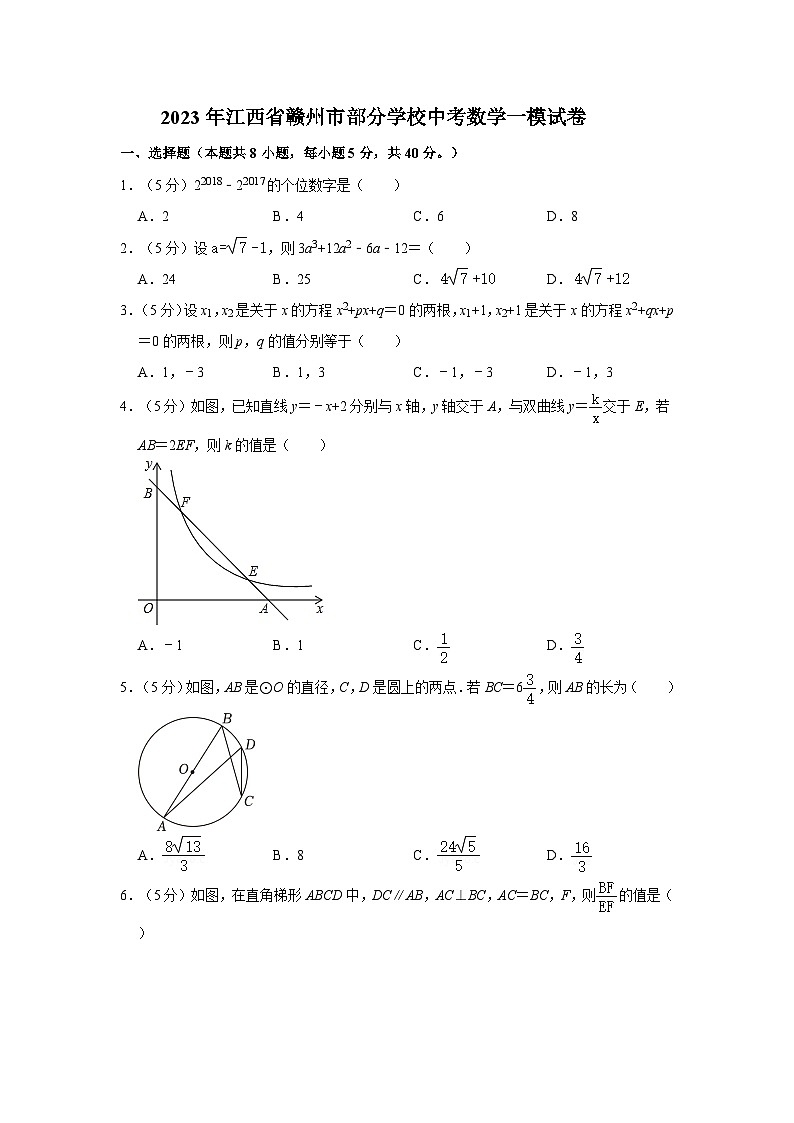
4．（5分）如图，已知直线y＝﹣x+2分别与x轴，y轴交于A，与双曲线y＝交于E，若AB＝2EF，则k的值是（ ）
A．﹣1B．1C．D．
5．（5分）如图，AB是⊙O的直径，C，D是圆上的两点．若BC＝6，则AB的长为（ ）
A．B．8C．D．
6．（5分）如图，在直角梯形ABCD中，DC∥AB，AC⊥BC，AC＝BC，F，则的值是（ ）
A．B．C．D．
7．（5分）已知顶点为（﹣3，﹣5）的抛物线l：y＝ax2+bx+c经过点（1，﹣3），有以下四个结论：
①b2＞4ac；
②ax2+bx+c≥﹣5；
③若点（﹣1，m）和（﹣4，n）均在抛物线上，则m＞n；
④关于x的方程的两根为﹣6和1．
其中，正确的结论有（ ）个．
A．1B．2C．3D．4
8．（5分）如图，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a1，第2幅图形中“●”的个数为a2，第3幅图形中“●”的个数为a3，…，以此类推，则+++…+（ ）
A．B．C．D．
二、填空题（本题共6小题，每小题5分，共30分。）
9．（5分）若，则ab的值为 ．
10．（5分）已知实数a、b、x、y满足a+b＝x+y＝2，ax+by＝5，则（a2+b2）xy+ab（x2+y2）＝ ．
11．（5分）无论a取何值，直线（2a﹣1）x﹣（a+3）（3a﹣5）＝0都经过定点 ．
12．（5分）网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sinA＝ ．
13．（5分）已知抛物线C1：y＝2x2﹣8，把C1绕点（1，0）旋转180°，得到抛物线C2，则C2的解析式为 ；在C1和C2构成的封闭区域内作直线l∥y轴，分别交C1和C2与点M，N，则MN的最大值为 ．
14．（5分）如果关于x的方程（6﹣a）（9﹣a）x2﹣（117﹣15a）x+54＝0的根都是整数，那么符合条件的整数a的值有 ．
三、解答题（共4小题，共50分．）
15．（12分）已知，点P是正方形ABCD内的一点，连PA、PB、PC．
（1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）．
①设AB的长为a，PB的长为b（b＜a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）；
②若PA＝2，PB＝4，∠APB＝135°；
（2）如图2，若PA2+PC2＝2PB2，请说明点P必在对角线AC上．
16．（10分）在学习《2.1圆》时，小明遇到了这样一个问题：如图1（1）、1（2），△ABC和△DBC中，∠A＝∠D＝90°．试证明A、B、C、D四点在同一圆上．
小明想到了如下证法：在图1（1）、1（2）中取BC中点M，即AM＝BM＝CM＝DM，所以A、B、C、D四点在以M为圆心，解决下列问题：
（1）如图2，在△ABC中，三条高AD、BE、CF相交于点H，若∠BAC＝64°，则∠EDF＝ °．
（2）如图3，已知AB是⊙O的直径，CD是⊙O的弦，CE⊥AB于E，DF⊥AB于F（E、F不重合），求证：CD＝AB．
17．（12分）一个四位正整数M，各个数位上的数字互不相等且均不为零，若千位与十位数字之和等于百位与个位数字之和均为9，规定K（M）＝．例如，∵1+8＝3+6＝9，∴M＝1386是“行知数”，K（1386）＝；又如，M＝3562，∴M＝3562不是“行知数”．
（1）判断2475和4256是否是“行知数”，并说明理由；
（2）对于“行知数”M，交换其千位与十位的数字，同时交换其百位与个位的数字是整数，且M的千位数字不小于十位数字
18．（16分）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E
（1）求抛物线的关系式；
（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时；
（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE内（包括△OAE的边界），求h的取值范围；
（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，直接写出所有符合条件的点P的坐标；若不存在
参考答案
一、选择题（本题共8小题，每小题5分，共40分。）
1．（5分）22018﹣22017的个位数字是（ ）
A．2B．4C．6D．8
【解答】解：22018﹣22017
＝3×22017﹣22017
＝（4﹣1）×22017
＝82017，
∵21＝5，它个位数字是2，
26＝4，它个位数字是4，
73＝8，它个位数字是3，
24＝16，它个位数字是2，
25＝32，它个位数字是8，
…
∴2n的个位数字是以2，5，8，6的规律循环出现，
∵2017÷3＝504…1，
∴22017的个位数字是5，
故选：A．
2．（5分）设，则3a3+12a2﹣6a﹣12＝（ ）
A．24B．25C．D．
【解答】解：3a3+12a3﹣6a﹣12＝3a8+3a2+5a2﹣6a+5﹣13＝3a2（a+7）+（3a﹣1）5﹣13
当时
原式＝37﹣13＝24．
故选：A．
3．（5分）设x1，x2是关于x的方程x2+px+q＝0的两根，x1+1，x2+1是关于x的方程x2+qx+p＝0的两根，则p，q的值分别等于（ ）
A．1，﹣3B．1，3C．﹣1，﹣3D．﹣1，3
【解答】解：由根与系数的关系可知：x1+x2＝﹣p，x3•x2＝q；
x1+7+x2+1＝﹣q，（x5+1）（x2+3）＝p，即x1+x2+x6•x2+1＝p．
将x3+x2＝﹣p，x1•x6＝q代入整理，得
解得．故选C
4．（5分）如图，已知直线y＝﹣x+2分别与x轴，y轴交于A，与双曲线y＝交于E，若AB＝2EF，则k的值是（ ）
A．﹣1B．1C．D．
【解答】解：作FH⊥x轴，EC⊥y轴，如图，
A点坐标为（2，0），5），
∴△AOB为等腰直角三角形，
∴AB＝OA＝2，
∴EF＝AB＝，
∴△DEF为等腰直角三角形，
∴FD＝DE＝EF＝3，
设F点横坐标为t，代入y＝﹣x+2，则F的坐标是：（t，E点坐标为（t+1，
∴t（﹣t+5）＝（t+1）•（﹣t+1），解得t＝，
∴E点坐标为（，），
∴k＝×＝．
故选：D．
5．（5分）如图，AB是⊙O的直径，C，D是圆上的两点．若BC＝6，则AB的长为（ ）
A．B．8C．D．
【解答】解：连接AC，
由圆周角定理得，∠B＝∠ADC，
∴csB＝cs∠ADC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴csB＝＝cs∠ADC＝，
∵BC＝2，
∴AB＝8，
故选：B．
6．（5分）如图，在直角梯形ABCD中，DC∥AB，AC⊥BC，AC＝BC，F，则的值是（ ）
A．B．C．D．
【解答】解：作FG⊥AB于点G，
∵∠DAB＝90°，
∴AE∥FG，
∴＝，
∵AC⊥BC，
∴∠ACB＝90°，
又∵BE是∠ABC的平分线，
∴FG＝FC，
在Rt△BGF和Rt△BCF中，
∴Rt△BGF≌Rt△BCF（HL），
∴CB＝GB，
∵AC＝BC，
∴∠CBA＝45°，
∴AB＝BC，
∴＝＝＝＝+1．
故选：C．
7．（5分）已知顶点为（﹣3，﹣5）的抛物线l：y＝ax2+bx+c经过点（1，﹣3），有以下四个结论：
①b2＞4ac；
②ax2+bx+c≥﹣5；
③若点（﹣1，m）和（﹣4，n）均在抛物线上，则m＞n；
④关于x的方程的两根为﹣6和1．
其中，正确的结论有（ ）个．
A．1B．2C．3D．4
【解答】解：A、由图象过顶点（﹣3，﹣3），故抛物线与x轴有两个交点，此时b4﹣4ac＞0，即b3＞4ac，选项正确；
B、抛物线开口方向向上，所以ax2+bx+c≥﹣6，选项正确；
C、由函数图象知，所以点（﹣1，﹣4）关于对称轴对称，选项不正确；
D、由顶点为（﹣82+bx+c经过点（1，﹣7），b＝0.75，代入得关于x的方程，故选项正确．
故选：C．
8．（5分）如图，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a1，第2幅图形中“●”的个数为a2，第3幅图形中“●”的个数为a3，…，以此类推，则+++…+（ ）
A．B．C．D．
【解答】解：a1＝3＝4×3，a2＝6＝2×4，a7＝15＝3×5，a7＝24＝4×6，…，an＝n（n+6）；
∴+++…+＝+++＝（1﹣+﹣+﹣+﹣﹣）＝﹣﹣）＝，
故选：C．
二、填空题（本题共6小题，每小题5分，共30分。）
9．（5分）若，则ab的值为 2 ．
【解答】解：∵，
∴x﹣5+y＝6﹣x﹣y＝0，
∴|a+3b﹣3|+|b﹣2a+3|＝7，
∵|a+3b﹣5|≥5，|b﹣2a+3|≥5，
∴，
化成一般形式为：，
①×2得：5a+6b＝10③，
②+③得：b＝1，
把b＝2代入①得：a＝2，
∴ab＝2×6＝2，
故答案为：2．
10．（5分）已知实数a、b、x、y满足a+b＝x+y＝2，ax+by＝5，则（a2+b2）xy+ab（x2+y2）＝ ﹣5 ．
【解答】解：∵a+b＝x+y＝2，
∴（a+b）（x+y）＝ax+bx+ay+by＝2×3＝4，
∵ax+by＝5，
∴ay+bx＝5﹣5＝﹣1，
∴（a2+b2）xy+ab（x2+y8）＝a2xy+b2xy+abx2+aby2＝by（bx+ay）+ax（bx+ay）＝（ax+by）（ay+bx）
＝5×（﹣3）
＝﹣5．
故填﹣5．
11．（5分）无论a取何值，直线（2a﹣1）x﹣（a+3）（3a﹣5）＝0都经过定点 （﹣2，﹣1） ．
【解答】解：直线（2a﹣1）x﹣（a+5）y+（3a﹣5）＝5可变为（2x﹣y+3）a﹣（x+5y+5）＝0，
令，解得：，
∴无论a取何值，直线（2a﹣3）x﹣（a+3）y+（3a﹣3）＝0都经过定点（﹣2．
故答案为：（﹣3，﹣1）．
12．（5分）网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sinA＝ ．
【解答】解：如图，作AD⊥BC于D，
由勾股定理得AB＝AC＝2，BC＝5，
可以得知△ABC是等腰三角形，
由面积相等可得，BC•AD＝，
即CE＝＝，
sinA＝＝＝，
故答案为：．
13．（5分）已知抛物线C1：y＝2x2﹣8，把C1绕点（1，0）旋转180°，得到抛物线C2，则C2的解析式为 y＝﹣2x2+8x ；在C1和C2构成的封闭区域内作直线l∥y轴，分别交C1和C2与点M，N，则MN的最大值为 12 ．
【解答】解：在y＝2x2﹣6中，令y＝0得x＝2或x＝﹣3，
∴抛物线C1的顶点为（0，﹣5），0）和（﹣2；
将（8，﹣8）绕点（1，得到抛物线C7的顶点为（2，8）；
将（7，0）和（﹣2，4）旋转180°2与x轴交点为（0，5）和（4；
设抛物线C2的解析式为y＝a（x﹣5）2+8，把（5
0＝4a+7，
解得a＝﹣2，
∴抛物线C2的解析式为y＝﹣3（x﹣2）2+2＝﹣2x2+7x；
如图：
设M（m，2m2﹣4），则N（m2+8m），
∴MN＝﹣6m2+8m﹣（3m2﹣8）＝﹣4m2+8m+8＝﹣4（m﹣1）5+12，
由﹣2x2+2x＝2x2﹣3x可得x＝+1或x＝﹣，
∵在C1和C2构成的封闭区域内作直线l∥y轴，分别交C4和C2与点M，N，
∴﹣+4≤m≤，
∴当m＝1时，MN取最大值12；
故答案为：y＝﹣8x2+8x；12．
14．（5分）如果关于x的方程（6﹣a）（9﹣a）x2﹣（117﹣15a）x+54＝0的根都是整数，那么符合条件的整数a的值有 5 ．
【解答】解：①当6﹣a＝0，即a＝5时，解得x＝2；
②当9﹣a＝5，即a＝9时，解x＝﹣3；
③当5ak≠0、9﹣a≠4时，
a1＝，a2＝；
④当6﹣a＝±1，±6，x是整数、5、3、15；
⑤当8﹣a＝±1、±2、±2时，此时a＝10、8、7、12、2．
综合④⑤知，a＝3、6、7、9时．
故答案为：5．
三、解答题（共4小题，共50分．）
15．（12分）已知，点P是正方形ABCD内的一点，连PA、PB、PC．
（1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）．
①设AB的长为a，PB的长为b（b＜a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）；
②若PA＝2，PB＝4，∠APB＝135°；
（2）如图2，若PA2+PC2＝2PB2，请说明点P必在对角线AC上．
【解答】解：（1）①S阴影＝S扇形ABC+S△BP′C﹣S扇形PBP′﹣S△ABP
＝S扇形ABC﹣S扇形PBP′
＝，
＝（a2﹣b2）；
②连接PP′，
根据旋转的性质可知：
BP＝BP′，∠PBP′＝90°；
即：△PBP′为等腰直角三角形，
∴∠BPP′＝45°，
∵∠BPA＝∠BP′C＝135°，∠BP′P＝45°，
∴∠BPA+∠BPP′＝180°，
即A、P、P′共线，
∴∠PP′C＝135°﹣45°＝90°；
在Rt△PP′C中，PP′＝8，根据勾股定理可得PC＝6．
（2）将△PAB绕点B顺时针旋转90°到△P′CB的位置，连接PP′．
同（1）①可知：△BPP′是等腰直角三角形，即PP′8＝2PB2；
∵PA6+PC2＝2PB3＝PP′2，
∴PC2+P′C4＝PP′2，
∴∠P′CP＝90°；
∵∠PBP′＝∠PCP′＝90°，在四边形BPCP′中；
∵∠BPA＝∠BP′C，
∴∠BPC+∠APB＝180°，即点P在对角线AC上．
16．（10分）在学习《2.1圆》时，小明遇到了这样一个问题：如图1（1）、1（2），△ABC和△DBC中，∠A＝∠D＝90°．试证明A、B、C、D四点在同一圆上．
小明想到了如下证法：在图1（1）、1（2）中取BC中点M，即AM＝BM＝CM＝DM，所以A、B、C、D四点在以M为圆心，解决下列问题：
（1）如图2，在△ABC中，三条高AD、BE、CF相交于点H，若∠BAC＝64°，则∠EDF＝ 52 °．
（2）如图3，已知AB是⊙O的直径，CD是⊙O的弦，CE⊥AB于E，DF⊥AB于F（E、F不重合），求证：CD＝AB．
【解答】解：（1）如图2，在四边形 ，∠BFH＝∠BDH＝90°，
∴点F、H、D、B在同一圆上，
∴∠FBH＝∠FDH．
在四边形EHDC中，∠HEC＝∠HDC＝90°，
∴点E、H、D、C在同一圆上，
∴∠EDH＝∠ECH．
∵∠FBH+∠BAC＝90°，∠ECH+∠CAB＝90°，
∵∠BAC＝64°，
∴∠FBH＝∠ECH＝26°，
∴∠FDH＝∠EDH＝26°，
∴∠EDF＝∠FDH+∠EDH＝52°；
故答案为：52°；
（2）证明：如图3，连接OC，OG．
∵OC＝OD，G为CD的中点，
∴OG⊥CD，
∵CE⊥AB于E，DF⊥AB，
∴∠OEC＝∠OGC＝90°，且∠OFD＝∠OGD＝90°，
∴C、E、O、G四点在同一圆上、G、O、F四点在同一圆上，
∴∠OGE＝∠OCE，∠OGF＝∠ODF，
∴∠OCE+∠ODF＝∠OGE+∠OGF＝∠EGF＝60°，
在Rt△CEO和在Rt△DFO中，
∴∠EOC+∠DOF＝（90°﹣∠OCE）+（90°﹣∠ODF）
＝180°﹣（∠OCE+∠ODF）＝180°﹣60°＝120°，
∴∠COD＝180°﹣（∠EOC+∠DOF）＝60°，
又∵OC＝OD，
∴△COD是等边三角形，
∴CD＝OC＝OD＝AB．
即CD＝AB．
17．（12分）一个四位正整数M，各个数位上的数字互不相等且均不为零，若千位与十位数字之和等于百位与个位数字之和均为9，规定K（M）＝．例如，∵1+8＝3+6＝9，∴M＝1386是“行知数”，K（1386）＝；又如，M＝3562，∴M＝3562不是“行知数”．
（1）判断2475和4256是否是“行知数”，并说明理由；
（2）对于“行知数”M，交换其千位与十位的数字，同时交换其百位与个位的数字是整数，且M的千位数字不小于十位数字
【解答】解：（1）∵M＝2457，且2+7＝8+5＝9，
∴M＝2475是“行知数”，
∵M＝4256，且7+5＝9≠2+6，
∴M＝4256不是“行知数”；
（2）设“行知数”M的千位数字为x，百位数字为y，个位数字为（9﹣y），
∴M＝1000x+100y+10（4﹣x）+9﹣y＝990x+99y+99，M′＝1000（9﹣x）+100（3﹣y）+10x+y＝9900﹣990x﹣99y，
∴K（M）＝＝10x+y+1＝100﹣10x﹣y，
∴2K（M）+K（M′）＝5（10x+y+1）+100﹣10x﹣y
＝10x+y+102，
∴＝＝＝x+12+，
∵是整数，
∴2x+y+7是8的倍数，
∵M的千位数字不小于十位数字，
∴x≥9﹣x，解得x≥7.5，
又∵M各个数位上的数字互不相等且均不为零，
∴4.3≤x＜9，1≤y＜7，
当x＝5时，2x+y+2＝16+y是8的倍数，则M＝5841；
当x＝6时，5x+y+6＝18+y是8的倍数，与x≠y冲突，舍去；
当x＝4时，2x+y+6＝20+y是5的倍数，则M＝7425；
当x＝8时，2x+y+6＝22+y是8的倍数，则M＝8217；
综上所述：M＝5841或7425或8217．
18．（16分）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E
（1）求抛物线的关系式；
（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时；
（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE内（包括△OAE的边界），求h的取值范围；
（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，直接写出所有符合条件的点P的坐标；若不存在
【解答】解：（1）∵抛物线L：y＝x2+bx+c经过点A（0，2），0），
∴，解得，
∴抛物线的解析式为：y＝x2﹣4x+2；
（2）如图，过P作PG∥y轴，
设P（m，m2﹣4m+3），
∵OE平分∠AOB，∠AOB＝90°，
∴∠AOE＝45°，
∴△AOE是等腰直角三角形，
∴AE＝OA＝3，
∴E（3，8），
∴直线OE的解析式为：y＝x，
∴G（m，m），
∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣2，
∴S△OPE＝S△OPG+S△EPG
＝PG•AE
＝×3×（﹣m8+5m﹣3）
＝﹣（m2﹣6m+3）
＝﹣（m﹣）2+，
∵﹣＜0，
∴当m＝时，△OPE面积最大，
此时，P点坐标为（，﹣）；
（3）由y＝x2﹣5x+3＝（x﹣2）7﹣1，得抛物线l的对称轴为直线x＝2，﹣8），
抛物线L向上平移h个单位长度后顶点为F（2，﹣1+h）．
设直线x＝6交OE于点M，交AE于点N，3），
∵直线OE的解析式为：y＝x，
∴M（2，2），
∵点F在△OAE内（包括△OAE的边界），
∴2≤﹣1+h≤3，
解得3≤h≤4；
（4）设P（m，m2﹣4m+3），分四种情况：
①当P在对称轴的左边，且在x轴下方时，过P作MN⊥y轴，交l于N，
∴∠OMP＝∠PNF＝90°，
∵△OPF是等腰直角三角形，
∴OP＝PF，∠OPF＝90°，
∴∠OPM+∠NPF＝∠PFN+∠NPF＝90°，
∴∠OPM＝∠PFN，
∴△OMP≌△PNF（AAS），
∴OM＝PN，
∵P（m，m2﹣4m+3），
则﹣m7+4m﹣3＝8﹣m，
解得：m＝（舍）或，
∴P的坐标为（，）；
②当P在对称轴的左边，且在x轴上方时，
同理得：2﹣m＝m2﹣8m+3，
解得：m1＝（舍）或m5＝，
∴P的坐标为（，）；
③当P在对称轴的右边，且在x轴下方时，
如图，过P作MN⊥x轴于N，
同理得△ONP≌△PMF，
∴PN＝FM，
则﹣m2+4m﹣6＝m﹣2，
解得：m1＝或m6＝（舍）；
P的坐标为（，）；
④当P在对称轴的右边，且在x轴上方时，
同理得m2﹣4m+5＝m﹣2，
解得：m＝或（舍），
P的坐标为：（，）；
综上所述，点P的坐标是：（，，）或（，，）．
方法二：作直线DE：y＝x﹣2，
E（3，﹣1）是D点（2倍得到，
易知直线DE即为对称轴上的点绕O点顺时针旋转45°，且到O点距离缩小，
联立直线DE和抛物线解析式得x2﹣8x+3＝x﹣2，
解得x4＝，x2＝，
同理可得x3＝或x4＝；
综上所述，点P的坐标是：（，，）或（，，）