
初中数学浙教版七年级下册2.4 二元一次方程组的应用教案
展开课题
2.4 解二元一次方程组(1)
单元
第二单元
学科
数学
年级
七年级下册
学习
目标
利用二元一次方程组解决面积问题、产品配套、和差倍分、行程等问题.
会用列表、画线段图等手段帮助分析理解实际问题.
重点
会用列方程组解决实际问题.
难点
在实际问题中找等量关系、列方程组.[
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
一.创设情景,引出课题
合作学习
(1)今有鸡兔同笼,上有35头,下有94足,问鸡兔各有多少头?
1、问题中有几个未知数?
2、问题中可以得到几个等量关系式?
3、你准备设哪几个未知数?
4、你能列出方程或方程组吗?
解:设共有x只鸡,则共有(35-x)只兔子。
根据题意,得
2x+4(35-x)=94。
解这个方程,得x=23。
∴ 35-x=35-23=12。
答:共有23只鸡,12只兔子。
列一元一次方程解应用题的一般步骤:
1、审题;
2、找出一个等量关系式;
3、设元并列出方程;
4、解方程并求出相关的量;
5、写出答案。
解:设共有x只鸡,y只兔。
根据题意,得
x+y=35
2x+4y=94
解这个方程组,得
x=23
y=12
答:共有23只
(2)游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽。如果每位男孩看到蓝色与红色的游泳帽一样多,而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
鸡,12只兔子。
思考下面几个问题:
1.问题中的未知数有几个?
2.有哪些等量关系?
3.怎样设未知数?可以列几个方程?
4.本题能列一元一次方程吗?用列二元一次方程组的方法求解,有什么优点?
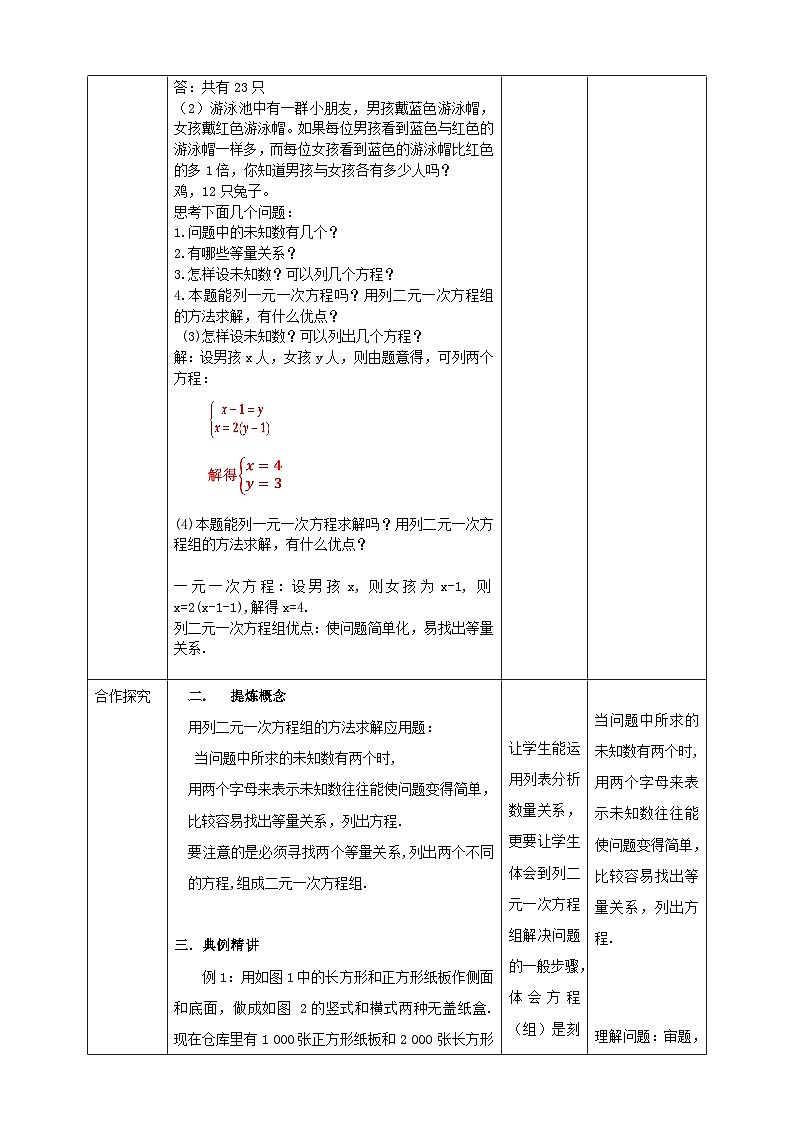
(3)怎样设未知数?可以列出几个方程?
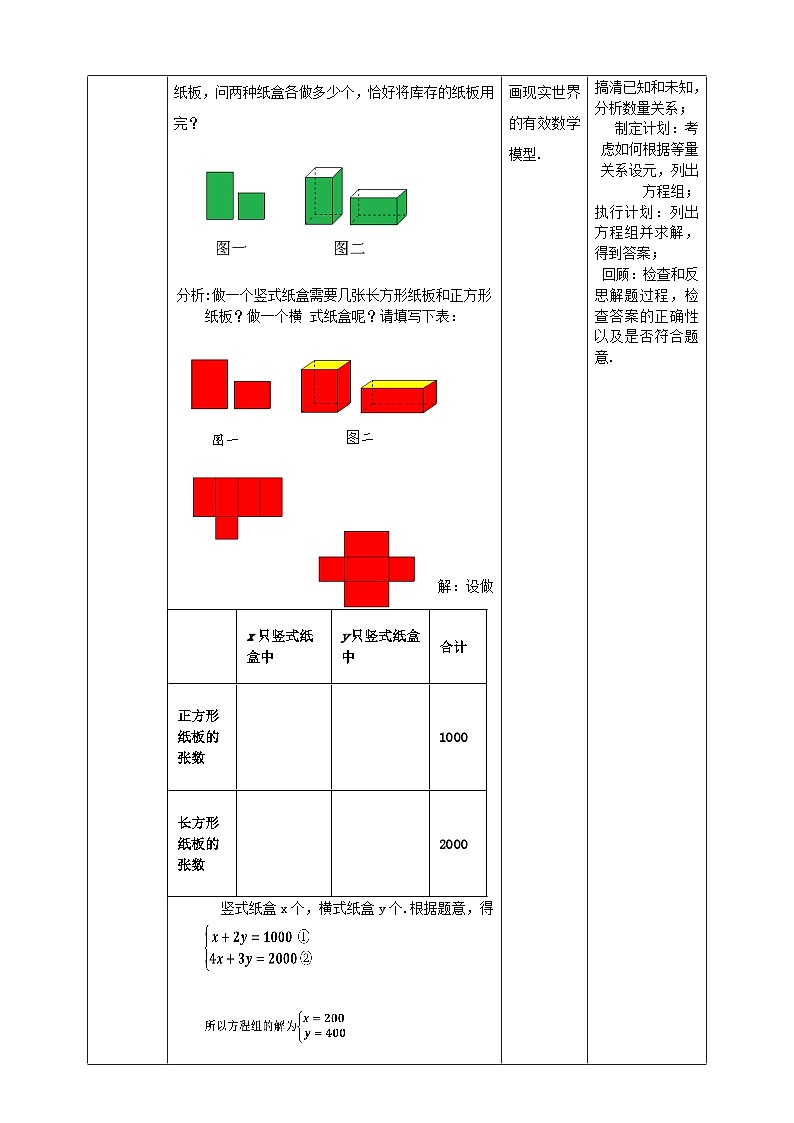
解:设男孩x人,女孩y人,则由题意得,可列两个方程:
(4)本题能列一元一次方程求解吗?用列二元一次方程组的方法求解,有什么优点?
一元一次方程:设男孩x,则女孩为x-1,则x=2(x-1-1),解得x=4.
列二元一次方程组优点:使问题简单化,易找出等量关系.
思考
自议
二元一次方程组在实际生活中的应用,关键是找相等关系.
熟悉各种类型的相等关系,是列方程的关键.
合作探究
提炼概念
用列二元一次方程组的方法求解应用题:
当问题中所求的未知数有两个时,
用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
要注意的是必须寻找两个等量关系,列出两个不同的方程,组成二元一次方程组.
三.典例精讲
例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图 2的竖式和横式两种无盖纸盒. 现在仓库里有1 000张正方形纸板和2 000 张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?
分析:做一个竖式纸盒需要几张长方形纸板和正方形纸板?做一个横 式纸盒呢?请填写下表:
图一
图二
x只竖式纸盒中
y只竖式纸盒中
合计
正方形纸板的张数
1000
长方形纸板的张数
2000
解:设做竖式纸盒x个,横式纸盒y个.根据题意,得
经检验,这个解满足方程组,且符合题意.
答: 做竖式纸盒200个,横式纸盒400个,恰好纸板用完.
一般地,问题解决的基本步骤适用于二元一次方程组
解决实际问题:
理解问题:审题,搞清已知和未知,分析数量关系;
制定计划:考虑如何根据等量关系设元,列出方程组;
执行计划:列出方程组并求解,得到答案;
回顾:检查和反思解题过程,检查答案的正确性以及是否符合题意.
让学生能运用列表分析数量关系,更要让学生体会到列二元一次方程组解决问题的一般步骤,体会方程(组)是刻画现实世界的有效数学模型.
当问题中所求的未知数有两个时,用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
理解问题:审题,搞清已知和未知,分析数量关系;
制定计划:考虑如何根据等量关系设元,列出方程组;
执行计划:列出方程组并求解,得到答案;
回顾:检查和反思解题过程,检查答案的正确性以及是否符合题意.
当堂检测
巩固训练
某班共有学生49人.一天,该班某男生因事请假,当天的男生人数恰为女性人数的一半.若设该班男生人数为x,女生人数为y,则下列方程组中,能正确计算出x,y的是 ( )
A.eq \b\lc\{(\a\vs4\al\c1(x-y=49,,y=2(x+1))) B.eq \b\lc\{(\a\vs4\al\c1(x+y=49,,y=2(x+1)))
C.eq \b\lc\{(\a\vs4\al\c1(x-y=49,,y=2(x-1))) D.eq \b\lc\{(\a\vs4\al\c1(x+y=49,,y=2(x-1)))
【解析】 本题考查方程组在实际生活中的应用.列方程组的等量关系是:(1)男生数+女生数=49人.(2)男生数-1=女生数的一半.选D
2. 如图,用8块相同的长方形地砖拼成了一个矩形图案(地砖间的缝隙忽略不计),则每块地砖的长和宽分别为( )
A.50,10 B.45,15
C.40,20 D.35,25
【解析】 设地砖的长为a,宽为b.
根据图形,得eq \b\lc\{(\a\vs4\al\c1(a+b=60,,2a=3b+a.))
解得a=45,b=15.选B.
3.车间有28名工人参加生产某种特制的螺丝和螺母,已知平均每人每天能生产螺丝12个或螺母18个,一个螺丝将配两个螺母.问:应怎样安排生产螺丝和螺母的工人,才能使每天的产品正好配套?
解:设每天安排x人生产螺丝,y人生产螺母,那么每天能产生螺丝12x个,螺母18y个.
根据题意,得eq \b\lc\{(\a\vs4\al\c1(x+y=28,,12x∶18y=1∶2.))
解得eq \b\lc\{(\a\vs4\al\c1(x=12,,y=16.))
答:应安排12人生产螺丝,16人生产螺母.
【点悟】配套问题的解题关键是要了解哪种数量多,哪种数量少,是几比几的配合问题,了解倍数关系.
4.A,B两地相距20千米,甲、乙两人分别从A、B两地同时相向而行,两小时后在途中相遇,然后甲返回A地,乙仍继续前进,当甲回到A地时,乙离A地还有2千米,求甲、乙的速度.
【解析】 这个问题是直线行驶中的相遇追击问题,其中有两个未知数:甲、乙各自的速度,有两个相等关系,即(1)相向而行:甲、乙的行程和=20 千米.(2)同向而行:甲的行程-乙的行程=2千米.设未知数,列方程组求解.
解:设甲的速度是每小时行x千米,乙的速度是每小题行y千米.依题意,得eq \b\lc\{(\a\vs4\al\c1(2(x+y)=20,,2x-2y=2.))
解得eq \b\lc\{(\a\vs4\al\c1(x=5.5,,y=4.5.))
答:甲的速度是5.5千米/时,乙的速度是4.5千米/时.
课堂小结
应用二元一次方程组解决实际问题的基本步骤:
理解问题:审题,搞清已知和未知,分析数量关系;
制订计划:考虑如何根据等量关系设元,列出方程组;
执行计划:列出方程组并求解,得到答案.
回顾:检查和反思解题过程,检验答案的正确性以及是否符合题意.
初中浙教版2.4 二元一次方程组的应用教案: 这是一份初中浙教版<a href="/sx/tb_c12142_t8/?tag_id=27" target="_blank">2.4 二元一次方程组的应用教案</a>,共3页。教案主要包含了教学目标,教学重点、难点,教学过程等内容,欢迎下载使用。
初中数学浙教版七年级下册2.4 二元一次方程组的应用教案及反思: 这是一份初中数学浙教版七年级下册2.4 二元一次方程组的应用教案及反思,共6页。教案主要包含了引入,新课,当堂练,归纳总结,作业,反思等内容,欢迎下载使用。
初中鲁教版 (五四制)3 二元一次方程组的应用第1课时教案及反思: 这是一份初中鲁教版 (五四制)3 二元一次方程组的应用第1课时教案及反思,共2页。













