河南省信阳市潢川县2022-2023学年八年级下学期期中考试数学试卷(含答案)

这是一份河南省信阳市潢川县2022-2023学年八年级下学期期中考试数学试卷(含答案)，共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下列二次根式是最简二次根式的是( )
A.B.C.D.
2．已知四边形是平行四边形，、相交于点O，下列结论错误的是( )
A.B.C.D.
3．下列运算正确的是( )
A.B.C.D.
4．如图，在菱形中，对角线与相交于点O，，，则该菱形的边长是( )
A.5B.C.6D.10
5．如图，阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形.已知，，则( )
A.B.C.D.4
6．的倒数是( )
A.B.C.D.
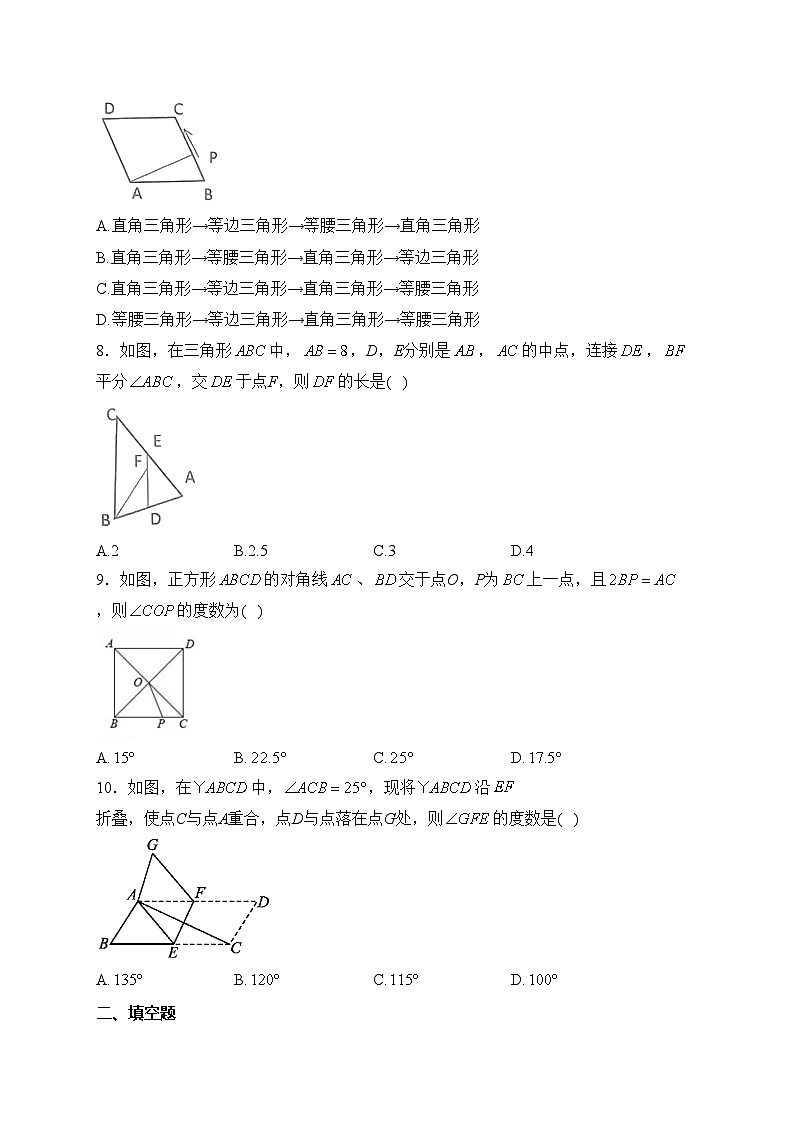
7．如图，菱形中，，点P从点B出发，沿折线方向移动，移动到点D停止.在三角形形状的变化过程中，依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
8．如图，在三角形中，，D，E分别是，的中点，连接，平分，交于点F，则的长是( )
A.2B.2.5C.3D.4
9．如图，正方形的对角线、交于点O，P为上一点，且，则的度数为( )
A.B.C.D.
10．如图，在中，，现将沿折叠，使点C与点A重合，点D与点落在点G处，则的度数是( )
A.B.C.D.
二、填空题
11．要使有意义，则x的取值范围为__________.
12．如图，平面直角坐标系中，点A，B的坐标分别为和，以A为圆心，长为半径画弧，交x轴的正半轴于点C，则点C的横坐标是__________.
13．已知正方形的边长为8，点E，F分别在，上，，与相交于点G，H为的中点，连接，则的长为__________.
14．如图所示的赵爽弦图是由四个全等的直角三角形和小正方形拼的大正方形.如果直角三角形中较短的直角边长为a，较长的直角边长为b，大正方形的边长是，，那么__________.
15．已知A、B、C三点的坐标分别为，，，若以A，B，C，D为顶点的四边形是平行四边形，则点D的坐标是__________.
三、解答题
16．计算
（1）；
（2）.
17．如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点.
（1）图1中的顶点都在格点上，判断它的形状，并说明理由；
（2）在图2中画一个面积为10的正方形，使它的顶点都在格点上.
18．如图，一艘船由A港沿北偏东方向航行至B港，然后再沿北偏西方向航行至C港.
（1）求A，C两港之间的距离（结果保留到，参考数据：，）；
（2）确定C港在A港的什么方向.
19．观察下列各式及其变形过程：
……
（1）按照此规律写出第五个等式_____________.
（2）按照此规律，若，当时，____________.
（3）在（2）的条件下，若，试求x的值.
20．如图，在平行四边形中，平分，平分.
（1）求证，.
（2）当满足什么条件时，四边形是矩形？请写出证明过程.
21．（1）我们在本学期已学习定理：直角三角形斜边上的中线等于斜边的一半.请你利用矩形的性质，证明该定理.
已知：如图1，在中，，是的中点：
求证：_______________________
证明：
（2）如图2，四边形中，，，E，F分别是，的中点，连接，，，求证：.
22．如图1，将一张矩形纸片沿着对角线向上折叠，顶点C落到点E处，交于点F.
（1）求证：是等腰三角形.
（2）如图2，过点D作交于点G，连接交于点O.
①判断四边形的形状，并说明理由.
②若，，求的长.
23．如图，将正方形放置在平面直角坐标系中，点B与原点重合，点A的坐标.
（1）直接写出D点的坐标.
（2）E点在x轴正半轴上，连接，过E点做交正方形外角平分线于点F.
①当E在正方形边上时，求证：.
②当E在边上的延长线上时，试㮠究与之间的数量关系，并说明理由.
③若E点坐标为，试用含a的式子直接表示出的面积.
参考答案
1．答案：C
解析：A.，故不是最简二次根式；
B.，故不是最简二次根式；
C.，是最简二次根式；
D.，故不是最简二次根式.
故选C.
2．答案：B
解析：四边形ABCD是平行四边形，
，，
，
选项A、C、D、正确，B不一定正确，
故选B.
3．答案：D
解析：A.、被开方数不，不能合并，本选项不合题意；
B.，本选项不合题意；
C.，本选项不合题意；
D.计算正确，本选项符合题意.
故选D.
4．答案：A
解析：四边形是菱形，，，
，，，
，
故选A.
5．答案：D
解析：，，
，
半圆BC面积+半圆AC面积-半圆AB面积
故选D.
6．答案：D
解析：，
的倒数为.
故选D.
7．答案：C
解析：当时，为直角三角形；
当点P到达点C处时，为等边三角形；
当点P是CD的中点时，为等腰三角形；
当点P与点D重合时，为等腰三角形.
故选C.
8．答案：D
解析：D，F分别是AB，AC的中点，
，，
平分，
，
，
，
故选D.
9．答案：B
解析：四边形ABCD是正方形，
，，，
，
，
，
，
故选B.
10．答案：C
解析：由折叠的性质可得，，，
，
，
，
四边形ABCD是平行四边形，
，
，
，
，
故选C.
11．答案：
解析：由有意义，
，
解得，
故答案为.
12．答案：
解析：点A，B的坐标分别为，，
，，
，
以A为圆心，AB长为半径画弧，
，
，
交x轴正半轴于点C，
点C的横坐标是，
故答案为.
13．答案：5
解析：因为四边形ABCD为正方形，
，，
在和中
，
，
，
，
，
则，
，
则，
正方形边长为8，，
，，
，
点H为BF的中点，
，
故答案为5.
14．答案：20
解析：由题意可知:大正方形的边长为：，
直角三角形边长分别为a，b，
根据股定理可得：，
又，
可得，，
，
故答案为：20.
15．答案：，，
解析：当以BC为对角线时，
，
，
当以AC为对角线时，
，
，
当以AB为对角线时，
，
，
综上所述，点D的坐标是，，，
故答案为，，.
16．答案：（1）
（2）
解析：（1）
；
（2）
.
17．答案：（1）是直角三角形，理由见解析
（2）见解析
解析：（1）是直角三角形，
，，，
，
是直角三角形
（2）画图如下：
18．答案：（1）A、C两地之间的距离为
（2）C港在A港北偏东15°的方向上
解析：（1）由题意可得，，，
，，
，
，
，
∴.
答：A、C两地之间的距离为.
（2）由（1）知，为等腰直角三角形，
，
，
C港在A港北偏东15°的方向上.
19．答案：（1）
（2）
（3）
解析：（1）
（2）
（3），
.
20．答案：（1）见解析
（2）当满足时，四边形是矩形
解析：（1）证明：四边形是平行四边形，
，，，
，
平分、平分，
，
，
，
在和中，
，
；
（2）当满足时，四边形是矩形，理由如下：
由（1）可知，，
，
，
，
四边形是平行四边形，
又，平分，
，
，
平行四边形是矩形.
21．答案：（1）见解析
（2）见解析
解析：（1）求证.
证明：延长至点D，使，连接，，
O是的中点，
，
四边形是平行四边形，
，
平行四边形是矩形，
，
；
（2），E是的中点.
，
F是的中点，
是三角形的中位线，
，
，
，
.
22．答案：（1）见解析
（2）①四边形是菱形，理由见解析
②
解析：（1）证明，根据折叠的性质得，，
，
，
，
，
是等腰三角形
（2）①四边形是菱形，理由如下，
四边形是矩形.
，
又
四边形是平行四边形,
四边形是菱形；
②，，
，，
设，则，
在中，即，
解得即，
，
.
23．答案：（1）
（2）①见解析
②，理由见解析
③或
解析：（1）
（2）①证明：如图，在上截取等于.连接，
四边形是正方形，
，，
，，，
是外角的平分线，
，
，
，
，
，
，
；
②，
理由如下：延长至G使连接，
四边形是正方形，
，，，
，
，
是外角的平分线，
，，
，，
，
，
，
；
③或.