2024年福建省顺昌县部分学校中考一模数学试题（原卷版+解析版）

这是一份2024年福建省顺昌县部分学校中考一模数学试题（原卷版+解析版），文件包含2024年福建省顺昌县部分学校中考一模数学试题原卷版docx、2024年福建省顺昌县部分学校中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
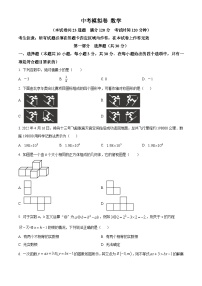
一、选择题（每小题4分，共40分）
1. 下列计算结果是正数的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了正数，有理数的加减运算．熟练掌握正数，有理数的加减运算是解题的关键．
对各选项进行计算，然后判断作答即可．
【详解】解：A、，结果是负数，故不符合要求；
B、，结果是正数，故符合要求；
C、，结果是负数，故不符合要求；
D、，结果是负数，故不符合要求；
故选：B．
2. 2023年福建省GDP的增量为亿元．将亿用科学记数法表示应为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查用科学记数法表示绝对值大于1的数．科学记数法的表示形式为的形式，其中为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．熟记相关结论即可．
【详解】解：∵亿
故选：C
3. 如图是一个立体图形的三视图，该立体图形是（ ）

A. 圆柱B. 圆锥C. 棱柱D. 球
【答案】A
【解析】
【分析】本题考查了由三视图还原几何体，旨在考查学生的空间想象能力．
【详解】解：A：圆柱的三视图分别为：矩形、矩形、圆，符合题意；
B：圆锥的三视图没有矩形，不符合题意；
C：棱柱的三视图没有圆，不符合题意；
D：球的三视图均为圆，不符合题意；
故选：A
4. 下列既是轴对称图形又是中心对称图形的是（ ）
A. 直角B. 等边三角形C. 菱形D. 扇形
【答案】C
【解析】
【分析】根据“沿一条直线折叠，直线两旁的部分能够完全重合的平面图形叫做轴对称图形；绕某一点旋转，旋转后的图形能与原图形重合，那么这个图形是中心对称图形
”进行判断即可．
【详解】解：直角是轴对称图形，不是中心对称图形，故A不符合题意；
等边三角形是对称轴图形，不是中心对称图形，故B不符合题意；
菱形既是轴对称图形，也是中心对称图形，故C符合题意；
扇形是轴对称图形，不是中心对称图形，故D不符合题意；
故选：C．
5. 不等式的解集在数轴上表示正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查解不等式，并在数轴上表示不等式的解集．
先解不等式，再根据不等式在数轴上的表示方法求解即可．
【详解】解：，
解得，，
把不等式的解集在数轴上表示如下：
故选：A．
6. 下列计算结果正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】此题主要考查了合并同类项以及单项式的乘除法，正确掌握相关运算法则是解题关键．直接利用合并同类项法则以及单项式的乘除法则分别判断得出答案．
【详解】解：A、和不是同类项，无法合并，故此选项错误；
B、和不是同类项，无法合并，故此选项错误；
C、，故此选项正确；
D、，故此选项错误；
故选：C．
7. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋，设货架上原有鸡蛋的质量（单位：g）平均数和方差分别为，s2，该顾客选购的鸡蛋的质量平均数和方差1，，则下列结论一定成立的是（ ）
A. 1B. 1C. s2＞D. s2
【答案】C
【解析】
【分析】根据平均数和方差的意义，即可得到答案．
【详解】解：∵顾客从一批大小不一的鸡蛋中选购了部分大小均匀的鸡蛋，
∴＜s2，和1的大小关系不明确，
故选C
【点睛】本题主要考查平均数和方差的意义，掌握一组数据越稳定，方差越小，是解题的关键．
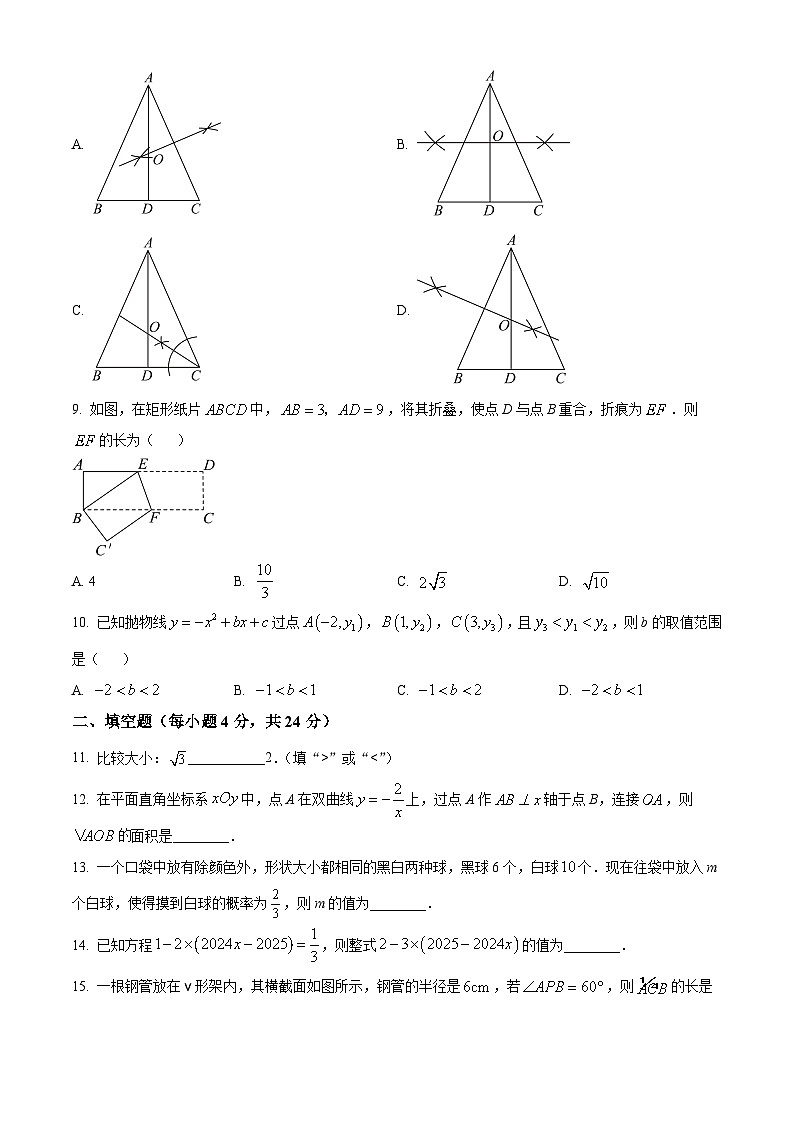
8. 如图，已知，，是高，用尺规作图的方法作出的内心O，则下列作图正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题主要考查了三角形的内心问题，等腰三角形的性质．根据等腰三角形的性质可得平分，再由三角形的内心定义，即可求解．
【详解】解：∵，是高，
∴平分，
∴要用尺规作图的方法作出的内心O，只需作出或的角平分线，即可．
故选：C
9. 如图，在矩形纸片中，，将其折叠，使点D与点B重合，折痕为．则的长为（ ）
A. 4B. C. D.
【答案】D
【解析】
【分析】由折叠的性质，矩形的性质可知，，，则，设，则，由勾股定理得，，即，可求，则，如图，作于，则四边形是矩形，，，由勾股定理得，，计算求解即可．
【详解】解：由折叠的性质可知，，，
∵矩形，
∴，
∴，
∴，
设，则，
由勾股定理得，，即，
解得，，
∴，
如图，作于，则四边形是矩形，
∴，
∴，
由勾股定理得，，
故选：D．
【点睛】本题考查了矩形与折叠，等角对等边，矩形的判定与性质，勾股定理等知识．熟练掌握矩形与折叠，等角对等边，矩形的判定与性质，勾股定理是解题的关键．
10. 已知抛物线过点，，，且，则b的取值范围是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查了二次函数图象上点的坐标特征．熟练掌握抛物线的对称性和增减性，开口方向，是解决问题的关键．
根据抛物线的开口向下，对称轴是直线，得到抛物线上的点离对称轴越近，对应的函数值就越大，由，，，知，与在对称轴两侧，可得，解此不等式即得．
【详解】∵抛物线开口向下，对称轴是直线，
∴抛物线上点离对称轴越近，对应的函数值就越大，
∵，
∴离对称轴最近，次之，离对称轴最远，
且与在对称轴两侧，
∴对称轴在直线和之间，
即，
∴．
故选：．
二、填空题（每小题4分，共24分）
11. 比较大小：___________2．（填“>”或“