北师大版（2021）拓展模块一 上册2.4.2 余弦定理完美版ppt课件

这是一份北师大版（2021）拓展模块一 上册2.4.2 余弦定理完美版ppt课件，文件包含北师大版《中职数学拓展模块一上册》第16课余弦定理课件pptx、北师大版《中职数学拓展模块一上册》第16课余弦定理教学设计docx等2份课件配套教学资源，其中PPT共14页， 欢迎下载使用。

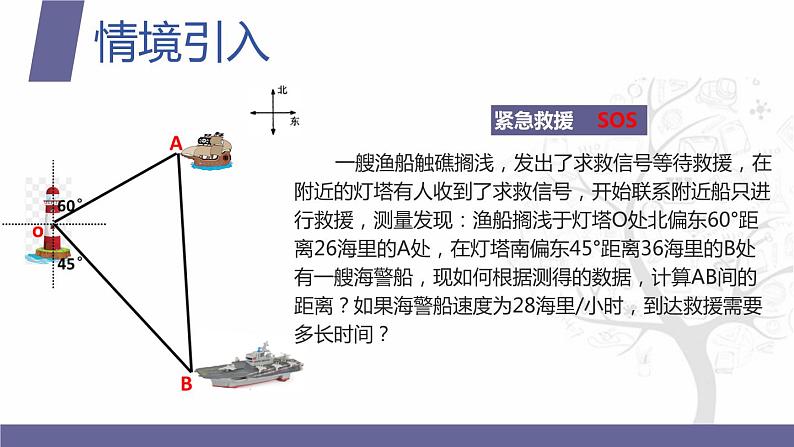
紧急救援 SOS
一艘渔船触礁搁浅，发出了求救信号等待救援，在附近的灯塔有人收到了求救信号，开始联系附近船只进行救援，测量发现：渔船搁浅于灯塔O处北偏东60°距离26海里的A处，在灯塔南偏东45°距离36海里的B处有一艘海警船，现如何根据测得的数据，计算AB间的距离？如果海警船速度为28海里/小时，到达救援需要多长时间？
可以证明，对于任意三角形上述结论都成立
三角形中任意一边的平方等于其余两边的平方和减这两边与其夹角余弦乘积的两倍.
备注：观察余弦定理公式的结构特征，辅助记忆。另外，公式中共有四个变量,我们可以知三求一，利用余弦定可 以解决“在三角形中，已知两边及其夹角，求其他元素”的问题.
这个结论(边、角关系) 称为余弦定理.
余弦定理经变形也可以写成
如何利用三角形三条边长求解三角形内角的角度大小？
总结：利用余弦定理解三角形，主要适用于以下两种情形.(1)已知三角形的两条边和它们的夹角，求第三边和其余两个角；(2)已知三角形的三边，求三个角.
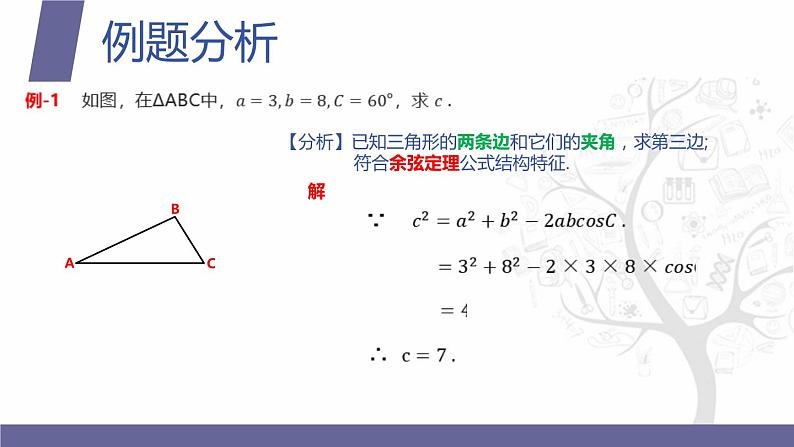
【分析】已知三角形的两条边和它们的夹角，求第三边; 符合余弦定理公式结构特征.
【分析】已知三角形的三边，求三个角;符合余弦定理变形公式结构特征.
(1) 证明：三角形为钝角三角形；(2) 求三角形的最大内角.
备注：可以借助（Casi）计算器计算求值；
【分析】已知三角形的两条边和它们的夹角，求第三边、角度;符合余弦定理公式结构特征.
②余弦定理解三角形情形：
(a)已知三角形的两条边和它们的夹角，求第三边和其余两个角；(b)已知三角形的三边，求三个角.