江苏省宿迁市沭阳县乡镇联考2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版）

这是一份江苏省宿迁市沭阳县乡镇联考2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版），文件包含江苏省宿迁市沭阳县乡镇联考2023-2024学年八年级下学期3月月考数学试题原卷版docx、江苏省宿迁市沭阳县乡镇联考2023-2024学年八年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

一、选择题（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案填涂在答题卡相应的位置上．）
1. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录．北京国际设计周面向社会公开征集“二十四节气”标识系统设计，以期通过现代设计的手段，尝试推动我国非物质文化遗产创新传承与发展．下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是中心对称图形的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查中心对称图形的识别，根据中心图形的概念求解即可．
【详解】解：A、不是中心对称图形，本选项错误，不符合题意；
B、不是中心对称图形，本选项错误，不符合题意；
C、不是中心对称图形，本选项错误，不符合题意；
D、是中心对称图形，本选项正确，符合题意．
故选：D
2. 今年某市有8万多名学生参加中考，为了了解这些考生的数学成绩，从中抽取2000名考生的数学成绩进行统计分析．在这个问题中，下列说法：①这8万名考生的数学中考成绩的全体是总体：②每个考生是个体：③2000名考生是总体的一个样本：④样本容量是2000．其中说法正确的有（ ）
A. 4个B. 3个C. 2个D. 1个
【答案】C
【解析】
【分析】本题是总体、个体、样本、样本容量的问题，根据总体、个体、样本、样本容量的定义； 解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小，由此判断出①②③是否正确； 样本容量是样本中包含的个体的数目，不能带单位，由此判断④是否正确．
【详解】解：①这8万名考生的数学中考成绩的全体是总体，正确；
②每个考生的数学中考成绩是个体，原说法错误；
③2000名考生的数学成绩是总体的一个样本，原说法错误；
④样本容量是2000，正确．
故选：C
3. 下列事件：①检查生产流水线上的一个产品，是合格品；
②三条线段组成一个三角形；
③a是实数，则；
④一副扑克牌中，随意抽出一张是红桃；
⑤个人中至少有个人生日相同：
⑥一个抽奖活动的中奖率是，参与抽奖次，就一定会中奖，其中属于必然事件的个数是( )
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】本题考查了必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．根据定义即可判断．
【详解】解：①②④⑥是随机事件；
③是不可能事件，是确定事件；
⑤是必然事件，是确定事件．
故选：A．
4. 已知：四边形ABCD的对角线AC、BD相交于点O，则下列条件不能判定四边形ABCD是平行四边形的是
A. ，B. ，
C. ，D. ，
【答案】B
【解析】
【分析】平行四边形的判定定理:(1)两组对边分别平行的四边形是平行四边形,(2)两组对边分别相等的四边形是平行四边形,(3)一组对边平行且相等的四边形是平行四边形,(4)两组对角分别相等的四边形是平行四边形,(5)对角线互相平分的四边形是平行四边形,根据平行四边形的判定即可解答.
【详解】A选项, ,,根据两组对边分别平行的四边形是平行四边形,能判定四边形ABCD是平行四边形,
B选项 ,不能判定四边形是平行四边形,
C选项,,根据对角线互相平分的四边形是平行四边形,能判定四边形ABCD是平行四边形,
D选项,,根据两组对角分别相等的四边形是平行四边形能判定四边形ABCD是平行四边形,
故选B.
【点睛】本题主要考查平行四边形的判定定理,解决本题的关键是要熟练掌握平行四边形的判定定理.
5. 如图，矩形ABCD的对角线AC＝8cm，∠AOD＝120º，则AB的长为( )
A. 1cmB. 2cmC. 3cmD. 4cm
【答案】D
【解析】
【分析】根据矩形性质，证是等边三角形，，进而可得的值．
【详解】解：由矩形的性质可知， ，
∵，
∴
∴是等边三角形.
∴
故选D．
【点睛】本题考查了矩形的性质，等边三角形的判定与性质，平角等知识．解题的关键在于对知识的灵活运用．
6. 如图，在中，，D，E，F分别为，，中点，若，则的长度是（ ）

A. B. 1C. D.
【答案】A
【解析】
【分析】本题考查了直角三角形斜边中线的性质，含直角三角形的性质，三角形中位线定理；
根据直角三角形斜边中线的性质和含直角三角形的性质求出，再根据三角形中位线定理即可求出的长度．
【详解】解：∵在中，点D为斜边中点，，
∴，
∵为的中位线，
∴，
故选：A．
7. 牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于时，第一步先假设（ ）
A. 三角形中有一个内角小于B. 三角形中有一个内角大于
C. 三角形中每个内角都大于D. 三角形中没有一个内角小于
【答案】C
【解析】
【分析】根据反证法的步骤中，第一步是假设结论不成立，反面成立解答．
【详解】解：用反证法证明：在一个三角形中，至少有一个内角小于或等于时，
第一步先假设三角形中每个内角都大于，
故选：C．
【点睛】本题考查的是反证法，解此题关键要懂得反证法的意义及步骤．反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．
8. 如图，点E为正方形内一点，，将绕点B按顺时针方向旋转，得到．延长交于点F，连接．下列结论：①；②四边形是正方形；③若，则；其中正确的是（ ）

A. ①②③B. ①②C. ②③D. ①
【答案】A
【解析】
【分析】设交于K，由及将绕点B按顺时针方向旋转，得到，可得，即可得，从而判断①正确；由旋转的性质可得，，，由正方形的判定可证四边形是正方形，可判断②正确；过点D作于H，由等腰三角形的性质可得，，由“”可得，可得，由旋转的性质可得，从而可得，判断③正确．
【详解】解：设交于K，如图：

∵四边形是正方形，
∴，
∴，
∵将绕点B按顺时针方向旋转，得到，
∴，
∵，
∴，
∴，
∴，故①正确；
∵将绕点B按顺时针方向旋转，
∴，，，
又∵，
∴四边形是矩形，
又∵，
∴四边形是正方形，故②正确；
如图，过点D作于H，

∵，，
∴，
∴，
∵四边形是正方形，
∴，，
∴，
∴，
又∵，，
∴，
∴，
∵将绕点B按顺时针方向旋转，
∴，
∵四边形是正方形，
∴，
∴，
∴，故③正确；
∴正确的有：①②③，
故选：A．
【点睛】本题是四边形综合题，考查了正方形的判定和性质，旋转的性质，全等三角形的判定和性质等知识，灵活运用这些性质进行推理是本题的关键．
二、填空题（本大题共10小题，每小题3分，共30分．不需要写出解答过程，请把答案直接填写在答题卡相应位置上）
9. 为了解某校八年级名学生每天的阅读时间，从中抽取了名学生进行调查，在这个问题中，样本容量是_______．
【答案】
【解析】
【分析】本题主要考查了样本容量，根据样本容量的定义，是指样本中个体的数目．
【详解】解：这个问题中，样本容量是．
故答案为：．
10. 走入考场之前老师送你一句话“”．在这句话中任选一个字母，这个字母为“”的概率是_______．
【答案】
【解析】
【分析】本题考查了概率公式求概率，根据题意得出共14个字母，其中有字母“c”2个，进而根据概率公式，进行计算即可求解．
【详解】解：在英语句子“”中共14个字母，
其中有字母“”2个；
故其概率为．
故答案为：．
11. 有40个数，共分成6组，第组的频数分别是10、5、7、6，若第5组的频率是，则第6组的频率是______．
【答案】##
【解析】
【分析】先求得第5组的频数，再求得第6组的频数，利用频数除以数据总数即可求解．
【详解】解：∵有40个数，第5组的频率是，
∴若第5组的频数是，
∴第6组的频数是，
∴第6组的频率是，
故答案为：．
【点睛】本题考查频数和频率，熟知频率=频数÷数据总数是解答的关键．
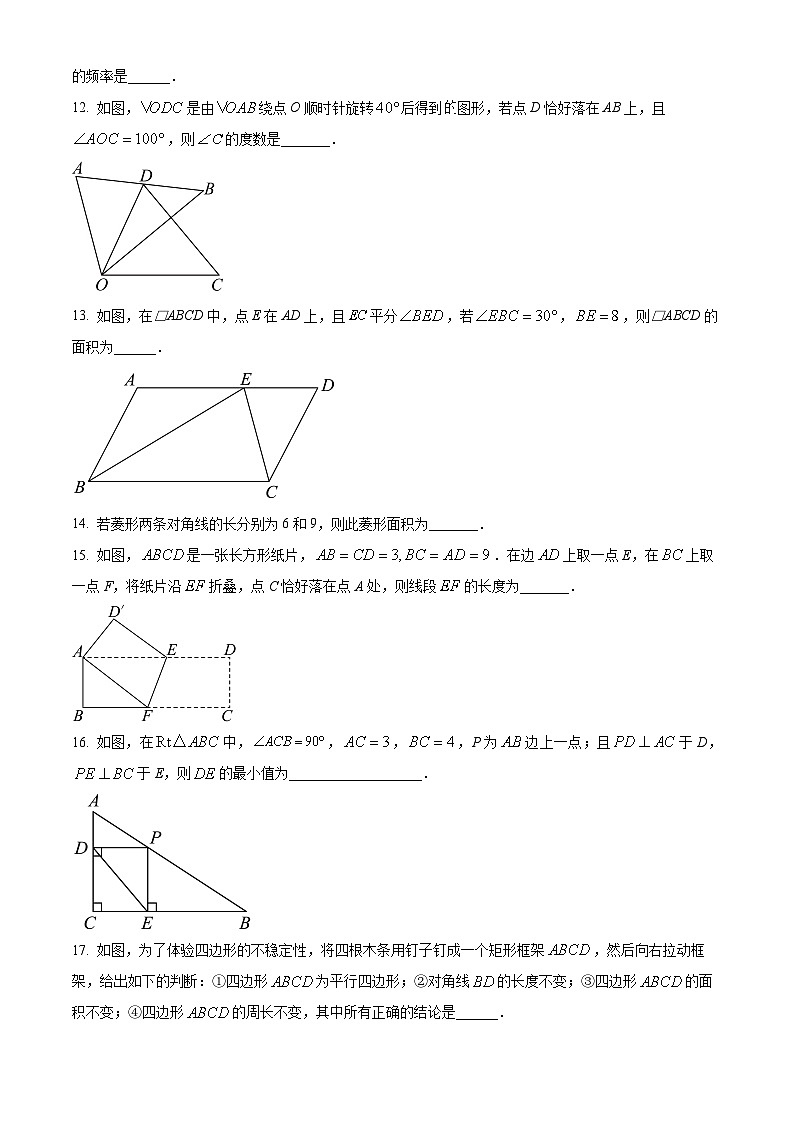
12. 如图，是由绕点O顺时针旋转后得到的图形，若点D恰好落在AB上，且，则的度数是_______．
【答案】##50度
【解析】
【分析】本题考查了旋转的性质、等腰三角形的性质、以及三角形内角和定理，掌握旋转的性质是解题的关键．根据旋转的性质可得，，再求出，及，即可知的度数，然后根据三角形的内角和定理即可求出的度数．
【详解】∵是绕点O顺时针旋转后得到图形，
∴，，
∵，
∴，
，
∴，
∴，
故答案为：．
13. 如图，在□ABCD中，点E在AD上，且平分，若，，则□ABCD的面积为______．
【答案】32
【解析】
【分析】过点E作，垂足为F，利用直角三角形的性质求出，再根据平行线的性质和角平分线的定义得到，可得，最后利用平行四边形的面积公式计算即可．
【详解】解：过点E作，垂足为F，
∵，
∴，
∵四边形ABCD是平行四边形，
∴，
∴，
又平分，即，
∴，
∴，
∴四边形的面积=，
故答案为：．
【点睛】本题考查了平行四边形的性质，30度的直角三角形的性质，角平分线的定义，等角对等边，作出辅助线构造直角三角形求出的长是解题的关键．
14. 若菱形两条对角线的长分别为6和9，则此菱形面积为_______．
【答案】
【解析】
【分析】本题考查菱形的性质，根据菱形的对角线互相垂直，互相垂直的四边形的面积等于对角线乘积的一半．
【详解】解：菱形的面积为：．
故答案为：．
15. 如图，是一张长方形纸片，．在边上取一点E，在上取一点F，将纸片沿折叠，点C恰好落在点A处，则线段的长度为_______．

【答案】
【解析】
【分析】本题主要考查了勾股定理，平行线的性质．等腰三角形的判定和性质，图形的折叠问题．过点F作于点G，则，，根据平行线的性质乙折叠的性质可得，从而得到，设，则，在中，根据勾股定理可得，从而得到，再由勾股定理，即可求解．
【详解】解：如图，过点F作于点G，则，，

根据题意得：，
∴，
由折叠的性质得：，，
∴，
∴，
设，则，
在中，，
∴，
解得：，
∴，
∴，
∴．
故答案为：
16. 如图，在中，，，，P为边上一点；且于D，于E，则的最小值为___________________．

【答案】####2.4
【解析】
【分析】由在中，，且于D，于E，易得四边形是矩形，然后连接，可得，即可得当时，最短，即最小，继而求得答案．
【详解】解：连接，如图所示：

∵，
∴，
∵在中，，
∴四边形是矩形，
∴，
∵，，
∴，
∵当时，最短，即最小，
∴．
故答案为：．
【点睛】此题考查了矩形的判定与性质以及垂线段最短的知识．注意准确作出辅助线是解此题的关键．
17. 如图，为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架，然后向右拉动框架，给出如下的判断：①四边形为平行四边形；②对角线的长度不变；③四边形的面积不变；④四边形的周长不变，其中所有正确的结论是______．

【答案】①④##④①
【解析】
【分析】根据平行四边形的判定和性质即可判断．
【详解】解：两组对边的长度分别相等，
四边形是平行四边形，故①正确，
向右扭动框架，
的长度变大，故②错误，
平行四边形的底不变，高变小了，
平行四边形的面积变小，故③错误，
平行四边形的四条边不变，
四边形的周长不变，故④正确．
故所有正确的结论是①④．
故答案为：①④
【点睛】本题考查了矩形的性质、平行四边形的判定和性质、平行四边形的周长、面积等知识，解题的关键是熟练应用平行四边形的性质．
18. 如图，在平行四边形中，，于点E，F为的中点，连接，，下列结论：

① ② ③ ④．
其中所有正确结论的序号是______．
【答案】①②③
【解析】
【分析】根据平行四边形的性质，得到，再根据直角三角形斜边中线等于斜边一半，得到， 再利用等边对等角的性质，即可判断①结论；延长、交于点G，易证，得到，再根据直角三角形斜边中线等于斜边一半，即可判断②结论；利用全等三角形的性质和三角形面积，即可证明③结论；过点F作交于点H，则，证明四边形是菱形，得到，根据平行线的性质，得到，再根据等腰三角形三线合一的性质，得到，即可证明④结论．
【详解】解：四边形是平行四边形，
，，，
，
，F为的中点，
，
，
，
，①结论正确；
延长、交于点G，
，
，
，
，，
在和中，
，
，
，
点F是斜边的中线，
，②结论正确；
是的中点，
，
，
，
，③结论正确；
过点F作交于点H，则，
，，
四边形是平行四边形，
，
四边形是菱形，
，
，，
，，
，
，
，
，④结论错误，
综上可知，正确结论的序号是①②③，
故答案为：①②③
【点睛】本题考查了平行四边形的性质，直角三角形斜边中线等于斜边一半，等腰三角形的判定和性质，全等三角形的判定和性质，菱形的判定和性质等知识，灵活运用相关知识解决问题是解题关键．
三、解答题（本大题共9小题，共96分．请在答题卡指定区域内作答，解答时写出必要的文字说明、证明过程或演算步骤）
19. 为了解学生的睡眠情况，某校随机抽取部分学生对他们最近两周的睡眠情况进行调查，得到他们每日平均睡眠时长（单位：）的一组数据，将所得数据分为四组（；；；），并绘制成如下两幅不完整的统计图．

根据以上信息，解答下列问题：
（1）本次一共抽样调查了 名学生，扇形统计图中组所对应的扇形圆心角的度数是 ．
（2）将条形统计图补充完整．
（3）若该校共有900名学生，请估计最近两周约有多少名学生的每日平均睡眠时长大于或等于．
【答案】（1）；
（2）见解析 （3）估计该校有名学生的每日平均睡眠时长大于或等于
【解析】
【分析】（1）由组人数及其所占百分比求出总人数，用乘以D组人数所占比例，即可求解，
（2）根据总人数求出组人数，依此补全图形，
（3）用总人数乘以睡眠时间大于或等于人数所占比例，即可求解，
本题考查了，条形统计图，扇形统计图，解题的关键是：理解两种统计图之间的关系
【小问1详解】
解：本次调查的学生人数为：（名），
D组所对应的扇形圆心角的度数为：，
故答案为：；，
【小问2详解】
解：组人数为：（名），
补全图形如下：
小问3详解】
解：根据题意的：（名），
故答案为：估计该校有名学生的每日平均睡眠时长大于或等于．
20. 某班在义卖活动中设立了一个可以自由转动的转盘，规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是此次活动中的一组统计数据：
（1）完成上述表格：a＝______；b＝______；
（2）请估计当n很大时，频率将会接近______，（精确到0.1）假如你去转动该转盘一次，你获得“书画”奖品的概率约是______；（精确到0.1）
（3）在该转盘中，标有“手工”区域的扇形的圆心角大约是多少度？
【答案】（1）295、0.745
（2）0.6、0.6 （3）在该转盘中，标有“手工”区域的扇形的圆心角大约是144度
【解析】
【分析】（1）根据转动转盘的次数乘以频率求出，由落在“书画”区域的次数除以转动转盘的次数求出；
（2）根据表格确定频率，再根据频率估计概率即可；
（3）用乘以“手工”区域的频率即可得到对应圆心角的度数．
【小问1详解】
，
故答案为：145、0.745；
【小问2详解】
估计当n很大时，频率将会接近0.6，假如转动该转盘一次，获得“书画”奖品的概率约是0.6，
故答案为：0.6、0.6；
【小问3详解】
，
在该转盘中，标有“手工”区域的扇形的圆心角大约是144度．
【点睛】此题考查了利用频率估计概率，频率的计算，扇形部分圆心角的计算，正确理解表格及频率与概率的关系是解题的关键．
21. 如图，、是的对角线所在直线上两点，且，求证：四边形是平行四边形．

【答案】证明见解析
【解析】
【分析】由题意易得，则有，进而问题可求证．
【详解】证明：∵四边形是平行四边形，
∴，，
∴，
∵，∴
∴，
∴，
∴，
，
∴．
∴（内错角相等，两直线平行），
又∵
∴四边形是平行四边形（一组对边平行且相等的四边形是平行四边形）．
【点睛】本题主要考查平行四边形的性质与判定、全等三角形的判定与性质，熟练掌握平行四边形的性质与判定是解题的关键．
22. 已知：如图，在中，，D点是的中点，分别是的角平分线．
（1）请直接写出之间的数量关系： ；
（2）求证：四边形是矩形；
（3）当满足条件 时，四边形是正方形．（直接填空即可）
【答案】（1）
（2）证明见解析 （3）（答案不唯一）
【解析】
【分析】本题主要考查了矩形的判定，正方形的判定，等腰三角形的性质与判定，直角三角形的性质等等：
（1）根据直角三角形斜边上的中线等于斜边的一半即可得到；
（2）由三线合一定理得到，再由有三个角是直角的四边形是矩形即可证明结论；
（3）根据有一组邻边相等的矩形是正方形，只需要满足，而由三线合一定理可得，则只需要满足即可．
【小问1详解】
解：∵在中，，D点是的中点，
∴，
故答案为：；
【小问2详解】
证明：∵，分别是的角平分线，
∴，
又∵，
∴四边形是矩形；
【小问3详解】
解：当满足条件 时，四边形是正方形，理由如下：
∵，分别是的角平分线，
∴，
∵，
∴，
∴矩形是正方形，
故答案为：（答案不唯一）；
23. 图①、图②、图③均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点、、、、均在格点上，只用无刻度的直尺，分别在给定的网格中按下列要求作图，保留作图痕迹．
（1）在图①中，作以点为对称中心的平行四边形．
（2）在图②中，作四边形的边上的高．
（3）在图③中，在四边形的边上找一点，连结，使．
【答案】（1）见解析 （2）见解析
（3）见解析
【解析】
【分析】（1）利用网格特征连接，并延长，即可作以点为对称中心的平行四边形；
（2）取格点，连接交于点，即可作四边形的边上的高；
（3）取格点，，，连接，，，与交于点，连接并延长交于点即可．
【小问1详解】
如图①中，平行四边形即为所求；
【小问2详解】
如图②中，高即为所求；
根据网格与勾股定理得出
∴，
∴，
∵
∴，
∴，
∴，
∴即为所求；
【小问3详解】
如图③中，点即为所求．
如图所示，找到格点，
，，
则是等腰直角三角形，
找到格点，则是矩形，
∴是的中点，
∴垂直平分，
即．
【点睛】本题考查了平行四边形的性质，中心对称的性质，勾股定理与网格问题，矩形的性质，等腰直角三角形的性质，熟练掌握以上知识是解题的关键．
24. 如图，在中，对角线相交于点O，直线l经过点O，且与，分别相交于点E，F，连接．

（1）求证：四边形是平行四边形；
（2）若，求证：四边形是菱形．
【答案】（1）见解析 （2）见解析
【解析】
【分析】（1）证明，则．由对角线互相平分的四边形是平行四边形即可得到结论；
（2）由得到．又由，得到．则．由邻边相等的平行四边形是菱形即可得到结论．
【小问1详解】
证明：四边形为平行四边形，
，，
．
∵，
∴．
．
四边形是平行四边形．
【小问2详解】
，
．
，
．
．
四边形AECF是平行四边形，
四边形AECF是菱形．
【点睛】此题考查了平行四边形的判定和性质、菱形的判定、全等三角形的判定和性质、等角对等边等知识，熟练掌握平行四边形的判定和性质是解题的关键．
25. 在矩形中，，E、F是对角线上的两个动点，分别从A、C同时出发相向而行，速度均为每秒1个单位长度，运动时间为t秒，其中．
（1）若G，H分别是，中点，则四边形一定是怎样的四边形（E、F相遇时除外）？
解： ；（直接填空，不用说理）
（2）在（1）条件下，若四边形为矩形，求t的值；
【答案】（1）四边形是平行四边形
（2）或
【解析】
【分析】本题考查矩形的判定及性质，平行四边形的判定．
（1）由矩形的性质证得，得到，，得到四边形是平行四边形；
（2）连接，则四边形是矩形，．分点E，F相遇前和相遇后两种情况讨论，根据矩形的对角线相等即可解答．
【小问1详解】
∵四边形是矩形，
∴，，
∴，
∵G，H分别是，中点，
∴，，
∴，
∵点E，F的运动速度相同，
∴，
∴，
∴，，
∴，即，
∴，
∴四边形是平行四边形．
故答案为：四边形平行四边形
【小问2详解】
如图1，连接，
图1
∵G，H分别是，中点，
∴，，
∴，
∵，
∵在矩形中，，，
∴四边形是矩形，
∴，
（1）如图1，当四边形是矩形时，
，
∵，
∴，
，
，
；
（2）如图2，当四边形是矩形时，
图2
同理，
，
；
综上所述，四边形为矩形时，或．
26. 如图，在正方形ABCD中，F为BC为边上的定点，E、G分别是AB、CD边上的动点，AF和EG交于点H且AF⊥EG．
（1）求证：AF＝EG；
（2）若AB＝6，BF＝2．
①若BE＝3，求AG的长；
②连结AG、EF，求AG＋EF的最小值．
【答案】（1）见解析；（2）①；②
【解析】
【分析】（1）过点G作GM∥AD交AB于点M，则可得AD=MG，然后证明△GME≌△ABF即可；
（2）①过点G作GM∥AD交AB于点M，连接AG，由（1）可得EM=BF=2，从而可求得AM，在Rt△AMG中由勾股定理即可求得AG的长；
②过点F作FP∥EG，FP=EG，连接AP,则易得GP=EF，当A、G、P三点共线时，AG+EF最小，在Rt△AFP中由勾股定理即可求得AP的长即可．
【详解】（1）过点G作GM∥AD交AB于点M
∵四边形ABCD是正方形
∴∠BAD=∠B=90゜，AB∥CD，AD=AB
∴∠EMG=∠BAD=∠B=90゜
∵AB∥CD，GM∥AD
∴四边形AMGD是平行四边形
∵∠BAD=90゜
∴四边形AMGD是矩形
∴MG=AD
∴MG=AB
∵AF⊥EG
∴∠AEH+∠EAH=90゜
∵∠EAH+∠AFB=90゜
∴∠AEH=∠AFB
在△GME和△ABF中

∴△GME≌△ABF(AAS)
∴AF=EG
（2）①过点G作GM∥AD交AB于点M，连接AG，如图
由（1）知，△GME≌△ABF
∴EM=BF=2
∵AB=6，BE=3
∴AE=AB－BE=3
∴AM=AE－EM=1
在Rt△AMG中，GM=AD=6，由勾股定理得：
②过点F作FP∥EG，FP=EG，连接AP,如图
则四边形EFPG是平行四边形
∴GP=EF
∵AG+GP≥GP
∴当A、G、P三点共线时，AG+EF=AG+GP最小,最小值为线段AP的长
∵AF⊥EG，FP∥EG
∴FP⊥AF
在Rt△ABF中，由勾股定理得
∵AF=EG，EG=FP
∴FP=AF=
在Rt△AFP中，由勾股定理得
所以AG+EF的最小值为．
【点睛】本题考查了正方形的性质，平行四边形的判定与性质，矩形的判定与性质，全等三角形的判定与性质，勾股定理，两点间线段最短等知识，灵活运用这些知识是解决的关键，确定AG+EF最小值是线段AP的长是难点．
27. 如图1，在中，，，点D，E分别在边AB，AC上，，连接BE、P、Q、M分别为DE，BC，BE的中点．
（1）观察猜想：图1中，线段PM与QM的数量关系是______，位置关系是______；
（2）若把图1中的绕点A顺时针旋转到图2的位置，连接PQ，BD，CE，判断的形状，并说明理由；
（3）已知，，将绕点A旋转一周的过程中，请直接写出面积的最大值．
【答案】（1）相等，垂直
（2）是等腰直角三角形，说理过程详见解答
（3）
【解析】
【分析】（1），；，，进一步得出结果；
（2）延长交于交于，证明，从而得出，，进而得出，结合，，，，进一步得出结论；
（3）是等腰直角三角形，当最大时，的面积最大，确定当、、共线时，最大，进一步求得结果．
【小问1详解】
解：，，
，即：，
点是的中点，点是的中点，
，，
，
同理可得：，，
，，
，
，
故答案为：相等，垂直；
【小问2详解】
是等腰直角三角形．
理由如下：如图1所示：
延长交于交于，
，
，即：，
在和中，
，
，
，，
，
，
，
，
是的中位线，
，，
，
同理可得：，，
，，
同理（1）可得：，
是等腰直角三角形；
【小问3详解】
如图2所示：
由（2）知：是等腰直角三角形，且直角边，
当最大时，的面积最大，
，
当、、共线时，最大，
，
．
【点睛】本题考查了等腰直角三角形的判定和性质，全等三角形的判定和性质，三角形中位线定理等知识，解决问题的关键是熟练掌握“手拉手”模型．转动转盘的次数n
100
200
300
400
500
1000
落在“书画”区域的次数m
60
122
180
298
a
604
落在“书画”区域的频率
0.6
061
0.6
b
0.59
0.604