2023-2024学年陕西省西安市碑林区八年级（上）期末数学试卷（含详细答案解析）

这是一份2023-2024学年陕西省西安市碑林区八年级（上）期末数学试卷（含详细答案解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列各数中为无理数的是( )
A. 57B. 3C. −3.1415D. 2022
2.已知点P在第四象限内，到x轴的距离等于3，到y轴的距离等于4，则点P坐标是( )
A. (3,−4)B. (3,4)C. (−4,3)D. (4,−3)
3.如图，两直线a，b被直线c所截，已知a//b，∠1=62∘，则∠2的度数为( )
A. 62∘
B. 108∘
C. 118∘
D. 128∘
4.甲、乙两人相同条件下进行射击练习，每人5次射击成绩的平均数都是8环.方差分别是S甲2=0.4，S乙2=0.8，则两人射击成绩说法正确的是( )
A. 甲成绩比乙稳定B. 乙成绩比甲稳定
C. 甲、乙成绩同样稳定D. 无法比较
5.将一次函数y=−3x−1的图象沿y轴向下平移3个单位长度后，所得图象的函数表达式为( )
A. y=−3(x−3)B. y=−3x+2C. y=−3(x+3)D. y=−3x−4
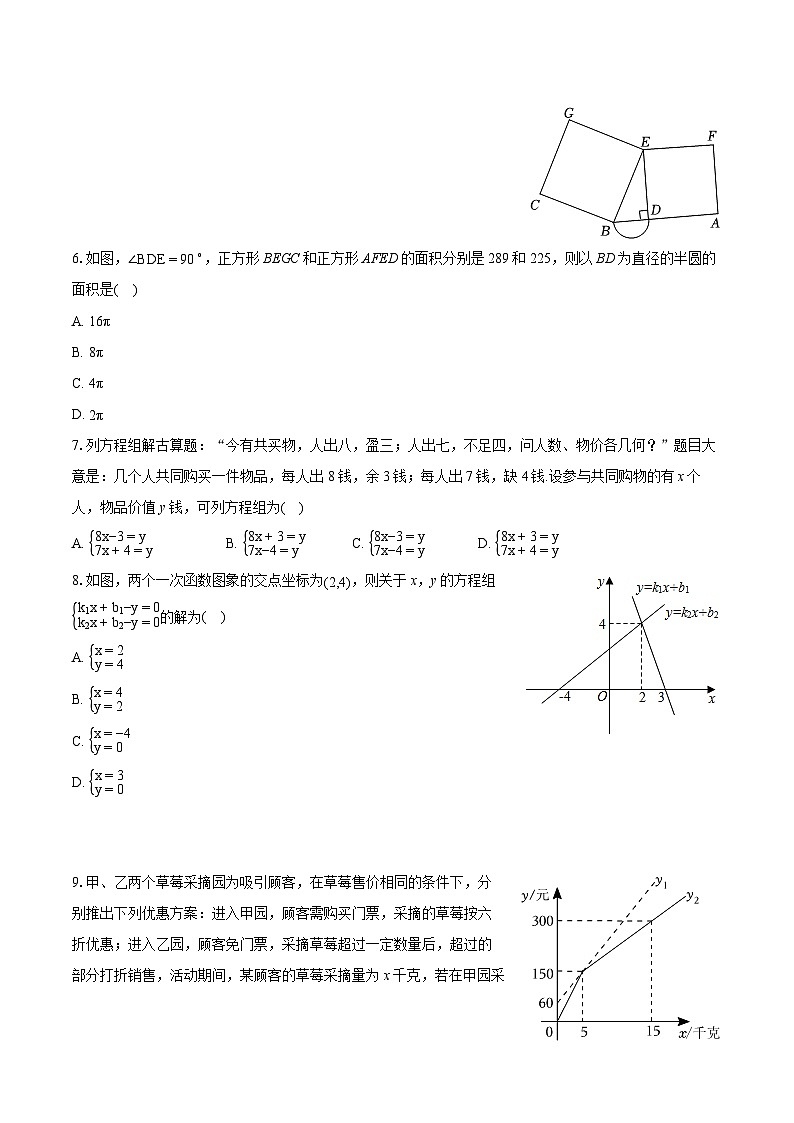
6.如图，∠BDE=90∘，正方形BEGC和正方形AFED的面积分别是289和225，则以BD为直径的半圆的面积是( )
A. 16π
B. 8π
C. 4π
D. 2π
7.列方程组解古算题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”题目大意是：几个人共同购买一件物品，每人出8钱，余3钱；每人出7钱，缺4钱.设参与共同购物的有x个人，物品价值y钱，可列方程组为( )
A. 8x−3=y7x+4=yB. 8x+3=y7x−4=yC. 8x−3=y7x−4=yD. 8x+3=y7x+4=y
8.如图，两个一次函数图象的交点坐标为(2,4)，则关于x，y的方程组k1x+b1−y=0k2x+b2−y=0的解为( )
A. x=2y=4
B. x=4y=2
C. x=−4y=0
D. x=3y=0
9.甲、乙两个草莓采摘园为吸引顾客，在草莓售价相同的条件下，分别推出下列优惠方案：进入甲园，顾客需购买门票，采摘的草莓按六折优惠；进入乙园，顾客免门票，采摘草莓超过一定数量后，超过的部分打折销售，活动期间，某顾客的草莓采摘量为x千克，若在甲园采摘需总费用y1元，在乙园采摘需总费用y2元.y1、y2与x之间的函数图象如图所示，则下列说法中错误的是( )
A. 乙园草莓优惠前的销售价格是30元/千克
B. 甲园的门票费用是60元
C. 乙园超过5千克后，超过部分的价格按五折优惠
D. 顾客用280元在甲园采摘草莓比到乙园采摘草莓更多
二、填空题：本题共6小题，每小题3分，共18分。
10.16的平方根是______.
11.在函数y= x−3中，自变量x的取值范围是______.
12.在平面直角坐标系中，点A的坐标为(2,3)，AB//x轴，且AB=5，则点B的坐标为______.
13.已知直线y=kx经过第二、四象限，则直线y=−x−k不经过第______象限.
14.将△ABC按如图所示翻折，DE为折痕.试写出∠1，∠2和∠C之间的数量关系______.
15.如图，在△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45∘，CD= 2，AD与BE交于点F，连接CF，则AD的长为______.
三、解答题：本题共10小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题5分)
计算： 4−(π+1)0+| 2−1|.
17.(本小题5分)
解方程组：2x−y=7x+3y=−7.
18.(本小题5分)
已知a+b是25的算术平方根，2a−b是−8的立方根，c是 5的整数部分，求a+bc的平方根．
19.(本小题6分)
如图所示的正方形网格中，每个小正方形的边长都为1，△ABC的顶点都在网格线的交点上，点B关于y轴的对称点的坐标为(2,0)，点C关于x轴的对称点的坐标为(−1,−2).
(1)根据上述条件，在网格中建立平面直角坐标系xOy；
(2)画出△ABC分别关于y轴的对称图形△A1B1C1；
(3)写出点A关于x轴的对称点的坐标．
20.(本小题6分)
如图，一高层住宅发生火灾，消防车立即赶到距大厦12米(AC的长)处，升起云梯到火灾窗口，云梯AB长20米，云梯底部距地面3米(AE的长)，问：发生火灾的住户窗口距离地面有多高(BD的长)？
21.(本小题7分)
如图，点E，F，G分别在直线CD，AB，AD上已知∠A=∠D，∠CEB=∠BFG.
(1)FG与BE平行吗？说明理由；
(2)若∠D=30∘，∠BFG=135∘，求∠FGD的度数．
22.(本小题8分)
某快递公司每天下午15：00∼16：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，快件y(件)与时间x(分钟)之间的函数图象如图所示.
(1)求甲仓库揽收快件y(件)与时间x(分钟)之间的函数表达式；
(2)若已知乙仓库用来派发快件y(件)与时间x(分钟)之间的函数表达式是y=−4x+240(0≤x≤60)，则经过多少分钟，甲仓库比乙仓库的快件数量多200件？此时甲仓库的快件数量是多少？
23.(本小题9分)
在学校组织的“学习强国”知识竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分和70分．年级组长张老师将801班和802班的成绩进行整理并绘制成如下的统计图
(1)在本次竞赛中，802班C级的人数有多少？
(2)请你将下面的表格补充完整：
(3)结合以上统计量，请你从不同角度对这次竞赛成绩的结果进行分析(写出两条).
24.(本小题10分)
某山区有23名中、小学生因贫困失学需要捐助．资助一名中学生的学习费用需要a元，一名小学生的学习费用需要b元．某校学生积极捐助，初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表：
(1)求a、b的值；
(2)初三年级学生的捐款解决了其余贫困中小学生的学习费用，求初三年级学生可捐助的贫困中小学生人数．
25.(本小题14分)
如图，直线MN与直线AB，CD分别交于点E，F，∠1与∠2互补.
(1)如图1，求证AB//CD；
(2)如图2，∠BEF与∠EFD的角平分线交于点P，EP的延长线与CD交于点G，点H是MN上一点，且PF//GH，求证：GH⊥EG；
(3)如图3，在(2)的条件下，连接PH，K是GH上一点，使∠PHK=∠HPK，作PQ平分∠EPK，交MN于点Q，∠QPF：∠HPK=3：2，求∠HPF的度数.
答案和解析
1.【答案】B
【解析】解：A.57是分数，不是无理数，不符合题意；
B. 3是无理数，符合题意；
C.−3.1415是分数，不是无理数，不符合题意；
D.2022是整数，不是无理数，不符合题意．
故选：B.
本题考查无理数的定义，根据无理数的定义判断无理数．
本题考查无理数的定义，能够根据无理数的定义判断出无理数是解决本题的关键．
2.【答案】D
【解析】解：∵点P在第四象限内，
∴点P的横坐标大于0，纵坐标小于0，
∵点P到x轴的距离是3，到y轴的距离是4，
∴点P的横坐标是4，纵坐标是−3，即点P的坐标为(4,−3).
故选：D.
先判断出点P的横纵坐标的符号，进而根据到坐标轴的距离判断点的具体坐标．
本题主要考查了点的坐标的几何意义，横坐标的绝对值就是到y轴的距离，纵坐标的绝对值就是到x轴的距离．
3.【答案】C
【解析】解：∵a//b，∠1=62∘，
∴∠3=∠1=62∘，
∴∠2=180∘−∠3=118∘.
故选：C.
根据两直线平行，同位角相等，即可求得∠3的度数，又由邻补角的定义，即可求得∠2的度数．
此题考查了平行线的性质与邻补角的定义．此题比较简单，解题的关键是熟练掌握两直线平行，同位角相等定理的应用．
4.【答案】A
【解析】解：∵每人5次射击成绩的平均数都是8环，方差分别是S甲2=0.4，S乙2=0.8，
∴S甲2