湖北省武汉市黄陂区部分学校2023-2024学年八年级下学期月考数学试题（含解析）

这是一份湖北省武汉市黄陂区部分学校2023-2024学年八年级下学期月考数学试题（含解析），共25页。试卷主要包含了下列运算正确的是，估计的值应在等内容，欢迎下载使用。

一．选择题（共10小题，满分30分，每小题3分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．若二次根式有意义，则的取值范围是（ ）
A．B．C．D．
2．下列根式中，属于最简二次根式的是（ ）
A．B．C．D．
3．下列运算正确的是（ ）
A．B．
C．D．
4．估计的值应在（ ）
A．到之间B．到之间C．到之间D．到之间
5．下列条件中，不能判断为直角三角形的是（ ）
A．B．
C．D．，，
6．已知实数在数轴上的对应点位置如图所示，则化简的结果是（ ）
A．B．C．1D．
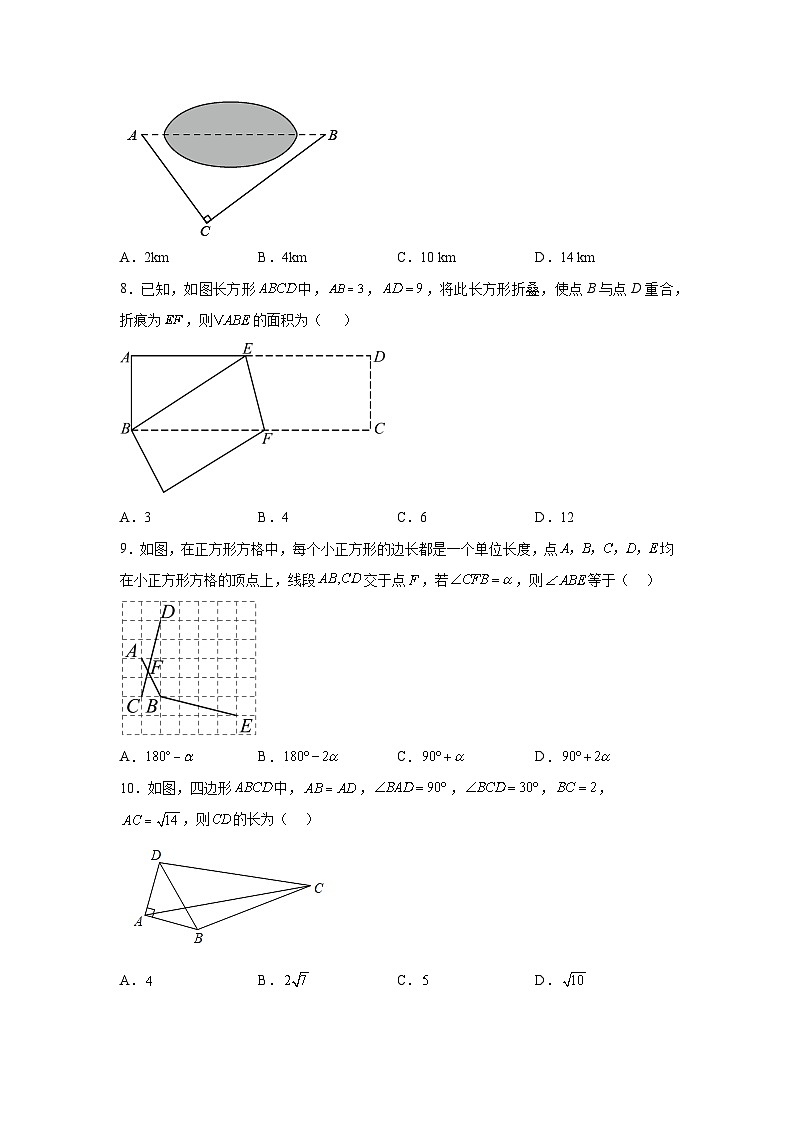
7．如图，原来从A村到B村，需要沿路A→C→B（）绕过两地间的一片湖，在A， B间建好桥后，就可直接从A村到B村．已知，，那么，建好桥后从 A村到B村比原来减少的路程为（ ）
A．2kmB．4kmC．10 kmD．14 km
8．已知，如图长方形中，，，将此长方形折叠，使点B与点D重合，折痕为，则的面积为（ ）

A．3B．4C．6D．12
9．如图，在正方形方格中，每个小正方形的边长都是一个单位长度，点均在小正方形方格的顶点上，线段交于点，若，则等于（ ）

A．B．C．D．
10．如图，四边形中，，，，，，则的长为（ ）
A．B．C．D．
二．填空题（共6小题，满分18分，每小题3分）
11． ．
12．比较下列两个数的大小： ．（用“>”或“<”号填空）
13．如图．从一个大正方形中裁去面积为cm2和cm2的两个小正方形，则留下的阴影部分的面积为 cm2．
14．小明在小区放风筝时，风筝意外挂在了树的顶端，热爱思考的他制定了一个测量树高的方案．如图，在地面A处测得手中剩下的风筝线为4米．后退6米后，在地面B处风筝线恰好用完（点N在点M的正下方，A、B、N在同一条直线上）．已知风筝线总长为8米，则这棵树的高度为 ．
15．勾股数是指能成为直角三角形三条边长的三个正整数，世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》．现有勾股数a，b，c，其中，均小于，，，是大于1的奇数，则 （用含的式子表示）．
16．如图，四边形中，，点是边上一点，是等边三角形，且，则 ．
三．解答题（共8小题，满分72分，解答应写出文字说明、证明过程或演算步棸）
17．计算：
(1)；
(2)．
18．先化简，再求值∶，其中x=，y=4
19．如图四边形中，，求四边形的面积．
20．如图，学校高的教学楼上有一块高的校训宣传牌，为美化环境，对校训牌进行维护．一辆高的工程车在教学楼前点M处，伸长的云梯（云梯最长）刚好接触到的底部点A处．问工程车向教学楼方向行驶多少米，长的云梯刚好接触到的顶部点C处？
21．如图是由小正方形组成的网格，每个小正方形的顶点叫做格点，的三个顶点都是格点，仅用无刻度的直尺在给定网格中按下列要求完成画图，画图过程用虚线表示，画图结果用实线表示．
(1)在图1中按下列步骤完成画图．
①画出的高；
②画的角平分线；
③画点关于的对称点；
(2)如图2，是网格线上一点，过点的线段分别交，于点，，且，画出线段．
22．如图，在中，，点从点A出发，以每秒3个单位长度的速度沿折线运动．设点的运动时间为．

(1)___________；
(2)求斜边上的高线长；
(3)①当在上时，的长为___________，的取值范围是___________；（用含的代数式表示）
②若点在的平分线上，则的值为___________．
23．如图，在△ABC中，∠ACB＝90°,AC＝BC, E为AC边的一点，F为AB边上一点，连接CF,交BE于点D,且∠ACF＝∠CBE, CG平分∠ACB交BD于点G,
(1)如图1,求证: CF＝BG;
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证: PB＝CP＋CF;
(3)如图3，在(2)问的条件下，当∠GAC＝2∠FCH时， 若S△AEG＝3，BG＝6,求AC的长.

24．如图（1），四边形OBCD正方形，O，D两点的坐标分别是（0，0），（0，4）．
(1)直接写出点C的坐标是______；
(2)如图（2），点F为线段BC的中点，点E在线段OB上，若∠EDF＝∠CDF，求点E的坐标；
(3)如图（3），动点E，F分别在边OB，CD上，将正方形OBCD沿直线EF折叠，使点B的对应点M始终落在边OD上（点M不与点O，D重合），点C落在点N处，设OM＝x，四边形BEFC的面积为S，请求出S与x的关系式．
参考答案与解析
1．A
【分析】
根据被开方数为非负数求解即可．
【解答】解：∵二次根式有意义，
∴，
解得：．
故选A．
【点拨】本题考查二次根式有意义的条件．掌握被开方数为非负数是解题关键．
2．C
【分析】本题主要考查最简二次根式的定义，即“被开方数中不含能开得尽方的因数或因式；被开方数的因数是整数，因式是整式”，由此即可求解，掌握最简二次根式的定义，二次根式的性质是解题的关键．
【解答】解：A、，不是最简二次根式，不符合题意；
B、，不是最简二次根式，不符合题意；
C、是最简二次格式，符合题意；
D、是三次根式，不符合题意；
故选：C．
3．D
【分析】本题考查二次根式的计算，根据二次根式的性质可判断选项A；根据二次根式的性质可判断选项B；根据二次根式的除法可判断选项C；根据二次根式的乘法可判断选项D．熟练掌握二次根式的性质及运算法则是解题的关键．
【解答】解：A、，故此选项不符合题意；
B、是最简二次根式，故此选项不符合题意；
C、，故此选项不符合题意；
D、，故此选项符合题意；
故选：D．
4．B
【分析】本题考查了二次根式的混合运算，无理数的估算，先利用二次根式的运算法则将原式化简，再利用夹逼法对无理数进行估算即可求解，掌握夹逼法是解题的关键．
【解答】解：，
∵，
∴，
∴，
即，
故选：．
5．C
【分析】
本题考查了勾股定理逆定理，三角形内角和定理，熟记勾股定理逆定理是解答本题的关键．
根据勾股定理的逆定理，三角形内角和定理分析每个选项，得出正确答案．
【解答】解：根据勾股定理的逆定理，三角形内角和定理，
、，是直角三角形，故不符合题意；
、，，
，即是直角三角形，故不符合题意；
、，
不是直角三角形，故符合题意；
、，
是直角三角形，故不符合题意，
故选：．
6．D
【分析】根据数轴上a点的位置，判断出（a−1）和（a−2）的符号，再根据非负数的性质进行化简．
【解答】解：由图知：1＜a＜2，
∴a−1＞0，a−2＜0，
原式＝a−1-＝a−1＋（a−2）＝2a−3．
故选D．
【点拨】此题主要考查了二次根式的性质与化简，正确得出a−1＞0，a−2＜0是解题关键．
7．B
【分析】直接利用勾股定理得出的长，进而得出答案．
【解答】解：由题意可得：
则打通隧道后从A村到B村比原来减少的路程为：（km）．
故选：B．
【点拨】此题主要考查了勾股定理的应用，正确得出的长是解题关键．
8．C
【分析】本题考查了折叠问题，三角形的面积，勾股定理等，熟练掌握折叠的性质是解题的关键．
首先根据折叠的性质得到，设，则，然后在中利用勾股定理求出，然后利用三角形面积公式求解即可．
【解答】解：∵长方形折叠，使点B与点D重合，
∴，
设，则，
在中，，
∴，
解得：，
∴的面积为．
故选：C．
9．C
【分析】
根据三角形外角的性质及平行线的性质可进行求解．
【解答】解：如图，

由图可知：，，
∴，
∴，
∵，
∴，
∵，
∴，
∴；
故选C．
【点拨】本题主要考查全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．
10．A
【分析】把绕点逆时针旋转得到，连接，作于，则，易得△ACE为等腰直角三角形，，结合旋转的性质求得，，，在中，，然后利用含角的直角三角形性质及勾股定理求解即可．
【解答】解：如图，把绕点逆时针旋转度，得到，连接，过点作延长线于点，

根据旋转可知：，，，，
∴，
∴，
根据四边形的内角和，
，
，，
，
，
，
，
，
在中，，
，，
在中，，
．
故选：A．
【点拨】本题考查图形的旋转，四边形的内角和，直角三角形的性质和勾股定理．解题的关键是把绕点逆时针旋转得到，证明出．
11．
【分析】
本题主要考查了二次根式的加减运算，解题的关键是先根据二次根式的性质进行化简，然后再根据二次根式加减运算法则进行计算即可．
【解答】解：．
故答案为：．
12．
【分析】
根据二次根式比较大小的方法求解即可．
【解答】解：，，
∵，
∴，
故答案为：．
【点拨】本题主要考查了比较二次根式的大小，正确化简两个二次根式是解题的关键．
13．24
【分析】通过两个小正方形的面积，分别求出正方形的边长，则可求最大的正方形的边长为5cm，再用大正方形面积减去两个小正方形面积求解即可．
【解答】解：∵小正方形的面积8cm2，
∴小正方形的边长为=2(cm)，
∵大正方形的面积18cm2，
∴大正方形的边长为=3(cm)，
∵最外边的大正方形的边长为2+3=5(cm)，
∴S=（5）2=50(cm2)，
∴S阴影=50-8-18=24(cm2)，
故答案为：24．
【点拨】本题考查二次根式的应用，熟练掌握二次根式的化简运算，结合图形求面积是解题的关键．
14．米##
【分析】此题考查了勾股定理的应用．根据勾股定理求解即可．
【解答】解：根据题意得，米，（米），米，
∴，，
∴，，
∴，
∴（负值已舍去），
故答案为：米．
15．
【分析】
根据直角三角形的性质，直角边小于斜边得到，为直角边，为斜边，根据勾股定理即可得到的值．
【解答】解：由于现有勾股数a，b，c，其中，均小于，
，为直角边，为斜边，
，
，
得到，
，
，
是大于1的奇数，
．
故答案为：．
【点拨】本题考查勾股定理的应用，分清楚，为直角边，为斜边是解题的关键．
16．
【分析】作，交的延长线于点M，交的延长线于点，根据已知可得，再利用等边三角形的性质可得，，从而可得，然后证明，利用全等三角形的性质可得，，再根据已知设，，从而在和中，利用锐角三角函数的定义进行计算求出，，，的长，从而求出，的长，进行计算即可解答．
【解答】解：作，交的延长线于点M，交的延长线于点，如图所示：
，
，
，，
，
是等边三角形，
，，
，
，
，
，
，，
，
设，，
在中，，，
，
在中，，，
，
，，
，
，
故答案为：．
【点拨】本题考查了全等三角形的判定与性质，解直角三角形，等边三角形的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
17．(1)
(2)
【分析】此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．
（1）直接化简二次根式，再合并得出答案；
（2）先利用平方差公式进行乘法运算，同时进行除法运算后化简，进而得出答案；
【解答】（1）解：
；
（2）解：
．
18．，
【分析】先确定，再利用二次根式的性质化简，然后计算二次根式的加减法，最后将的值代入计算即可得．
【解答】解：由题意得：，
，
则
，
将代入得：原式．
【点拨】本题考查了二次根式的化简求值，熟练掌握运算法则是解题关键．
19．36
【分析】
本题主要考查了勾股定理及其逆定理．根据勾股定理可求得的长，再根据勾股定理逆定理可求得为直角三角形，，即可求得结果．
【解答】
解：∵，
∴为直角三角形，
又∵，
∴根据勾股定理得： ，
又∵，
∴，
∴，
∴为直角三角形，，
∴．
即四边形的面积是36．
20．工程车再向教学楼方向行驶5米．
【分析】
过点作交于点，在根据勾股定理求出的长，设，则，在中根据勾股定理列方程求出x即可．
本题主要考查了根据勾股定理解决实际问题，熟练掌握勾股定理是解题的关键．
【解答】
过点作交于点，
由题意得，
在中，
，
设，则，
在中，
，
∴，
解得，
工程车再向教学楼方向行驶5米，云梯刚好接触到的顶部点处．
21．(1)①见解析；②见解析；③见解析
(2)见解析
【分析】（1）①取格点，连接交于点，此时是的高；
②取格点，与的交点即为点，连接；
③分别画，关于的对称线段和，和的交点即为点关于的对称点；
(2)连接并延长交网格线于点，则，连接并延长交网格线于点，则，连接交于点，延长交于点，则线段即为所画的线段．
【解答】（1）解：（1）①如图所示,CD为所求；
②如图所示,AE为所求；
③如图所示, 为所求；
（2）如图所示, 线段为所求．
【点拨】此题考查作图一应用与设计作图,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考常考题型．
22．(1)8
(2)斜边上的高线长为
(3)①；；②
【分析】（1）利用勾股定理求解；
（2）过点作于点，利用面积法求解；
（3）①根据点P的运动路径及速度可解；②过点作于，利用角平分线的性质可知，再证，推出，最后利用勾股定理解即可；
【解答】（1）解：在中，，，，
，
故答案为：8；
（2）解：如图所示，过点作于点，

，
即，
∴斜边上的高线长为；
（3）解：①点P从点A出发，以每秒3个单位长度的速度沿折线运动，，当在上时，
，
，即，
，
②点在的角平分线上时，过点作于，如图所示，

∵平分，，，
∴，
又∵，
∴，
∴，则，
由（2）知，
∴，
∴，
在中，，
即，
解方程得，，
∴点在的角平分线上时，．
故答案为：①；；②；
【点拨】本题考查三角形上的动点问题，涉及勾股定理，等腰三角形的性质，角平分线的性质，全等三角形的判定等知识点，熟练掌握上述定理、性质是解题的关键．
23．（1）见解答；（2）见解答；（3）3+3
【分析】（1）根据ASA证明△BCG≌△CAF，则CF=BG；
（2）先证明△ACG≌△BCG，得∠CAG=∠CBE，再证明∠PCG=∠PGC，即可得出结论；
（3）作△AEG的高线EM，根据角的大小关系得出∠CAG=30°，根据面积求出EM的长，利用30°角的三角函数值依次求AE、EG、BE的长，所以CE=3+，根据线段的和得出AC的长．
【解答】解：：（1）∵∠ACB=90°，AC=BC，
∴∠A=45°，
∵CG平分∠ACB，
∴∠ACG=∠BCG=45°，
∴∠A=∠BCG，
在△BCG和△CAF中，
，
∴△BCG≌△CAF（ASA），
∴CF=BG；
（2）∵PC∥AG，
∴∠PCA=∠CAG，
∵AC=BC，∠ACG=∠BCG，CG=CG，
∴△ACG≌△BCG，
∴∠CAG=∠CBE，
∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°，
∠PGC=∠GCB+∠CBE=∠CBE+45°，
∴∠PCG=∠PGC，
∴PC=PG，
∵PB=BG+PG，BG=CF，
∴PB=CF+CP；
(3)过E作EM⊥AG，交AG于M，

∵S△AEG=AG•EM=3 ，
由（2）得：△ACG≌△BCG，
∴BG=AG=6，
∴×6×EM=3，
EM=，
设∠FCH=x°，则∠GAC=2x°，
∴∠ACF=∠EBC=∠GAC=2x°，
∵∠ACH=45°，
∴2x+x=45，
x=15，
∴∠ACF=∠GAC=30°，
在Rt△AEM中，AE=2EM=2，

∴M是AG的中点，
∴AE=EG=2，
∴BE=BG+EG=6+2，
在Rt△ECB中，∠EBC=30°，
∴CE=BE=3+，
∴AC=AE+EC=2+3+=3+3．
【点拨】本题考查了全等三角形的性质和判定及等腰直角三角形的性质，证明两线段相等时，一般都是证明两线段所在的三角形全等．
24．(1)（4，4）；
(2)E（3，0）；
(3)S=x2-2x+8（0＜x＜4）．
【分析】（1）根据正方形的性质和D点的坐标得出C点坐标即可；
（2）过点F作FG⊥DE于点G，连接EF，证△DGF≌△DCF（AAS），得GF=BF=2，证Rt△EFG≌Rt△EFB（HL），得GE=BE，根据勾股定理求出OE即可确定E点坐标；
（3）设ME=BE=m，CF=n，且m＞0，n＞0，分别用含有x的代数式表示出m和n，再根据三角形面积公式得出S和x的关系式即可．
【解答】（1）∵四边形OBCD是正方形，O（0，0），D（0，4），
∴OB=BC=CD=OD=4，BC⊥x轴，
∴C（4，4），
故答案为：（4，4）；
（2）如下图，过点F作FG⊥DE于点G，连接EF，
∵四边形OBCD是正方形，O（0，0），D（0，4），
∴OB=BC=CD=OD=4，∠C=∠OBC=∠BOD=90°，
∵FG⊥DE，
∴∠DGF=∠C=90°，
在△DGF和△DCF中，
∴△DGF≌△DCF（AAS），
∴GD=CD=4，GF=CF，
∵点F为线段BC的中点，
∴BF=CF=BC=×4=2，
∴GF=BF=2，
在Rt△EFG和Rt△EFB中，
∴Rt△EFG≌Rt△EFB（HL），
∴GE=BE，
设OE=a（a＞0），则GE=BE=OB-OE=4-a，
∴DE=GD+GE=4+4-a=8-a，
在Rt△DOE中，根据勾股定理得，OE2+OD2=DE2，
即a2+42=（8-a）2，
解得a=3，
∴OE=3，
∵点E在x轴的正半轴上，
∴E（3，0）；
（3）如下图，分别连接BM、MF、BF，
∵EF是折痕，
∴EF垂直平分BM，
∴ME=BE，MF=BF，
设ME=BE=m，CF=n，且m＞0，n＞0，
则OE=OB-BE=4-m，DF=CD-CF=4-n，
∵OM=x，点B的对应点M始终落在边OD上（M不与点O，D重合），
∴DM=OD-OM=4-x（0＜x＜4），
在Rt△DMF中，根据勾股定理得，OM2+OE2=ME2，
即x2+（4-m）2=m2，
解得m=，
在Rt△DMF和Rt△CBF中，BF2=BC2+CF2，
∵MF=BF，
∴DM2+DF2=BC2+CF2，
∴（4-x）2+（4-n）2=42+n2，
解得n=，
即CF=n=，
∵S=S四边形BEFC=（CF+BE）•BC，
∴S==，
即S和x的关系式为：S=（0＜x＜4）．
【点拨】本题主要考查四边形的综合题，熟练掌握正方形的性质，折叠的性质，全等三角形的判定和性质等知识是解题的关键．