河北省石家庄市第二十八中学2022—2023学年下学期七年级期中数学试卷

这是一份河北省石家庄市第二十八中学2022—2023学年下学期七年级期中数学试卷，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下面的各组图案中，不能由其中一个经过平移后得到另一个的是（ ）
A．B．
C．D．
2．（3分）在下列方程组中，不是二元一次方程组的是（ ）
A．B．
C．D．
3．（3分）下列命题中，属于真命题的是（ ）
A．如果a＝﹣2，那么a2＝4
B．如果|a|＝a，那么a＞0
C．如果两个角相等，那么这两个角都为90°
D．同位角相等
4．（3分）下列运算中，计算结果正确的是（ ）
A．a4•a＝a4B．a6÷a3＝a2
C．（a3）2＝a5D．（ab）3＝a3b3
5．（3分）现用三根木棒搭一个三角形，其中两根木棒的长分别是2cm和6cm，那么第三根的长不可能是（ ）
A．5cmB．6cmC．7cmD．8cm
6．（3分）下列多项式的乘法中可用平方差公式计算的是（ ）
A．（1+x）（x+1）B．（a+b）（b﹣a）
C．（﹣a+b）（a﹣b）D．（x2﹣y）（y2+x）
7．（3分）代入法解方程组时，代入正确的是（ ）
A．x﹣4x+1＝4B．x﹣2（2x﹣1）＝4
C．x﹣4x﹣1＝4D．x﹣4x﹣2＝4
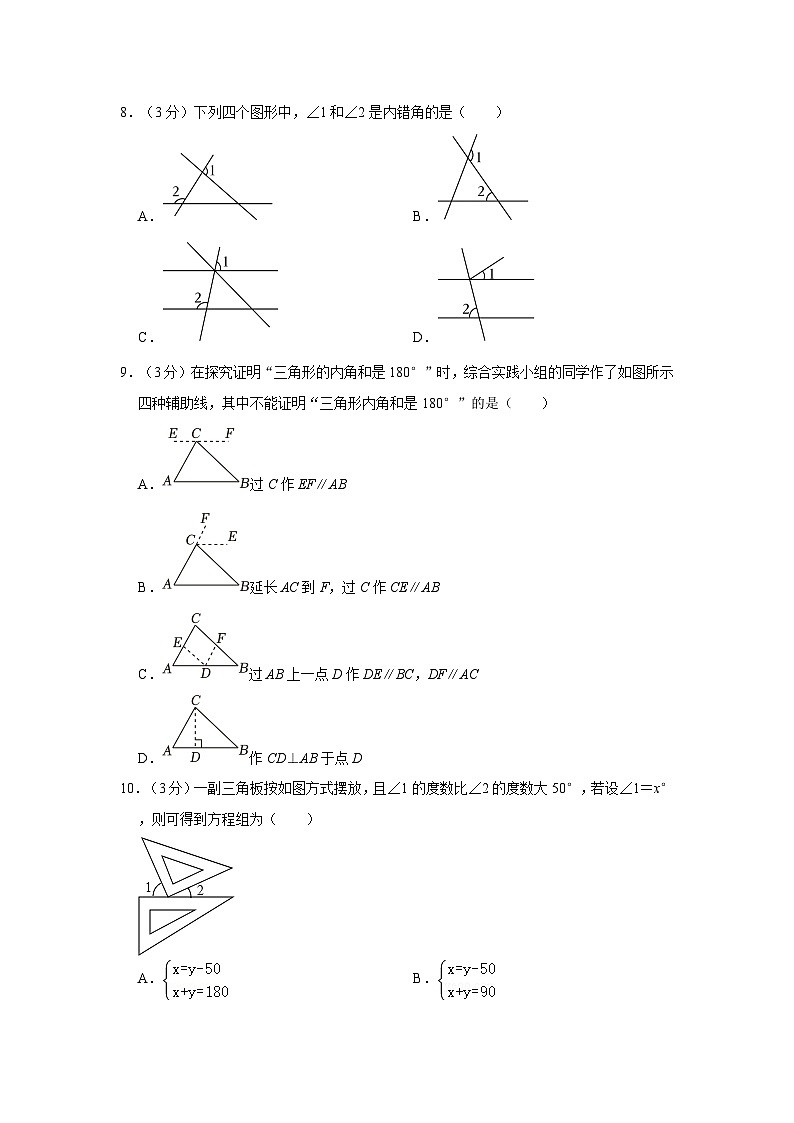
8．（3分）下列四个图形中，∠1和∠2是内错角的是（ ）
A．B．
C．D．
9．（3分）在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如图所示四种辅助线，其中不能证明“三角形内角和是180°”的是（ ）
A．过C作EF∥AB
B．延长AC到F，过C作CE∥AB
C．过AB上一点D作DE∥BC，DF∥AC
D．作CD⊥AB于点D
10．（3分）一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1＝x°，则可得到方程组为（ ）
A．B．
C．D．
11．（3分）如图，下列条件①∠1＝∠2；②∠BAD＝∠BCD；④∠BAD+∠ADC＝180°．其中能判定AB∥CD的有（ ）
A．1个B．2个C．3个D．4个
12．（3分）若（x﹣3）（x2+ax+b）的积中不含x的二次项和一次项，则a和b的值（ ）
A．a＝0；b＝2B．a＝3；b＝9C．a＝﹣1；b＝2D．a＝2；b＝4
13．（3分）已知一个甲种病毒的质量为7×10﹣11千克，一个乙种病毒的质量为1.8×10﹣12千克．若一个甲种病毒和一个乙种病毒的质量之和为m千克，则m用科学记数法可以表示为（ ）
A．8.8×10﹣11B．7.18×10﹣11
C．8.8×10﹣12D．7.18×10﹣12
14．（3分）要得知作业纸上两相交直线AB，CD所夹锐角的大小，发现其交点不在作业纸内（如图1和图2）：
对于方案Ⅰ、Ⅱ，说法正确的是（ ）
A．Ⅰ可行、Ⅱ不可行B．Ⅰ不可行、Ⅱ可行
C．Ⅰ、Ⅱ都可行D．Ⅰ、Ⅱ都不可行
15．（3分）已知有若干片相同的拼图，其形状如图1所示．当4片拼图紧密拼成一列时，总长度为23cm；当10片拼图紧密拼成一列时，总长度为56cm，则图1中的拼图长度为（ ）
A．5.5cmB．5.6cmC．5.75cmD．6.5cm
16．（3分）我国南宋数学家杨辉所著的《详解九章算术》一书中，利用如图所示的“三角形”解释二项式（a+b）n的展开式的各项系数，此“三角形”称为“杨辉三角”．如（a+b）3＝a3+3a2b+3ab2+b2其展开式的系数从左起依次是1，3，3，1，请根据“杨辉三角”计算（a+b）8的展开式中从左起第四项的系数为（ ）
A．84B．56C．35D．28
二、填空题
17．（3分）若2x﹣1＝42，则x＝ ．
18．（3分）如图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠E保持不变．为了舒适，需调整∠D的大小，则图中∠D应 （填“增加”或“减少”） 度．
19．（3分）我们定义：三角形＝ab•ac，五角星＝z•（xm•yn）；
（1）＝ ；
（2）若＝4，则＝ ．
三、解答题
20．计算：
（1）解方程组：；
（2）；
（3）20222﹣2023×2021；
（4）（x﹣1）（x+1）（x2+1）．
21．已知多项式A＝（x+2）2+x（x﹣2）﹣（x+3）（x﹣3）．
（1）化简多项式A时，小明的结果与其他同学的不同，请你检查小明同学的解题过程．
在标出①②③的几项中，出现错误的是 ．请写出正确的解答过程；
（2）小亮说：“只要给出x2+2x+1的合理的值，即可求出多项式A的值”．小明给出x2+2x+1的值为4，请你求出此时A的值．
22．已知：如图，∠BEC＝∠B+∠C，求证：AB∥CD．
证明：延长BE交 于点F，
则∠BEC＝ +∠C，
又∵∠BEC＝∠B+∠C，
∴∠B＝ ，
∴AB∥CD（ 相等，两直线平行）．
23．如图所示的格线彼此平行．小明在格线中作已知角，探究角的两边与格线形成的锐角所满足的数量关系．他先作出∠AOB＝60°，
（1）①如图1，点O在一条格线上，当∠1＝20°时 °；
②如图2，点O在两条格线之间，用等式表示∠1与∠2之间的数量关系；
（2）在图3中，小明作射线OC，使得∠COB＝45°．记OA与图中一条格线形成的锐角为α，请直接用等式表示α与B之间的数量关系．
24．根据图中给出的信息，解答下列问题：
（1）放入一个小球水面升高 cm，放入一个大球水面升高 cm；
（2）如果要使水面上升到55cm，应放入大球、小球各多少个？
25．两个边长分别为a和b的正方形按图1放置，其未叠合部分（阴影）面积记作S1，若再在图1中大正方形的右下角摆放一个边长为b的小正方形，如图2所示，两个小正方形叠合部分（阴影）2．
（1）用含a，b的代数式分别表示S1，S2；
（2）若a+b＝15，ab＝5，求S1+S2的值．
26．将一个直角三角形纸板ABC放置在锐角△PMN上，使该直角三角形纸板的两条直角边AB，AC分别经过点M
【发现】
（1）如图1，若点A在△PMN内，当∠P＝40°时 ；
（2）如图2，若点A在△PMN内，当∠P＝60°时 ；
【探究】
若点A在△PMN内，请你判断∠PMA，∠PNA和∠P之间满足怎样的数量关系；
【应用】
如图3，点A在△PMN内，过点P作直线EF∥AB，求∠NPE的度数；
【拓展】
如图4，当点A在△PMN外，请直接写出∠PMA ．
参考答案与试题解析
一、选择题
1．（3分）下面的各组图案中，不能由其中一个经过平移后得到另一个的是（ ）
A．B．
C．D．
【解答】解：A、能由其中一个经平移后得到另一个；
B、能由其中一个经平移后得到另一个；
C、不能由其中一个经平移后得到另一个；
D、能由其中一个经平移后得到另一个；
故选：C．
2．（3分）在下列方程组中，不是二元一次方程组的是（ ）
A．B．
C．D．
【解答】解：选项C中的第二个方程是分式方程，所以它不是二元一次方程组．
故选：C．
3．（3分）下列命题中，属于真命题的是（ ）
A．如果a＝﹣2，那么a2＝4
B．如果|a|＝a，那么a＞0
C．如果两个角相等，那么这两个角都为90°
D．同位角相等
【解答】解：A、如果a＝﹣22＝6，正确，符合题意；
B、如果|a|＝a，故错误，不符合题意；
C、两个角相等不一定都等于90°，是假命题；
D、两直线平行，故错误，不符合题意．
故选：A．
4．（3分）下列运算中，计算结果正确的是（ ）
A．a4•a＝a4B．a6÷a3＝a2
C．（a3）2＝a5D．（ab）3＝a3b3
【解答】解：A、a4•a＝a5，故本选项不合题意；
B、a2÷a3＝a3，故本选项不合题意；
C、（a4）2＝a6，故本选项不合题意；
D、（ab）2＝a3b3，故本选项符合题意；
故选：D．
5．（3分）现用三根木棒搭一个三角形，其中两根木棒的长分别是2cm和6cm，那么第三根的长不可能是（ ）
A．5cmB．6cmC．7cmD．8cm
【解答】解：设第三根的长是x cm，
∴6﹣2＜x＜7+6，
∴4＜x＜3，
∴第三根的长不可能是8cm．
故选：D．
6．（3分）下列多项式的乘法中可用平方差公式计算的是（ ）
A．（1+x）（x+1）B．（a+b）（b﹣a）
C．（﹣a+b）（a﹣b）D．（x2﹣y）（y2+x）
【解答】解：A、两项相同；
B、有一项相同．符合平方差公式的特征；
C、两项都互为相反数；
D、两项都不相同．
故选：B．
7．（3分）代入法解方程组时，代入正确的是（ ）
A．x﹣4x+1＝4B．x﹣2（2x﹣1）＝4
C．x﹣4x﹣1＝4D．x﹣4x﹣2＝4
【解答】解：用代入法解方程组时，代入正确的是x﹣2（5x﹣1）＝4，
故选：B．
8．（3分）下列四个图形中，∠1和∠2是内错角的是（ ）
A．B．
C．D．
【解答】解：A．∠1与∠2不是内错角；
B．∠2与∠2是内错角；
C．∠1与∠5不是内错角；
D．∠1和∠2不是内错角；
故选：B．
9．（3分）在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如图所示四种辅助线，其中不能证明“三角形内角和是180°”的是（ ）
A．过C作EF∥AB
B．延长AC到F，过C作CE∥AB
C．过AB上一点D作DE∥BC，DF∥AC
D．作CD⊥AB于点D
【解答】解：A．由EF∥AB，∠FCB＝∠B，得∠A+∠ACB+∠B＝180°．
B．由CE∥AB，∠B＝∠BCE，得∠∠A+∠B+∠ACB＝180°．
C．由ED∥BC，∠A＝∠FDB，得∠EDA＝∠B，那么∠C＝∠EDF，得∠B+∠A+∠C＝180°．
D．由CD⊥AB于D，无法证得三角形内角和是180°．
故选：D．
10．（3分）一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1＝x°，则可得到方程组为（ ）
A．B．
C．D．
【解答】解：由图可知：∠1+∠2＝90°，
又∵∠2＝∠2+50°，
∴联立方程组可得
故选：C．
11．（3分）如图，下列条件①∠1＝∠2；②∠BAD＝∠BCD；④∠BAD+∠ADC＝180°．其中能判定AB∥CD的有（ ）
A．1个B．2个C．3个D．4个
【解答】解：①由∠1＝∠2，得到AD∥BC；②由∠BAD＝∠BCD，本选项不合题意，得到AD∥BC；④由∠BAD+∠ADC＝180°，本选项合题意，
则符合题意的只有4个．
故选：A．
12．（3分）若（x﹣3）（x2+ax+b）的积中不含x的二次项和一次项，则a和b的值（ ）
A．a＝0；b＝2B．a＝3；b＝9C．a＝﹣1；b＝2D．a＝2；b＝4
【解答】解：原式＝x3+ax2+bx﹣3x2﹣3ax﹣4b
＝x3+ax2﹣6x2﹣3ax+bx﹣5b
＝x3+（a﹣3）x5﹣（3a﹣b）x﹣3b
由题意可知：a﹣8＝0，3a﹣b＝6，
∴a＝3，b＝9
故选：B．
13．（3分）已知一个甲种病毒的质量为7×10﹣11千克，一个乙种病毒的质量为1.8×10﹣12千克．若一个甲种病毒和一个乙种病毒的质量之和为m千克，则m用科学记数法可以表示为（ ）
A．8.8×10﹣11B．7.18×10﹣11
C．8.8×10﹣12D．7.18×10﹣12
【解答】解：7×10﹣11+1.3×10﹣12＝7.18×10﹣11，
∴m＝7.18×10﹣11，
故选：B．
14．（3分）要得知作业纸上两相交直线AB，CD所夹锐角的大小，发现其交点不在作业纸内（如图1和图2）：
对于方案Ⅰ、Ⅱ，说法正确的是（ ）
A．Ⅰ可行、Ⅱ不可行B．Ⅰ不可行、Ⅱ可行
C．Ⅰ、Ⅱ都可行D．Ⅰ、Ⅱ都不可行
【解答】解：方案Ⅰ，∵∠HEN＝∠CFG，
∴MN∥CD，
根据两直线平行，内错角相等可知，CD所夹锐角与∠AEM相等，
故方案Ⅰ可行，
方案Ⅱ，根据三角形内角和定理可知，CD所夹锐角与180°﹣∠AEH﹣∠CFG相等，
故方案Ⅱ可行，
故选：C．
15．（3分）已知有若干片相同的拼图，其形状如图1所示．当4片拼图紧密拼成一列时，总长度为23cm；当10片拼图紧密拼成一列时，总长度为56cm，则图1中的拼图长度为（ ）
A．5.5cmB．5.6cmC．5.75cmD．6.5cm
【解答】解：设图1中一个拼图中去掉半圆的宽度为x cm，半圆的半径长为y cm，
由题意得：，
解得：，
则x+y＝3.5+1＝5.5，
即图1中的拼图长度为8.5cm，
故选：D．
16．（3分）我国南宋数学家杨辉所著的《详解九章算术》一书中，利用如图所示的“三角形”解释二项式（a+b）n的展开式的各项系数，此“三角形”称为“杨辉三角”．如（a+b）3＝a3+3a2b+3ab2+b2其展开式的系数从左起依次是1，3，3，1，请根据“杨辉三角”计算（a+b）8的展开式中从左起第四项的系数为（ ）
A．84B．56C．35D．28
【解答】解：根据“杨辉三角”得：
（a+b）7的展开式中的系数分别为1，7，21，35，7，1，
（a+b）8的展开式中的系数分别为1，8，28，70，28，5，1，
则（a+b）8的展开式中从左起第四项的系数为56，
故选：B．
二、填空题
17．（3分）若2x﹣1＝42，则x＝ 5 ．
【解答】解：∵2x﹣1＝32，
∴2x﹣5＝（22）7＝24，
∴x﹣6＝4，
∴x＝5，
故答案为：3．
18．（3分）如图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠E保持不变．为了舒适，需调整∠D的大小，则图中∠D应 减少 （填“增加”或“减少”） 10 度．
【解答】解：连接CF，并延长至点M．
在△ABC中，∠A＝50°，
∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣50°﹣60°＝70°，
∴∠DCE＝∠ACB＝70°．
∵∠DFM＝∠DCF+∠D，∠EFM＝∠ECF+∠E，
∴∠EFD＝∠DCF+∠ECF+∠D+∠E＝∠DCE+∠D+∠E，
即110°＝70°+∠D+30°，
∴∠D＝10°，
∴20°﹣10°＝10°，
∴图中∠D应减少（填“增加”或“减少”）10度．
故答案为：减少；10．
19．（3分）我们定义：三角形＝ab•ac，五角星＝z•（xm•yn）；
（1）＝ 27 ；
（2）若＝4，则＝ 32 ．
【解答】解：（1）由题意得：＝31×22＝38＝27，
故答案为：27；
（2）∵＝4，
∴3x•32y＝4，
∴3x+2y＝4，
∴＝4×（9x•81y）
＝2×[（72）x•（35）y]
＝2×（36x•34y）
＝3×32x+2y
＝2×38（x+2y）
＝2×[2（x+2y）]2
＝7×42
＝8×16
＝32，
故答案为：32．
三、解答题
20．计算：
（1）解方程组：；
（2）；
（3）20222﹣2023×2021；
（4）（x﹣1）（x+1）（x2+1）．
【解答】解：（1），
①﹣②×3，得11y＝22，
解得y＝6，
把y＝2代入②，得
x﹣2×8＝﹣3，
解得x＝3，
∴该方程组的解为；
（2）；
＝1﹣+9﹣5
＝5；
（3）20222﹣2023×2021
＝20222﹣（2022+5）×（2022﹣1）
＝20222﹣20222+1
＝1；
（4）（x﹣8）（x+1）（x2+5）
＝（x2﹣1）（x8+1）
＝x4﹣6．
21．已知多项式A＝（x+2）2+x（x﹣2）﹣（x+3）（x﹣3）．
（1）化简多项式A时，小明的结果与其他同学的不同，请你检查小明同学的解题过程．
在标出①②③的几项中，出现错误的是 ①③ ．请写出正确的解答过程；
（2）小亮说：“只要给出x2+2x+1的合理的值，即可求出多项式A的值”．小明给出x2+2x+1的值为4，请你求出此时A的值．
【解答】解：（1）A＝（x+2）2+x（x﹣2）﹣（x+3）（x﹣3）
＝x6+4x+4+x8﹣2x﹣x2+5
＝x2+2x+13，
故出现错误的是：①③；
故答案为：①③；
（2）∵x2+2x+1＝2，
∴x2+2x＝2，
则A＝x2+2x+13＝6+13＝16．
22．已知：如图，∠BEC＝∠B+∠C，求证：AB∥CD．
证明：延长BE交 CD 于点F，
则∠BEC＝ ∠EFC +∠C，
又∵∠BEC＝∠B+∠C，
∴∠B＝ ∠EFC ，
∴AB∥CD（ 内错角 相等，两直线平行）．
【解答】证明：延长BE交CD于点F，
则∠BEC＝∠EFC+∠C，
又∵∠BEC＝∠B+∠C，
∴∠B＝∠EFC，
∴AB∥CD（内错角相等，两直线平行）．
故答案为：CD、∠EFC，内错角．
23．如图所示的格线彼此平行．小明在格线中作已知角，探究角的两边与格线形成的锐角所满足的数量关系．他先作出∠AOB＝60°，
（1）①如图1，点O在一条格线上，当∠1＝20°时 40 °；
②如图2，点O在两条格线之间，用等式表示∠1与∠2之间的数量关系；
（2）在图3中，小明作射线OC，使得∠COB＝45°．记OA与图中一条格线形成的锐角为α，请直接用等式表示α与B之间的数量关系．
【解答】解：（1）如图：
①如图1：∵格线都互相平行，
∴∠2＝∠7，∠1＝∠3＝20°，
∵∠AOB＝60°，
∴∠3＝∠AOB﹣∠3＝40°，
∴∠2＝∠3＝40°，
故答案为：40°；
②∠1+∠2＝60°，
证明：如图7：作OP平行于格线，
∵格线都互相平行，
∴∠1＝∠AOP，∠2＝∠BOP，
∵∠AOB＝∠AOP+∠BOP＝60°
∴∠5+∠2＝60°；
（2）α+β＝105°或α﹣β＝15°，
理由：分两种情况：
当射线OC在∠AOB的内部，如图：
∵∠COB＝45°，∠AOB＝60°，
∴∠AOC＝∠AOB﹣∠COB＝15°，
∴∠AEF是△OEF的一个外角，
∴∠AEF＝∠AOC+∠EFO，
∵格线都互相平行，
∴∠EFO＝β，
∴α＝15°+β，
∴α﹣β＝15°；
当射线OC在∠AOB的外部，如图：
∵∠COB＝45°，∠AOB＝60°，
∴∠AOC＝∠AOB+∠COB＝105°，
∵∠AOC是△OMN的一个外角，
∴∠AOC＝∠OMB+∠ONM，
∵格线都互相平行，
∴∠OMB＝α，
∵∠ONM＝β，
∴α+β＝105°，
综上所述：α+β＝105°或α﹣β＝15°．
24．根据图中给出的信息，解答下列问题：
（1）放入一个小球水面升高 2 cm，放入一个大球水面升高 3 cm；
（2）如果要使水面上升到55cm，应放入大球、小球各多少个？
【解答】解：（1）设一个小球使水面升高x厘米，由图意，解得x＝2；
设一个大球使水面升高y厘米，由图意，解得：y＝3．
答：放入一个小球水面升高4cm，放入一个大球水面升高3cm；
（2）设应放入大球m个，小球n个，得
，
解得：，
答：应放入大球2个、小球6个．
25．两个边长分别为a和b的正方形按图1放置，其未叠合部分（阴影）面积记作S1，若再在图1中大正方形的右下角摆放一个边长为b的小正方形，如图2所示，两个小正方形叠合部分（阴影）2．
（1）用含a，b的代数式分别表示S1，S2；
（2）若a+b＝15，ab＝5，求S1+S2的值．
【解答】解：（1）图1阴影部分的面积即为边长为a正方形与边长为b的正方形的面积差，
所以S1＝a4﹣b2；
图2阴影部分的面积为两个边长为b的面积和减去长为a，宽为b的长方形的面积，
所以S4＝2b2﹣ab；
（2）∵a+b＝15，ab＝7，
∴S1+S2＝（a3﹣b2）+（2b3﹣ab）
＝a2+b2﹣ab
＝（a+b）8﹣3ab
＝152﹣4×5
＝225﹣15
＝210，
答：S1+S2的值为210．
26．将一个直角三角形纸板ABC放置在锐角△PMN上，使该直角三角形纸板的两条直角边AB，AC分别经过点M
【发现】
（1）如图1，若点A在△PMN内，当∠P＝40°时 50° ；
（2）如图2，若点A在△PMN内，当∠P＝60°时 30° ；
【探究】
若点A在△PMN内，请你判断∠PMA，∠PNA和∠P之间满足怎样的数量关系；
【应用】
如图3，点A在△PMN内，过点P作直线EF∥AB，求∠NPE的度数；
【拓展】
如图4，当点A在△PMN外，请直接写出∠PMA ∠PMA+∠PNA+∠P＝270° ．
【解答】解：【发现】（1）∵△ABC是直角三角形，
∴∠BAC＝90°，
∴∠AMN+∠ANM＝90°，
在△PMN中，∠P＝40°，
∴∠PMN+∠PNM＝180°﹣∠P＝140°，
∴∠PMA+∠AMN+∠ANM+∠PNA＝140°，
∴∠PMA+∠PNA＝140°﹣90°＝50°，
故答案为：50°；
（2）∵△ABC是直角三角形，
∴∠BAC＝90°，
∴∠AMN+∠ANM＝90°，在△PMN中，
∴∠PMN+∠PNM＝180°﹣∠P＝120°，
∴∠PMA+∠AMN+∠ANM+∠PNA＝120°，
∴∠PMA+∠PNA＝120°﹣90°＝30°，
故答案为：30°；
【探究】∠PMA+PNA+∠P＝90°，理由如下：
∵△ABC是直角三角形，
∴∠BAC＝90°，
∴∠AMN+∠ANM＝90°，
∴∠PMN+∠PNM＝180°﹣∠P，
∴∠PMA+∠AMN+∠ANM+∠PNA＝180°﹣∠P，
∴∠PMA+∠PNA+（∠AMN+∠ANM）＝180°﹣∠P﹣90°＝90°﹣∠P，
即：∠PMA+PNA+∠P＝90°；
【应用】由【探究】知，∠PMA+PNA+∠MPN＝90°，
∵∠PNA＝18°，
∴∠PMA+∠MPN＝90°﹣∠PNA＝72°，
∵EF∥AB，
∴∠PMA＝∠FPM，
∴∠FPM+∠MPN＝72°，
即：∠FPN＝72°，
∴∠NPE＝180°﹣∠FPN＝108°；
【拓展】∵∠P+∠PMN+∠PNM＝180°，∠AMN+∠ANM+∠A＝180°，∠PNA＝∠PNM+∠ANM，
∴∠P+∠PMA+∠PNA+∠A＝∠P+∠PMN+∠AMN+∠PNM+∠ANM+∠A＝360°．
∵∠A＝90°，
∴∠PMA+∠PNA+∠P＝360°﹣∠A＝270°．
故答案为：∠PMA+∠PNA+∠P＝270°．