

- 重难点06 相交线与平行线的5种模型(5题型)-2024年中考数学一轮复习(全国通用) 试卷 4 次下载
- 重难点07 三角形的6种模型(A字、8字、飞镖、老鹰抓小鸡、双角平分线模型、三角形折叠)-2024年中考数学一轮复习讲练测(全国通用) 试卷 0 次下载
- 重难点09 相似三角形8种模型(A字、8字、射影定理、一线三等角等)-2024年中考数学一轮复习讲义(全国通用) 学案 5 次下载
- 重难点10 与四边形有关7种模型(垂美四边形、中点四边形、梯子模型等)-2024年中考数学一轮复习讲义(全国通用) 学案 3 次下载
- 重难点11 四边形压轴综合(17种题型)-2024年中考数学一轮复习讲练测(全国通用) 试卷 0 次下载
重难点08 全等三角形8种模型(一线三等角、手拉手模型、倍长中线等)-2024年中考数学一轮复习讲义(全国通用)
展开2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来,不等于“一点不懂、一点不会”,要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时,我们通常是将未知问题转化为已知的问题,将复杂的问题转化为简单的问题,将抽象的问题转化为具体的问题,将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题,把不熟悉的问题转化为熟悉的问题,把未知的问题转化为已知的问题。
重难点突破08 全等三角形8种模型
(一线三等角、手拉手模型、倍长中线、截长补短、婆罗摩笈多、半角模型、
平行线中点模型与雨伞模型)
目 录
TOC \ "1-3" \n \h \z \u
\l "_Tc156575233" 题型01 一线三等角模型(含一线三垂直模型)
\l "_Tc156575234" 题型02 手拉手模型
\l "_Tc156575235" 题型03 倍长中线模型
\l "_Tc156575236" 题型04 平行线中点模型与雨伞模型
\l "_Tc156575237" 题型05 截长补短模型
\l "_Tc156575238" 题型06 婆罗摩笈多模型
\l "_Tc156575239" 题型07 半角模型
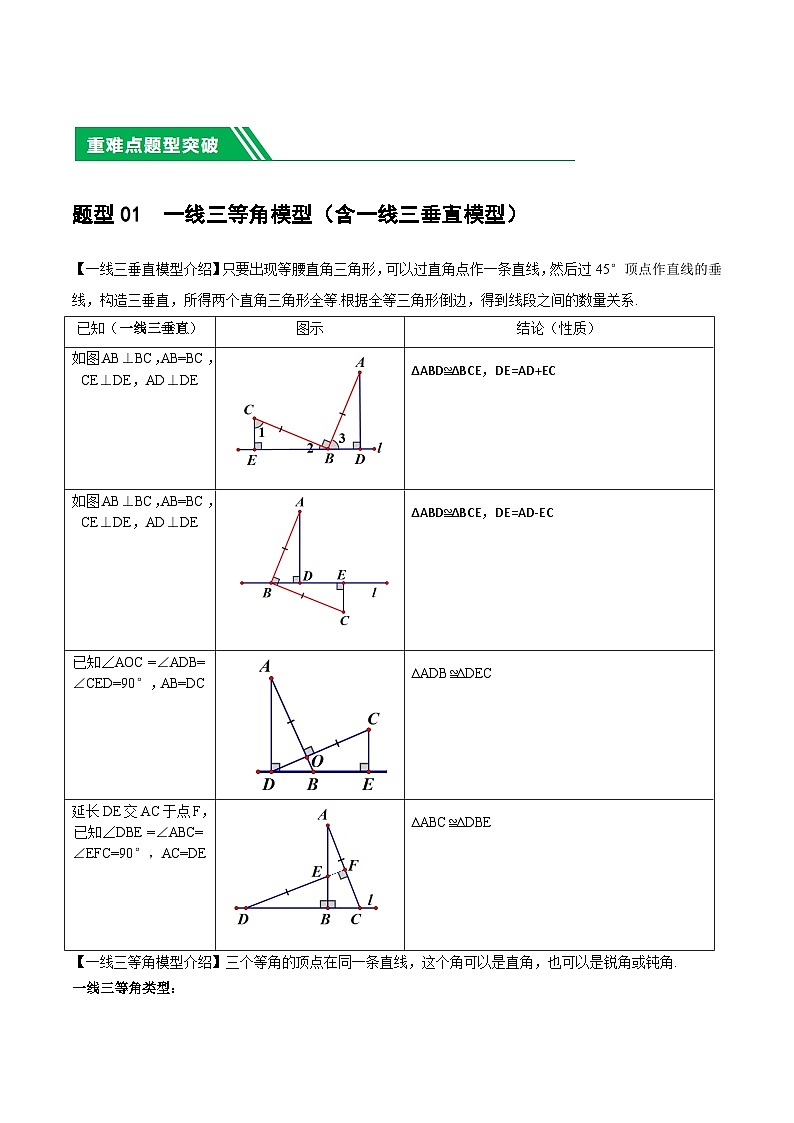
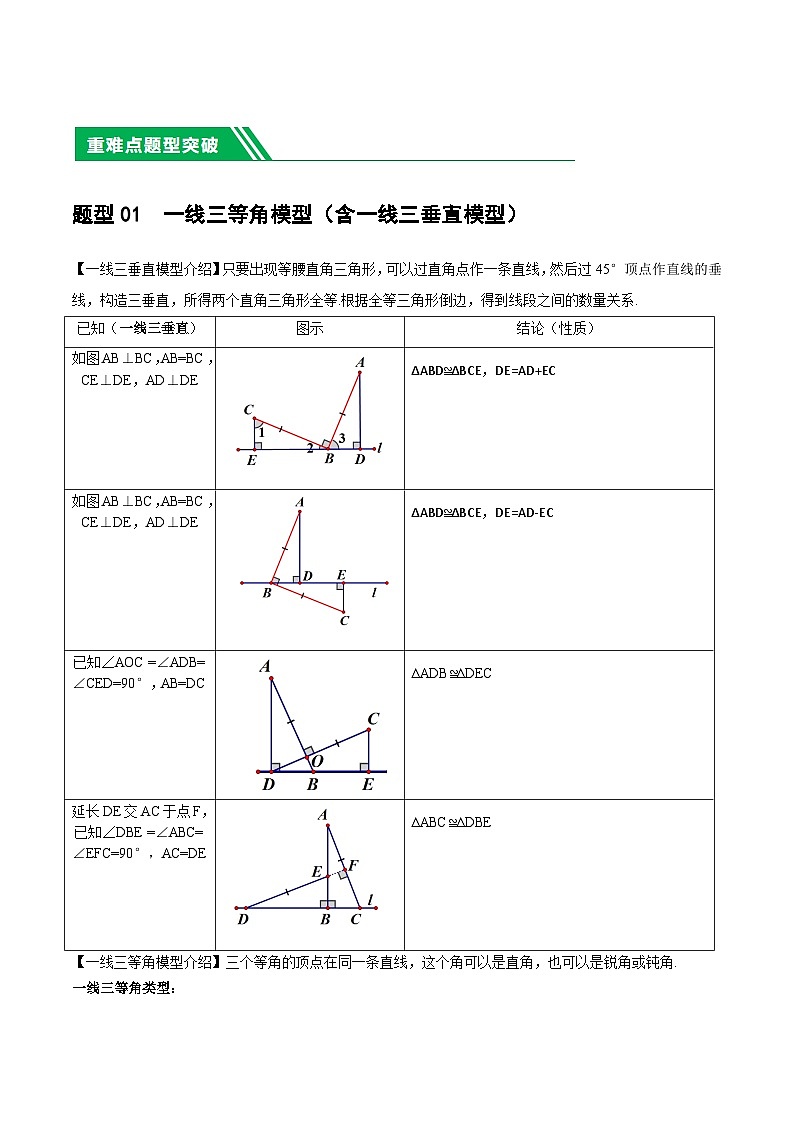
题型01 一线三等角模型(含一线三垂直模型)
【一线三垂直模型介绍】只要出现等腰直角三角形,可以过直角点作一条直线,然后过45°顶点作直线的垂线,构造三垂直,所得两个直角三角形全等.根据全等三角形倒边,得到线段之间的数量关系.
【一线三等角模型介绍】三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角.
一线三等角类型:
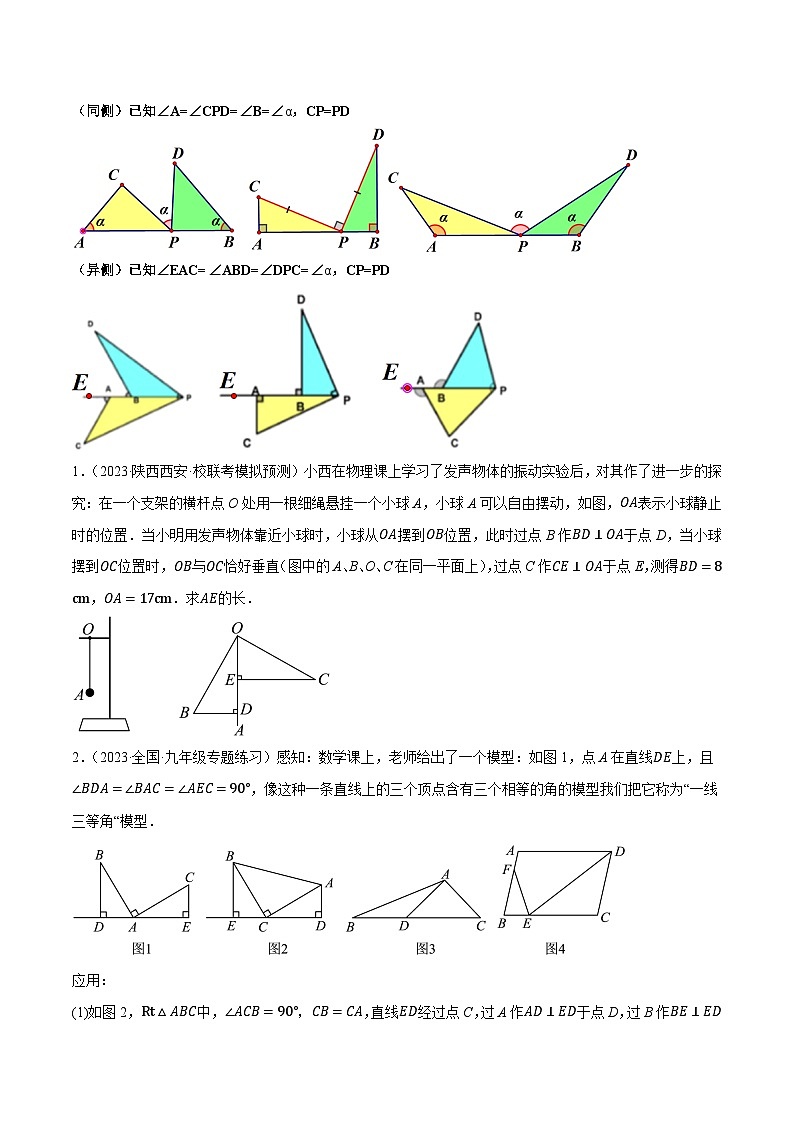
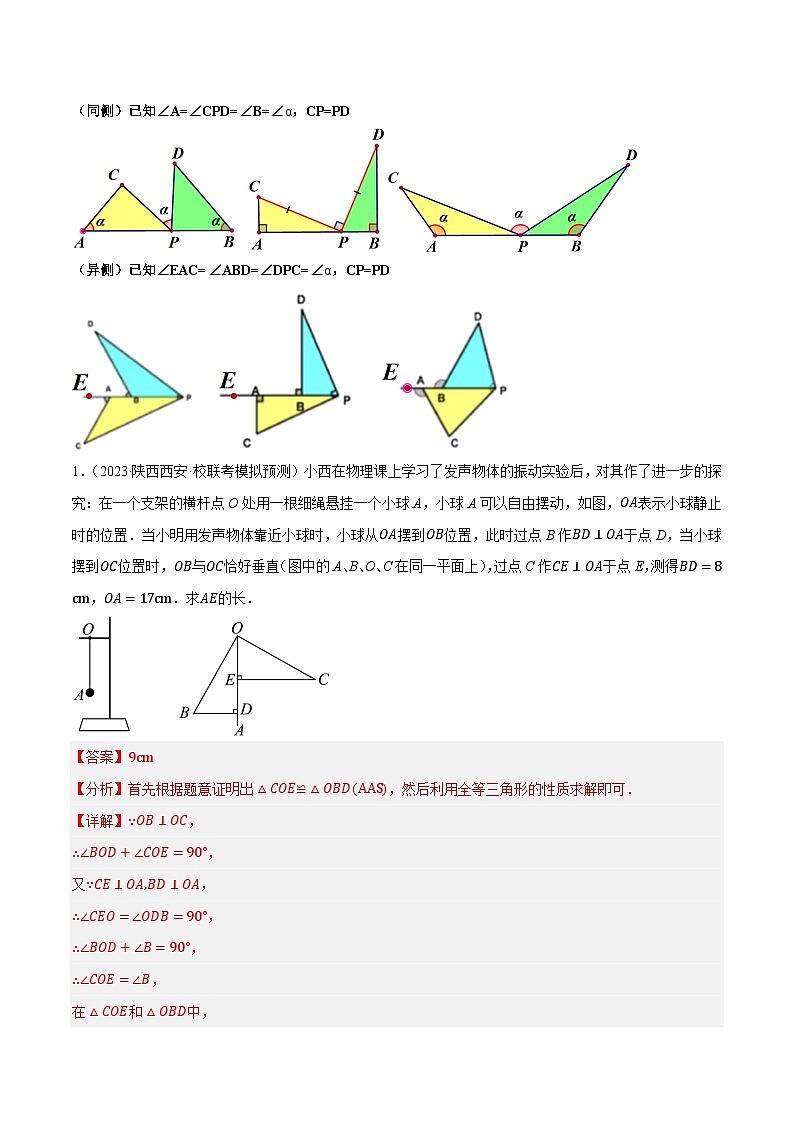
(同侧)已知∠A=∠CPD=∠B=∠α,CP=PD
(异侧)已知∠EAC=∠ABD=∠DPC=∠α,CP=PD
1.(2023·陕西西安·校联考模拟预测)小西在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A、B、O、C在同一平面上),过点C作CE⊥OA于点E,测得BD=8cm,OA=17cm.求AE的长.
2.(2023·全国·九年级专题练习)感知:数学课上,老师给出了一个模型:如图1,点A在直线DE上,且∠BDA=∠BAC=∠AEC=90°,像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
应用:
(1)如图2,Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA.
(2)如图3,在△ABC中,D是BC上一点,∠CAD=90°,AC=AD,
∠DBA=∠DAB,AB=23,求点C到AB边的距离.
(3)如图4,在▱ABCD中,E为边BC上的一点,F为边AB上的一点.若
∠DEF=∠B,AB=10,BE=6,求 EFDE的值.
3.(2022·北京·校考一模)对于平面直角坐标系xOy中的图形M和点P,给出如下定义:将图形M绕点P顺时针旋转90°得到图形N,图形N称为图形M关于点P的“垂直图形”.例如,图1中点D为点C关于点P的“垂直图形”.
(1)点A关于原点O的“垂直图形”为点B.
①若点A的坐标为0,3,则点B的坐标为___________;
②若点B的坐标为3,1,则点A的坐标为___________;
(2)E(−3,3),F(−2,3),G(a,0),线段EF关于点G的“垂直图形”记为E'F',点E的对应点为E',点F的对应点为F'.
①求点E'的坐标(用含a的式子表示);
②若⊙O的半径为2,E'F'上任意一点都在⊙O内部或圆上,直接写出满足条件的EE'的长度的最大值.
4.(2021·浙江嘉兴·校考一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC中,∠ACB=90°,AC=BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:△ADC≌△CEB.
(1)探究问题:如果AC≠BC,其他条件不变,如图②,可得到结论;△ADC∽△CEB.请你说明理由.
(2)学以致用:如图③,在平面直角坐标系中,直线y=12x与直线CD交于点M(2,1),且两直线夹角为α,且tanα=32,请你求出直线CD的解析式.
(3)拓展应用:如图④,在矩形ABCD中,AB=4,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC,PD.若△DPC为直角三角形时,请你探究并直接写出BE的长.
5.(2022下·安徽淮北·九年级校联考阶段练习)数学模型学习与应用.【学习】如图1,∠BAD=90°,AB=AD,BC⊥AC于点C,DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通过推理得到△ABC≌△DAE.我们把这个数学模型称为“一线三等角”模型;
(1)【应用】如图2,点B,P,D都在直线l上,并且∠ABP=∠APC=∠PDC=α.若BP=x,AB=2,BD=5,用含x的式子表示CD的长;
(2)【拓展】在△ABC中,点D,E分别是边BC,AC上的点,连接AD,DE,∠B=∠ADE=∠C,AB=5,BC=6.若△CDE为直角三角形,求CD的长;
(3)如图3,在平面直角坐标系xOy中,点A的坐标为2,4,点B为平面内任一点.△AOB是以OA为斜边的等腰直角三角形,试直接写出点B的坐标.
6.(2021上·山东青岛·九年级统考期中)【模型引入】
我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形,可以使得我们在观察新问题的时候很迅速地联想,从而借助已有经验,迅速解决问题.
【模型探究】
如图,正方形ABCD中,E是对角线BD上一点,连接AE,过点E作EF⊥AE,交直线CB于点F.
(1)如图1,若点F在线段BC上,写出EA与EF的数量关系并加以证明;
(2)如图2,若点F在线段CB的延长线上,请直接写出线段BC,BE和BF的数量关系.
【模型应用】
(3)如图3,正方形ABCD中,AB=4,E为CD上一动点,连接AE交BD于F,过F作FH⊥AE于F,过H作HG⊥BD于G.则下列结论:①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH的周长为8.正确的结论有 个.
(4)如图4,点E是正方形ABCD对角线BD上一点,连接AE,过点E作EF⊥AE,交线段BC于点F,交线段AC于点M,连接AF交线段BD于点H.给出下列四个结论,①AE=EF;②2DE=CF;③S△AEM=S△MCF;④BE=DE+2BF;正确的结论有 个.
【模型变式】
(5)如图5,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线与点N,求证:MD=MN
(6)如图6,在上一问的条件下,连接DN交BC于点F,连接FM,则∠FMN和∠NMB之间有怎样的数量关系?请给出证明.
【拓展延伸】
(7)已知∠MON=90°,点A是射线ON上的一个定点,点B是射线OM上的一个动点,且满足OB>OA.点C在线段OA的延长线上,且AC=OB.如图7,在线段BO上截取BE,使BE=OA,连接CE.若∠OBA+∠OCE=β,当点B在射线OM上运动时,β的大小是否会发生变化?如果不变,请求出这个定值;如果变化,请说明理由.
(8)如图8,正方形ABCD中,AD=6,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EDM的面积是 .
7.(2022上·吉林长春·七年级长春市第四十五中学校考期中)通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
[模型呈现]如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.求证:BC=AE.
[模型应用]如图2,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积为________________.
[深入探究]如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.若BC=21,AF=12,则△ADG的面积为_____________.
8.(2020上·河南安阳·八年级统考期末)(1)如图①.已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.则线段DE、BD与CE之间的数量关系是______;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问:(1)中的结论是还否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图③,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE.若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
9.(2023上·湖南长沙·八年级统考阶段练习)如图,在平面直角坐标系中,点Ba,b是第二象限内一点.
(1)若a、b满足等式a+32+b−2=0,求点B的坐标;
(2)如图1,在(1)的条件下,动点C以每秒2个单位长度的速度从O点出发,沿x轴的负半轴方向运动,同时动点A以每秒1个单位长度的速度从O点出发,沿y轴的正半轴方向运动,设运动的时间为t秒,当t为何值时,△ABC是AB为斜边的等腰直角三角形;
(3)如图2,C、A分别是x轴负半轴和y轴上正半轴上一点,且△ABC是以AB为斜边的等腰直角三角形,若E是线段OC上一点,连接BE交AC于点D,连接AE,当AE=CE,∠OAE=45∘,①求证:BE平分∠ABC; ②设BD的长为a,△ADB的面积为S.请用含a的式子表示S.
10.(2022上·江苏南京·八年级校考阶段练习)已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE=9cm,∠BDA=∠AEC=∠BAC.
(1)如图①,若AB⊥AC,则BD与AE的数量关系为 ___________,CE与AD的数量关系为 ___________;
(2)如图②,判断并说明线段BD,CE与DE的数量关系;
(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.
题型02 手拉手模型
【模型介绍】两个顶角相等的等腰三角形共用顶角顶点,分别连接对应的两底角顶点,从而可以得到一个经典的全等模型.因为顶点相连的四条边,形象可以看作两双手,通常称为“手拉手模型”.
文字说明:1)点A 为共用顶角顶点,看作头
2)线段AB、AC为等腰∆ABC的两腰,看作两条手臂
线段AM、AN为等腰∆AMN的两腰,看作两条手臂
3)点B与点M看作左手,线段BM看作左手拉左手
点C与点N看作右手,线段CN看作右手拉右手
解题步骤:①找共用顶点,确定“四只手”;
②连接对应端点;
③SAS证明全等.
11.(2023·安徽黄山·校考一模)已知△ABC和△ADE均为等腰直角三角形,△ADE绕点A逆时针旋转一周.
(1)如图1,连接BD,CE,则BD与CE的数量关系为_______;直线BD与CE所夹角的度数为_______.
(2)当△ADE旋转至如图2所示的位置时,取BC,DE的中点M,N,连接MN,BD.试问:MNBD的值是否随△ADE的旋转而变化?若不变,请求出该值;若变化,请说明理由.
(3)M,N分别为BC,DE的中点,连接MN.若AB=310,AD=6,当△ADE旋转至B,D,E三点在同一条直线上时,请直接写出MN的值.
12.(2023下·江西抚州·九年级校考阶段练习)在△ABC中,AB=AC,∠BAC=α,点P是平面内不与点A,C重合的任意一点,连接PC,将线段PC绕点P旋转α得到线段PD,连接AP、CD、BD.
(1)当α=60°时,
①如图1,当点P在△ABC的边BC上时,线段PC绕点P顺时针旋转α得到线段PD,则AP与BD的数量关系是_______________;
②如图2,当点P在△ABC内部时,线段PC绕点P顺时针旋转α得到线段PD,①中AP与BD的数量关系还成立吗?若成立,请证明结论,若不成立,说明理由;
(2)当α=90°时,
①如图3,线段PC绕点P顺时针旋转α得到线段PD.试判断AP与BD的数量关系,并说明理由;
②若点A,C,P在一条直线上,且AC=3PC,线段PC绕点P逆时针旋转α得到线段DP,求BDAP的值.
13.(2023·河南洛阳·统考模拟预测)综合与实践综合与实践课上,数学研究小组以“手拉手图形”为主题开展数学活动两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)操作判断 已知点C为△ABC和△CDE的公共顶点,将△CDE绕点C顺时针旋转α0°
②直线BD与直线AE相交所夹锐角的度数是________;
(2)迁移探究 如图2,若∠ABC=∠EDC=90°,∠BAC=∠DEC=30°,其他条件不变,则(1)中的结论是否都成立?请说明理由;
(3)拓展应用:如图3,若∠BAC=∠DEC=90°,AB=AC,CE=DE,BC=2CD=42,当点B,D,E三点共线时,请直接写出BD的长.
14.(2023·河南郑州·郑州市第八中学校考二模)由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形,如果把它们的底角顶点连接起来,则在相对位置变化的过程中,始终存在一对全等三角形,我们把这种模型称为“手拉手模型”.
(1)【问题发现】
如图1所示,两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD、CE,两线交于点P,BD和CE的数量关系是 ;BD和CE的位置关系是 ;
(2)【类比探究】
如图2所示,点P是线段AB上的动点,分别以AP、BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC、PC于点M、N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出DHBC的值;
(3)【拓展延伸】
如图3所示,已知点C为线段AE上一点,AE=6,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN,直接写出线段MN的最大值.
15.(2022·青海·统考中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.
(1)问题发现:
如图1,若△ABC和△ADE是顶角相等的等腰三角形,BC,DE分别是底边.求证:BD=CE;
图1
(2)解决问题:如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.
图2
16.(2019·山东济宁·统考三模)背景材料:
在学习全等三角形知识时,数学兴趣小组发现这样一个模型,它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们知道这种模型称为手拉手模型.
例如:如图1,两个等腰直角三角形△ABC和△ADE,∠BAC=∠EAD=90°,AB=AC,AE=AD,如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是手拉手模型,在这个模型中易得到△ABD≌△ACE.
学习小组继续探究:
(1)如图2,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,请作出一个手拉手图形(尺规作图,不写作法,保留作图痕迹),并连接BE,CD,证明BE=CD;
(2)小刚同学发现,不等腰的三角形也可得到手拉手模型,例如,在△ABC中AB>AC,DE∥BC,将三角形ADE旋转一定的角度(如图3),连接CE和BD,证明△ABD∽△ACE.
学以致用:
(3)如图4,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα=34,CD=5,AD=12.请在图中构造小刚发现的手拉手模型求BD的长.
17.(2023·黑龙江大庆·统考中考真题)如图,在△ABC中,将AB绕点A顺时针旋转α至AB',将AC绕点A逆时针旋转β至AC'(0°<α<180°,0°<β<180°),得到△AB'C',使∠BAC+∠B'AC'=180°,我们称△AB'C'是△ABC的“旋补三角形”,△AB'C'的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .
①△ABC与△AB'C'面积相同;
②BC=2AD;
③若AB=AC,连接BB'和CC',则∠B'BC+∠CC'B'=180°;
④若AB=AC,AB=4,BC=6,则B'C'=10.
18.(2022·江苏淮安·统考二模)在学习全等三角形知识时,数学兴趣小组发现这样一个模型:模型是由两个顶角相等且有公共顶角顶点的等腰三角形组成的图形,如果把它们的底角顶点连接起来,则在相对位置变化的过程中,始终存在一对全等三角形,我们把这种模型称为“手拉手模型”.这个数学兴趣小组进行了如下操作:
(1)如图1、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD,CE,两线交于点P,和△ABD全等的三角形是______,BD和CE的数量关系是________.
(2)如图2,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出DHBC的值.
(3)如图3,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN,线段MN的最大值是______.
19.(2020·吉林长春·统考一模)[问题提出]
(1)如图①,△ABC、△ADE均为等边三角形,点D、E分别在边AB、AC上.将△ADE绕点A沿顺时针方向旋转,连结BD、CE.在图②中证明△ADB≌△AEC.
[学以致用]
(2)在1的条件下,当点D、E、C在同一条直线上时,∠EDB的大小为 度.
[拓展延伸]
(3)在1的条件下,连结CD.若BC=6,AD=4,直接写出△DBC的面积S的取值范围.
20.(2022·山东烟台·统考中考真题)
(1)【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
(2)【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出BDCE的值.
(3)【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且ABBC=ADDE=34.连接BD,CE.
①求BDCE的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
21.(2020·广东深圳·统考中考真题)背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了三个问题,请你帮助解答:
(1)将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:
(2)把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;
(3)把背景中的正方形改成矩形AEFG和矩形ABCD,且AEAG=ABAD=23,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.
22.(2022·浙江湖州·统考中考真题)已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.
(1)如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1,正方形BGFC的面积为S2.
①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2−S1=2S.
(2)如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1,等边三角形CBE的面积为S2.以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2−S1与S之间的等量关系,并说明理由.
.题型03 倍长中线模型
【模型介绍】当遇见中线或者中点的时候,可以尝试倍长中线或类中线,使得延长后的线段是原中线的二倍,从而构造一对全等三角形(SAS),并将已知条件中的线段和角进行转移.
23.(2019·山东淄博·统考一模)如图,ΔABC中,D为BC的中点,E是AD上一点,连接BE并延长交AC于F,BE=AC,且BF=9,CF=6,那么AF的长度为 .
24.(2020上·北京朝阳·八年级统考期末)阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
25.(2020上·河北邢台·八年级校考期中)某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.
【探究与发现】
(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,证明:△ACD≌△EBD.
【理解与应用】
(2)如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是________.
(3)如图3,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,求证:BE+CF>EF.
26.(2020·江苏徐州·统考模拟预测)(1)阅读理解:
如图①,在△ABC中,若AB=8,AC=5,求BC边上的中线AD的取值范围.可以用如下方法:将△ACD绕着点D逆时针旋转180∘得到△EBD,在△ABE中,利用三角形三边的关系即可判断中线AD的取值范围是_______;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=100°,以C为顶点作一个50°的角,角的两边分别交AB、AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并说明理由.
27.(2016·贵州贵阳·中考真题)阅读
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是________;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
28.(2020上·山西吕梁·八年级统考期中)阅读下列材料,完成相应任务.
数学活动课上,老师提出了如下问题:
如图1,已知ΔABC中,AD是BC边上的中线.
求证:AB+AC>2AD.
智慧小组的证法如下:
证明:如图2,延长AD至E,使DE=AD,
∵AD是BC边上的中线∴BD=CD
在ΔBDE和ΔCDA中BD=CD∠BDE=∠CDADE=DA
∴ΔBDE≌ΔCDA(依据一)∴BE=CA
在ΔABE中,AB+BE>AE(依据二)
∴AB+AC>2AD.
任务一:上述证明过程中的“依据1”和“依据2”分别是指:
依据1:______________________________________________;
依据2:______________________________________________.
归纳总结:上述方法是通过延长中线AD,使DE=AD,构造了一对全等三角形,将AB,AC,AD转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
任务二:如图3,AB=3,AC=4,则AD的取值范围是_____________;
任务三:如图4,在图3的基础上,分别以AB和AC为边作等腰直角三角形,在RtΔABE中,∠BAE=90°,AB=AE;RtΔACF中,∠CAF=90°,AC=AF.连接EF.试探究EF与AD的数量关系,并说明理由.
题型04 平行线中点模型与雨伞模型
【平行线中点模型介绍】平行线之间夹中点,通过延长过中点的线段与平行线相交,从而构造一对全等三角形,并将已知条件中的线段和角进行转移。
29.(2021上·江苏苏州·八年级统考期中)如图,△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1)线段BE与线段AD有何数量关系?并说明理由;
(2)判断△BEG的形状,并说明理由.
30.(2021上·江苏南京·八年级统考期中)如图,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.求证:BE=12CD.
31.(2018下·四川成都·七年级统考期末)如图1,点A是直线MN上一点,点B是直线PQ上一点,且MN//PQ.∠NAB和∠ABQ的平分线交于点C.
(1)求证:BC⊥AC;
(2)过点C作直线交MN于点D(不与点A重合),交PQ于点E,
①若点D在点A的右侧,如图2,求证:AD+BE=AB;
②若点D在点A的左侧,则线段AD、BE、AB有何数量关系?直接写出结论,不说理由.
32.(2020·全国·九年级专题练习)如图,已知等腰直角三角形ABC中,AB=AC,∠BAC=90°,BF平分∠ABC,CD⊥BD交BF的延长线于点D,试说明:BF=2CD.
题型05 截长补短模型
模型的概述:该模型适用于求证线段的和差倍分关系,该类题目中常出现等腰三角形、角平分线等关键词,可以采用截长补短法构造全等三角形来完成证明。其中截长指在长线段中截取一段等于已知线段,补短指将短线段延长,使短线段加上延长线段长度等于长线段。
图解:已知线段AB、CD、EF,简述利用截长补短法证明AB=CD+EF的方法
截长法:在线段AB上,截取AG=CD,判断线段GB和线段EF长度是否相等
补短法:延长线段CD至点H,使DH=EF,判断线段AB和线段GH长度是否相等
33.(2020上·山东济南·八年级统考期末)【阅读理解】截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是______;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为4cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长为______cm.
34.(2022上·湖北孝感·八年级统考期中)如图,在五边形ABCDE中,AB=AE,CA平分∠BCD,∠CAD=12∠BAE.
(1)求证:CD=BC+DE;
(2)若∠B=75°,求∠E的度数.
35.(2022上·湖北孝感·八年级统考期中)如图,在四边形ABCD中,AC与BD交于点O,AC平分∠DAB,BD平分∠CBA,∠ADC+∠BCD=240°.
(1)求∠AOB的度数;
(2)求证:OD=OC.
36.(2018上·江苏盐城·八年级校联考期末)例:截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:将△ABD绕点A逆时针旋转60°得到△ACE,可得AE=AD, CE=BD,∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则 ∠ACE+∠ACD=180°,易知△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.
37.(2020·辽宁沈阳·统考一模)思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.
38.(2021·重庆沙坪坝·重庆八中校考一模)如图1,在四边形ABCD中,AC交BD于点E,△ADE为等边三角形.
(1)若点E为BD的中点,AD=4,CD=5,求△BCE的面积;
(2)如图2,若BC=CD,点F为CD的中点,求证:AB=2AF;
(3)如图3,若AB∥CD,∠BAD=90°,点P为四边形ABCD内一点,且∠APD=90°,连接BP,取BP的中点Q,连接CQ.当AB=62,AD=42,tan∠ABC=2时,求CQ+1010BQ的最小值.
题型06 婆罗摩笈多模型
婆罗摩笈多模型条件:1)公共顶点:顶点C
2)等线段:BC=DC CE=CG
3)顶角相等:∠DCB=∠GCE=90°
39.(2021上·重庆开州·八年级校联考期中)如图,在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE 和ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论是( )
A.①②③B.①②④C.①③④D.①②③④
40.(2023上·山西太原·九年级成成中学校考阶段练习)综合与实践
以△ABC的两边AB、AC为边,向外作正方形ABDE和正方形ACFG,连接EG,过点A作AM⊥BC于M,延长MA交EG于点N.
(1)如图①,若AB=AC,证明:EN=GN;
(2)如图②,∠BAC=90°,(1)中结论,是否成立,若成立,请证明;若不成立,写出你的结论,并说明理由;
(3)如图③,∠BAC≠90°,AB=5,AC=10,且AM=3,则S△AEG=________________.
41.(2017·江西·中考真题)我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=23,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
42.(2019上·湖北十堰·九年级校联考期末)已知,△ABC中,BC=6,AC=4,M是BC的中点,分别以AB,AC为边向外作正方形ABDE,正方形ACFG,连接EG,MA的延长线交EG于点N,
(1)如图,若∠BAC=90°,求证:AM=12EG,AM⊥EG;
(2)将正方形ACFG绕点A顺时针旋转至如图,(1)中结论是否仍然成立?请说明理由;
(3)将正方形ACFG绕点A顺时针旋转至B,C,F三点在一条直线上,请画出图形,并直接写出AN的长.
43.(2020·全国·九年级专题练习)如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中BC边上的中线,延长MA交EG于点H.
求证:
(1)AM=12EG;
(2)AH⊥EG;
(3)EG2+BC2=2(AB2+AC2).
题型07 半角模型
半角模型的概述:当一个角包含着该角的半角,如90°角包含着45°角,120°角包含着60°角,270°角包含着135°角,即出现12倍角关系,且这两个角共顶点,共顶点的两条边相等,则该模型为半角模型。解题方法为:1)过公共点作旋转,2)截长补短的方法构造全等解题。
44.(2022上·广西南宁·九年级统考期中)【探索发现】如图①,四边形ABCD是正方形,M,N分别在边CD、BC上,且∠MAN=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图①,将△ADM绕点A顺时针旋转90°,点D与点B重合,得到△ABE,连接AM、AN、MN.
(1)试判断DM,BN,MN之间的数量关系,并写出证明过程.
(2)如图②,点M、N分别在正方形ABCD的边BC、CD的延长线上,∠MAN=45°,连接MN,请写出MN、DM、BN之间的数量关系,并写出证明过程.
45.(2022·江西南昌·模拟预测)【模型建立】
(1)如图1,在正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,探究图中线段EF,BE,DF之间的数量关系.
小明的探究思路如下:延长CB到点G,使BG=DF,连接AG,先证明△ADF≌△ABG,再证明△AEF≌△AEG.
①EF,BE,DF之间的数量关系为________;
②小亮发现这里△ABG可以由△ADF经过一种图形变换得到,请你写出这种图形变换的过程________.像上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型.
【类比探究】
(2)如图2,在四边形ABCD中,AB=AD,∠ABC与∠D互补,E,F分别是边BC,CD上的点,且∠EAF=12∠BAD,试问线段EF,BE,DF之间具有怎样的数量关系?判断并说明理由.
【模型应用】
(3)如图3,在矩形ABCD中,点E在边BC上,AD=6,AB=4,∠CAE=45°,求CE的长.
46.(2020下·江苏盐城·九年级统考阶段练习)已知如图1,四边形ABCD是正方形,E,F分别在边BC、CD上,且∠EAF=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
(1)在图l中,连接EF,为了证明结论“EF=BE+DF”,小亮将ΔADF绕点A顺时针旋转90°后解答了这个问题,请按小亮的思路写出证明过程;
(2)如图2,当∠EAF绕点A旋转到图2位置时,试探究EF与DF、BE之间有怎样的数量关系?
(3)如图3,如果四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45∘,且BC=7,DC=13,CF=5,求BE的长.
47.(2021上·江苏南通·八年级校考阶段练习)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=12∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
48.(2022上·河北邢台·九年级统考期末)学完旋转这一章,老师给同学们出了这样一道题:
“如图1,在正方形ABCD中,∠EAF=45°,求证:EF=BE+DF.”
小明同学的思路:∵四边形ABCD是正方形,∴AB=AD,∠B=∠ADC=90°.
把△ABE绕点A逆时针旋转到△ADE'的位置,然后证明△AFE≌△AFE',从而可得EF=E'F.
E'F=E'D+DF=BE+DF,从而使问题得证.
(1)【探究】请你参考小明的解题思路解决下面问题:
如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠EAF=12∠BAD,直接写出EF,BE,DF之间的数量关系.
(2)【应用】如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,∠EAF=12∠BAD,求证:EF=BE+DF.
(3)【知识迁移】如图4,四边形ABPC是⊙O的内接四边形,BC是直径,AB=AC,请直接写出PB+PC与AP的关系.
49.(2021上·浙江绍兴·八年级校联考期中)问题情境
在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.
特例探究
如图1,当DM=DN时,
(1)∠MDB= 度;
(2)MN与BM,NC之间的数量关系为 ;
归纳证明
(3)如图2,当DM≠DN时,在NC的延长线上取点E,使CE=BM,连接DE,猜想MN与BM,NC之间的数量关系,并加以证明.
拓展应用
(4)△AMN的周长与△ABC的周长的比为 .
50.(2022上·山西·九年级统考期末)阅读以下材料,并按要求完成相应的任务:
任务:
如图3,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BAD=120°,以A为顶点的∠EAF=60°,AE、AF与BC、CD边分别交于E、F两点.请参照阅读材料中的解题方法,你认为结论EF=BE+DF是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.
51.(2022上·江苏扬州·八年级校考阶段练习)(1)【阅读理解】如图,已知△ABC中,AB=AC,点D、E是边BC上两动点,且满足∠DAE=12∠BAC,
求证:BD+CE>DE.
我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
小明的解题思路:将半角∠DAE两边的三角形通过旋转,在一边合并成新的△AFE,然后证明与半角形成的△ADE全等,再通过全等的性质进行等量代换,得到线段之间的数量关系.
请你根据小明的思路写出完整的解答过程.
证明:将△ABD绕点A旋转至△ACF,使AB与AC重合,连接EF,
……
(2)【应用提升】如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD点D运动;点Q点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE与CD相交于点F,连接PF,设点P运动时间为ts,
①求∠PBE的度数;
②试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
52.(2020上·重庆璧山·九年级重庆市璧山中学校校考阶段练习)“半角型”问题探究:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
(1)小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE≌△AFG,从而得出结论:
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=12∠BAD,上述结论是否仍然成立,并说明理由.
(3)如图3,边长为4的正方形ABCD中,点E、F分别在AB、CD上,AE=CF=1,O为EF的中点,动点G、H分别在边AD、BC上,EF与GH的交点P在O、F之间(与O、F不重合),且∠GPE=45°,设AG=m,求m的取值范围.
已知(一线三垂直)
图示
结论(性质)
如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE
∆ABD≌∆BCE,DE=AD+EC
如图AB⊥BC,AB=BC,CE⊥DE,AD⊥DE
∆ABD≌∆BCE,DE=AD-EC
已知∠AOC =∠ADB=∠CED=90°,AB=DC
∆ADB≌∆DEC
延长DE交AC于点F,已知∠DBE =∠ABC=∠EFC=90°,AC=DE
∆ABC≌∆DBE
已知
图示
结论(性质)
如图,直线AB的同一侧作∆ABC和∆AMN都为等边三角形(A、B、N三点共线),连接BM、CN,两者相交于点E
1)∆ABM≌∆ACN 2)BM=CN
3)∠MEN=∠2=60°(拉手线的夹角等于顶角)
4)∆ANF≌∆AMD 5)∆AFC≌∆ADB 6)连接DF,DF∥BN 7)连接AE,AE平分∠BEN 8)存在3组四点共圆 9)EN=EM+EA,EB=EC+EA,EA=ED+EF
如图,∆ABC和∆AMN都为等边三角形(A、B、N三点不共线),连接BM、CN,两者相交于点O
1)∆ABM≌∆ACN 2)BM=CN
3)∠MON=60°(拉手线的夹角等于顶角)
4)连接AO,AO平分∠BON
5)存在2组四点共圆
6)ON=OM+OA,OB=OC+OA
如图,四边形ABCD和四边形AEFG为正方形,连接EB和GD,两者交于点O
1)∆AGD≌∆AEB 2)GD=EB
3)GD⊥EB 4)AO平分∠EOD
已知
图示
结论(性质)
已知点D为∆ABC中BC边中点,延长线段AD到点E使AD=DE
1)连接EC,则∆ABD≌∆ECD,AB∥CE
2)连接BE,则∆ADC≌∆EDB,AC∥BE
已知点D为∆ABC中BC边中点,延长线段DF到点E使DF=DE,
连接EC
∆BDF≌∆CDE
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
已知
图示
结论(性质)
已知AB∥CD,点E,F分别在直线AB、CD上,点O为线段EF的中点,延长PO交CD于点Q
∆POE ≌ ∆QOF
如图AP平分∠BAC,BD⊥AP,垂足为点D,延长BD交AC于点C
∆ABD ≌ ∆ACD,AB=AC,BD=CD
已知
图示
结论(性质)
四边形ABCD、CEFG为正方形,连接BE、DG,I、C、H三点共线,若点I为中点
CH⊥BE,BE=2IC,S∆DCG=S∆BCE
四边形ABCD、CEFG为正方形,连接BE、DG,I、C、H三点共线,若CH⊥BE
点I为中点,BE=2IC,S∆DCG=S∆BCE
已知
图示
结论(性质)
[90°半角模型]已知正方形ABCD中,E,F分别是BC、CD上的点,∠EAF=45°,AE、AF分别与BD相交于点O、P
①EF=BE+DF ②AE平分∠BEF,AF平分∠DFE
③C∆CEF=2倍正方形边长 ④S∆ABE +S∆ADF =S∆AEF ⑤AB=AG=AD(过点A作AG⊥EF,垂足为点G)
⑥OP2=OB2+OD2 ⑦若点E为BC中点,则点F为CD三等分点
⑧∆APO∽∆AEF∽∆DPF∽∆BEO∽∆DAO∽∆BPA
⑨ABEP四点共圆、AOFD四点共圆、OECFP五点共圆
⑩∆APE、∆AOF为等腰直角三角形 (11) EF=2OP
(12) S∆AEF=2S∆APO (13)AB2=BP×OD
(14)CE•CF=2BE•DF (15) ∆EPC为等腰三角形
(16) PX=BX+DP(过点E作EX⊥BD,垂足为点X)
[120°半角模型] 已知∆ABC为等边三角形,DB=DC,∠BDC=120°,∠MDN=60°
MN=NC-BM
[135°半角模型] 在Rt∆ABC中,点E、点D分别为AB、AC边上动点,四边形AEFD是正方形,且∠BFC=135°
CB=CD+BE
从正方形的一个顶点引出夹角为45°的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:
如图1,在正方形ABCD中,以A为顶点的∠EAF=45°,AE、AF与BC、CD边分别交于E、F两点.易证得EF=BE+FD.
大致证明思路:如图2,将△ADF绕点A顺时针旋转90°,得到△ABH,由∠HBE=180°可得H、B、E三点共线,∠HAE=∠EAF=45°,进而可证明△AEH≌△AEF,故EF=BE+DF.
重难点07 三角形的6种模型-2024年中考数学一轮复习讲义(全国通用): 这是一份重难点07 三角形的6种模型-2024年中考数学一轮复习讲义(全国通用),文件包含重难点突破07三角形的6种模型A字8字飞镖老鹰抓小鸡双角平分线模型三角形折叠原卷版docx、重难点突破07三角形的6种模型A字8字飞镖老鹰抓小鸡双角平分线模型三角形折叠解析版docx等2份学案配套教学资源,其中学案共81页, 欢迎下载使用。
2024年中考数学常见几何模型全等模型-倍长中线与截长补短模型-学案(学生+教师版): 这是一份2024年中考数学常见几何模型全等模型-倍长中线与截长补短模型-学案(学生+教师版),文件包含全等模型-倍长中线与截长补短模型解析版pdf、全等模型-倍长中线与截长补短模型学生版pdf等2份学案配套教学资源,其中学案共50页, 欢迎下载使用。
【期末满分攻略】2022-2023学年北师大版七年级数学下册讲学案-专题13 全等三角形重难点模型(五大模型)(原卷版+解析版): 这是一份【期末满分攻略】2022-2023学年北师大版七年级数学下册讲学案-专题13 全等三角形重难点模型(五大模型)(原卷版+解析版),文件包含期末满分攻略2022-2023学年北师大版七年级数学下册讲学案-专题13全等三角形重难点模型五大模型解析版docx、期末满分攻略2022-2023学年北师大版七年级数学下册讲学案-专题13全等三角形重难点模型五大模型原卷版docx等2份学案配套教学资源,其中学案共83页, 欢迎下载使用。












