河北省承德市承德县第二中学2022-2023学年九年级下学期月考数学试卷(含答案)

这是一份河北省承德市承德县第二中学2022-2023学年九年级下学期月考数学试卷(含答案)，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．计算( )
A.mB.3mC.D.
2．如图，光线自点P射入，经镜面EF反射后经过的点是( )
A.A点B.B点C.C点D.D点
3．若“□”的值为负数，则“□”不可能是( )
A.－1B.0C.D.3
4．如图，在中，线段的长度可以表示点A到的距离，则是的( )
A.中线B.高线C.角平分线D.中位线
5．下列计算正确的是( )
A.B.C.D.
6．若等式根据等式的性质变形得到，则a、b满足的条件是( )
A.相等B.互为倒数C.互为相反数D.无法确定
7．2022年9月29日，据银保监会统计，前8个月我国保险业实现原保险保费收入3.46万亿元，赔付支出1.02万亿元，服务质量不断提升.那么前8个月保险业实现盈利( )
A.元B.元C.元D.元
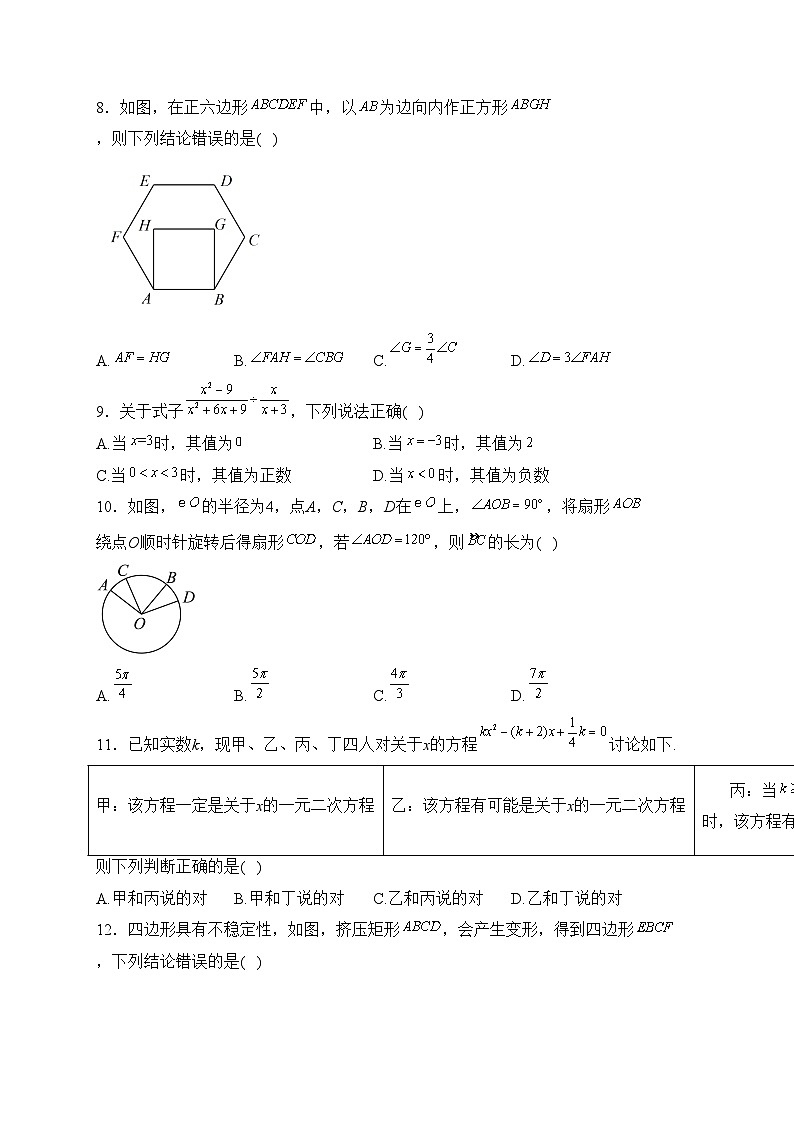
8．如图，在正六边形中，以为边向内作正方形，则下列结论错误的是( )
A.B.C.D.
9．关于式子，下列说法正确( )
A.当时，其值为B.当时，其值为
C.当时，其值为正数D.当时，其值为负数
10．如图，的半径为4，点A，C，B，D在上，，将扇形绕点O顺时针旋转后得扇形，若，则的长为( )
A.B.C.D.
11．已知实数k，现甲、乙、丙、丁四人对关于x的方程讨论如下.
则下列判断正确的是( )
A.甲和丙说的对B.甲和丁说的对C.乙和丙说的对D.乙和丁说的对
12．四边形具有不稳定性，如图，挤压矩形，会产生变形，得到四边形，下列结论错误的是( )
A.四边形是平行四边形B.四边形与矩形的面积相同
C.D.四边形与矩形的周长相同
13．如图，将三角形纸片沿虚线剪掉两角得五边形，若，，根据所标数据，则的度数为( )
A.B.C.D.
14．用一些完全相同的小正方体摆成一个几何体，如图是该几何体的左视图和俯视图，针对该几何体所需小正方体的个数m，三人的说法如下，
甲：若，则该几何体有两种摆法；
乙：若，则该几何体有三种摆法；
丙：若，则该几何体只有一种摆法.下列判断正确的是( )
A.甲对，乙错B.乙和丙都错C.甲错，乙对D.乙对，丙错
15．电影《刘三姐》中有这样一个对歌的场景.
该歌词表达的是一道数学题，其大意是：把300条狗分成4群，每个群里，狗的数量都是奇数，其中一个群，狗的数量少；另外三个群，狗的数量多且数量相同.问：应该如何分？设狗数量多的三个群均为x条，则正确的是( )
A.依题意狗数量少的群是条B.依题意
C.x有最小值，但无最大值D.是正确解，但不是唯一解
16．如图，等腰中，，D为边上一点.用尺规按如下的步骤操作：
①以点A为圆心，长为半径画弧，交的延长线于点E，连接；
②作的角平分线，交射线于点P，交于点Q.
结论Ⅰ：；结论Ⅱ：.
对于结论Ⅰ和Ⅱ，下列判断正确的是( )
A.Ⅰ不对Ⅱ对B.Ⅰ对Ⅱ不对C.Ⅰ和Ⅱ都对D.Ⅰ和Ⅱ都不对
二、填空题
17．如图，电路图上有3个开关和1个小灯泡.任意只闭合其中的1个开关，小灯泡发亮的概率是______.
18．一种燕尾夹如图1所示，图2是在闭合状态时的示意图（数据如图），则
（1）与是否平行？______（填“是”或“否”）；
（2）______.
19．如图，在中，点P在边上，点Q是的中点，反比例函数恰好经过P、Q两点.
（1）若点A坐标为，则______，点P坐标为______；
（2）若，则______.
三、解答题
20．如图，点A，B均在数轴上，点B在点A的右侧，点A对应的数字是，点B对应的数字是m.
（1）若，求m的值；
（2）将线段三等分，这两个等分点所对应数字从左到右依次是，，若，求m的取值范围.
21．设是一个两位数，其中a是十位上的数字（）.例如，当时，表示的两位数是45.
尝试：①当时，；②当时，；③当时，______；……
归纳：与有怎样的大小关系？
验证：请论证“归纳”中的结论正确.
22．某校甲、乙两名运动员连续8次射击训练成绩的折线统计图及统计表如下（统计图中乙的第8次成绩缺失）
甲、乙两人连续8次射击成绩统计表
（1）补全统计图和统计表；
（2）若规定7环及以上为优秀，试比较甲、乙两人谁的优秀率高；
（3）若甲再射击1次，命中7环，则甲的射击成绩的方差______（填“变大”“变小”或“不变”）.
23．某同学设计了一个动画，有两道光线：，：，其中m为常数，将第一象限区域设计为感光灯板.
（1）当光线经过点时，求出m的值，并指出点是否在光线上；
（2）若光线与的交点落在第一象限内，两光线可以聚焦使灯板发光.求此时整数m的取值个数.
24．如图，在半径为6的扇形中，点C，D在上，将沿弦折叠后恰好与，相切于点E，F，设所在的圆的圆心为，且.
（1）求的大小及的长；
（2）请在图中画出线段，用其长度表示劣弧上的点到弦的最大距离（不说理由），并求弦的长.
25．如图1，抛物线与x轴交于点，点，与y轴交于点C，顶点是D.
（1）求抛物线的解析式及顶点坐标D；
（2）如图1，点是线段上的动点（不与B，D重合），轴于F，设四边形的面积为S，求S与x之间的函数关系式，并求S的最大值；
（3）如图2，将抛物线向下平移k个单位长度，平移后的顶点为，与x轴的交点是，.若的外心在该三角形的内部，直接写出k的取值范围.
26．如图，在RtABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O逆时针旋转90°，交射线CB于点N.
（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；
（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；
（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且＜，请直接写出的值（用含k的式子表示）.
参考答案
1．答案：C
解析：
=
=
故选：C.
2．答案：B
解析：如图，过点P，点B的射线交于一点O，
故选：B.
3．答案：D
解析：A、当“□”为时，，故A选项不符合题意；
B、当“□”为0时，，故B选项不符合题意；
C、当“□”为时，，故C选项不符合题意；
D、当“□”为3时，，故D选项符合题意；
故选：D.
4．答案：B
解析：点A到的距离是三角形高线的长度，即线段是的高线，
故选B.
5．答案：D
解析：A.和不是最简同类二次根式，不能合并，所以A选项不符合题意；
B.，所以B选项不符合题意；
C.，所以C选项不符合题意；
D.，所以D选项符合题意.
故选：D.
6．答案：C
解析：两边都加上b得，，
等式可变形为，
，
.
故选：C.
7．答案：C
解析：，
故选C.
8．答案：D
解析：∵在正六边形和正方形中，
∴，，
∴，故A选项正确，不符合题意；
∵在正六边形和正方形中，
∴，，
∴，故B选项正确，不符合题意；
∵多边形是正六边形，
∴该多边形内角和为：，
∴，
∵多边形是正方形，
∴该多边形内角和为：，
∴，
∴，故C选项正确，不符合题意；
∵，
∴，故D选项不正确，符合题意
故选：D.
9．答案：A
解析：
，
A.当时，原式，故该说法正确，符合题意；
B.当时，分母，原式没有意义，不能计算求值，故该说法不正确，不符合题意；
C.当时，则，
∴，故该说法不正确，不符合题意；
D.当时，则，
∴，故该说法不正确，不符合题意.
故选：A.
10．答案：C
解析：∵，将扇形绕点O顺时针旋转后得扇形，，
∴，，
∴，
∵的半径为4，
∴，
故选：C.
11．答案：C
解析：当时，方程化为一元一次方程，解得；
故乙说的对；
当时，方程为一元二次方程，
当时，方程有两个实数根，此时且，
∴当时，方程有实数根，
故丙的说法正确.
综上可知，乙和丙说的对，
故选：C.
12．答案：B
解析：由图形挤压可知矩形会产生变形，但.
在矩形中：,
∴
∴四边形是平行四边形，故A选项正确，不符合题意；
∵拉成平行四边形后，高变小了，但底边大小没变
∴四边形比矩形的面积小了，故B选项不正确，符合题意；
∵四边形是平行四边形，
∴，
∵，
∴，
∴，故C选项正确，不符合题意；
∵四边形变成四边形的过程中每条边的长度没变，
∴周长没变，故D选项正确，不符合题意；
故选：B.
13．答案：B
解析：如图，
根据题意得：，，
∴，，
∵，，
∴，，
∴.
故选：B.
14．答案：C
解析：如图，
甲：若，则第一层已经摆放5个，第二层只放1个，由左视图的俯视图可得主视图如图①②③所示三种，故甲错；
乙：若，则第二层可放2个，可得主视图如④⑤⑥所示三种，故乙对；
丙：若，则第一层放5个，第二层放3个小正方体，这样只能摆放在后面三个小正方体上，主视图如图⑦所示，只有一种摆法，故丙对，
故选：C.
15．答案：D
解析：设狗数量多的三个群均为x条，
∵一个群，狗的数量少，三个群，狗的数量多且数量相同，狗的总数为300条，
∴狗的数量多的三个群的的总数为，狗数量少的群是条，故A选项错误，
∴，故B选项错误，
解得：，
∵，
∴，
∴，
∵为奇数且为整数，
∴有最小值，最大值为，
∴有最小值也有最大值，是正确解，但不是唯一解，故C选项错误，D选项正确，
故选：D.
16．答案：A
解析：∵是的角平分线，
∴，
∵D为边上一点，
∴不一定等于，
∴不一定等于，
∴Ⅰ不对；
∵是的角平分线，
∴，
∵，
∴，
又∵，
∴，
∴Ⅱ对.
故选：A.
17．答案：
解析：∵任意闭合一个开关，有三种等可能的结果，只闭合最上面的开关小灯泡才能发亮，
∴任意只闭合其中的1个开关，小灯泡发亮的概率为，
故答案为：.
18．答案：是；48
解析：（1）由图可得，
∴，
故答案为：是；
（2）∵，
∴，
∴，
∴，
解得，
故答案为：48.
19．答案：6；；
解析：（1），，点Q是的中点，
点的坐标为，
反比例函数经过点Q，
，
轴，点P在边上，
点P的横坐标为6，
反比例函数经过点P，
，
点P坐标为，
故答案为：6；；
（2）设，
，点Q是的中点，
点的坐标为，
反比例函数经过点Q，
，
轴，点P在边上，
点P的横坐标为，
反比例函数经过点P，
，
点P坐标为，
，
，
，
，
，
故答案为：.
20．答案：（1）
（2）
解析：（1）∵，
∴，
即m的值为；
（2）∵，
∴，
∴，
∵，
∴，解得.
21．答案：尝试
归纳
验证：见解析
解析：尝试：当时，；
归纳：；
验证：等号左边，
等号右边，
所以，等号左边＝等号右边，等式成立，即证.
22．答案：（1）见解析，7，8，6
（2）甲的优秀率高
（3）变小
解析：（1）乙的第8次射击的环数为（环），
将乙的8次射击成绩从小到大排列为3，4，5，6，6，7，8，9，
乙的中位数为（环），
甲的平均数为（环），
甲的众数为8，
补全图表如下：
（2）甲命中7环及以上的次数为5次，优秀率为，
乙命中7环及以上的次数为3次，优秀率为，
，
甲的优秀率高；
（3）甲再射击1次，命中7环，
甲的平均数还是7环，
甲的方差为，
甲的方差变小，
故答案为：变小.
23．答案：（1）；点在光线上
（2）5或6，共2个
解析：（1）把，代入得，，
解得；
∴的表达式为，当时，，
∴点在光线上；
（2）联立解析式得，解得，
∴光线与的交点坐标为，
∵交点在第一象限，
∴，解得，
∴整数m的值为5或6，共2个.
24．答案：（1），
（2）见解析；
解析：（1）如图所示，连接、、OD，
由对称性可知，
即，
∵与，相切于点E，F，
∴，，
∴，，
在四边形中，；
∵，，
∴平分，
即，
在中，；
（2）如图中的即为所求，
作法：过O作交于P，延长与交于点Q，
理由：由折叠可知：垂直平分，
∴ 是所在弓形的高，
即的长度是劣弧上的点到弦的最大距离，
则O、、P三点共线，
在中，，
由对称性可知，
在中，，
所以.
25．答案：（1），
（2），
（3）
解析：（1）把，和，代入
可得，解得，
故抛物线解析式为，，
故D的坐标为；
（2）由抛物线解析式可得，设所在直线的解析式为，
把，和，代入
可得，解得，
∴，
∴设.
由于四边形为梯形，
∴，
∵，
∴当时，S有最大值为.
（3）由题意得，为锐角三角形，
设平移后的抛物线解析式为，
当为直角三角形时，
根据抛物线对称性可知，为等腰直角三角形，
∵，
∴，，
将或代入
得或（三点重合，舍去），
∴.
26．答案：（1）OM＝ON，见解析
（2）ON＝k•OM，见解析
（3）
解析：（1）OM＝ON，如图1，
作OD⊥AM于D，OE⊥CB于E，
∴∠ADO＝∠MDO＝∠CEO＝∠OEN＝90°，
∴∠DOE＝90°，
∵AC＝BC，∠ACB＝90°，
∴∠A＝∠ABC＝45°，
在Rt△AOD中，
，
同理：OE＝OB，
∵OA＝OB，
∴OD＝OE，
∵∠DOE＝90°，
∴∠DOM＋∠MOE＝90°，
∵∠MON＝90°，
∴∠EON＋∠MOE＝90°，
∴∠DOM＝∠EON，
在Rt△DOM和Rt△EON中，
，
∴△DOM≌△EON（ASA），
∴OM＝ON.
（2）如图2，
作OD⊥AM于D，OE⊥BC于E，
由（1）知：OD＝OA，OE＝OB，
∴，
由（1）知：
∠DOM＝∠EON，∠MDO＝∠NEO＝90°，
∴△DOM∽△EON，
∴，
∴ON＝k•OM.
（3）如图3，
设AC＝BC＝a，
∴AB＝a，
∵OB＝k•OA，
∴OB＝•a，OA＝•a，
∴OE＝OB＝a，
∵∠N＝∠ABC﹣∠BON＝45°﹣15°＝30°，
∴EN＝＝OE＝•a，
∵CE＝OD＝OA＝a，
∴NC＝CE＋EN＝a＋•a，
由（2）知：，△DOM∽△EON，
∴∠AMO＝∠N＝30°
∵，
∴，
∴△PON∽△AOM，
∴∠P＝∠A＝45°，
∴PE＝OE＝a，
∴PN＝PE＋EN＝a＋•a，
设AD＝OD＝x，
∴DM＝，
由AD＋DM＝AC＋CM得，
（＋1）x＝AC＋CM，
∴x＝（AC＋CM）＜（AC＋AC）＝AC，
∴k＞1
∴，


∴.
甲：该方程一定是关于x的一元二次方程
乙：该方程有可能是关于x的一元二次方程
丙：当时，该方程有实数根
丁：只有当且时，该方程有实数根
罗秀才：三百条狗交给你，一少三多四下分，不要双数要单数，看你怎样分得匀？
刘三姐的姐妹们：九十九条打猎去，九十九条看羊来，九十九条守门口，剩下三条给财主.
平均数
中位数
众数
方差
甲
______
______
乙
6
______
6
平均数
中位数
众数
方差
甲
7
8
乙
6
6
6