中考数学专题复习线段、角、相交线与平行线

这是一份中考数学专题复习线段、角、相交线与平行线，共4页。


1. 如图，直线a∥b，直线c分别与a，b相交，∠1＝50°，则∠2的度数为( )
A．150° B．130° C．100° D．50°
2. 如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为( )
A．40° B．50° C．60° D．70°
3. 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，则点P到BC的距离是( )
A．8 B．6 C．4 D．2
4. 能说明命题“对于任何实数a，|a|＞ －a”是假命题的一个反例可以是( )
A．a＝－2 B．a＝eq \f(1,3) C．a＝1 D．a＝eq \r(2)
5. 已知AD∥BC，AB⊥AD，点E，点F分别在射线AD，射线BC上，若点E与点B关于AC对称，点E与点F关于BD对称，AC与BD相交于点G.则( )
A．1＋tan∠ADB＝eq \r(2) B．2BC＝5CF
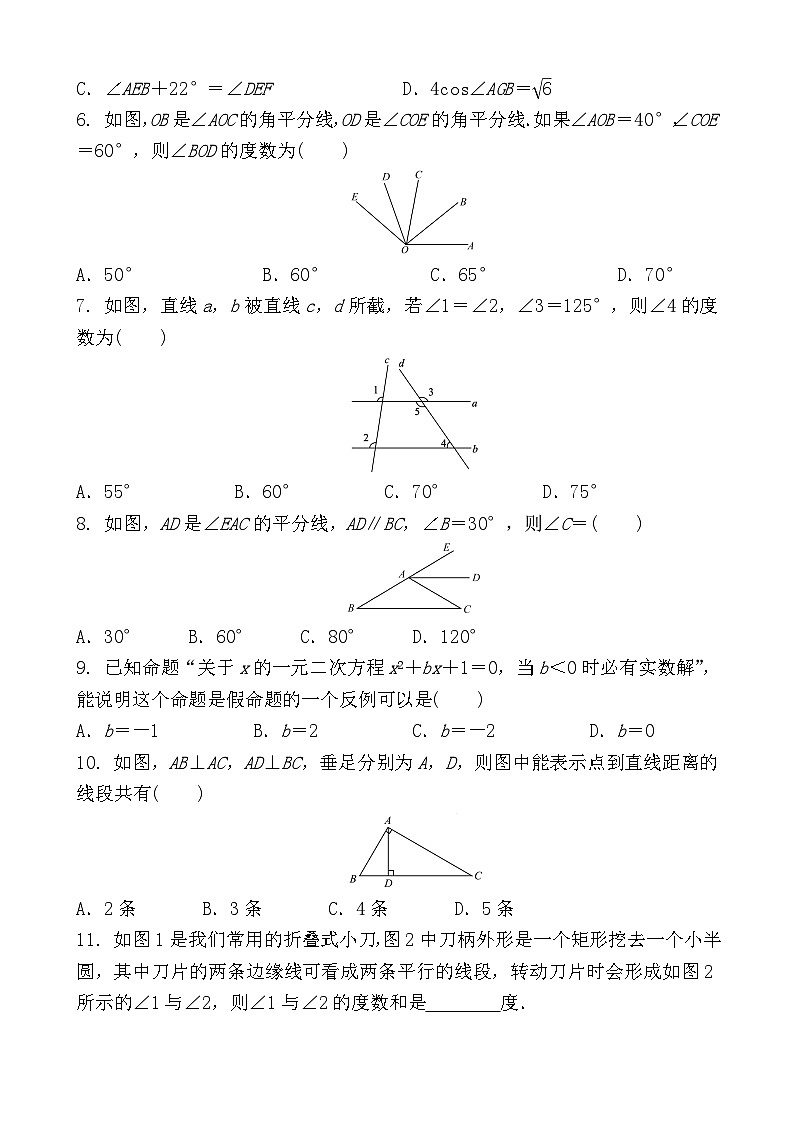
C．∠AEB＋22°＝∠DEF D．4cs∠AGB＝eq \r(6)
6. 如图，OB是∠AOC的角平分线，OD是∠COE的角平分线．如果∠AOB＝40°，∠COE＝60°，则∠BOD的度数为( )
A．50° B．60° C．65° D．70°
7. 如图，直线a，b被直线c，d所截，若∠1＝∠2，∠3＝125°，则∠4的度数为( )
A．55° B．60° C．70° D．75°
8. 如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C＝( )
A．30° B．60° C．80° D．120°
9. 已知命题“关于x的一元二次方程x2＋bx＋1＝0，当b＜0时必有实数解”，能说明这个命题是假命题的一个反例可以是( )
A．b＝－1 B．b＝2 C．b＝－2 D．b＝0
10. 如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有( )
A．2条 B．3条 C．4条 D．5条
11. 如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是 度．

12. 如图，点A，C，F，B在同一直线上，CD平分∠ECB，FG∥CD，若∠ECA为α度，则∠GFB为 度(用关于α的代数式表示)．
13. 如图折叠一张矩形纸片，已知∠1＝70°，则∠2的度数是_________．
14. 如图，已知直线AB，CD相交于点O，OE，OF为射线，∠AOE＝90°，OF平分∠AOC，∠AOF＋∠BOD＝51°，求∠EOD的度数．
参考答案：
1---10 BBCAA DAAAD
11. 90
12. eq \b\lc\(\rc\)(\a\vs4\al\c1(90－\f(α,2)))
13. 55°
14. 解：∵∠AOC＝∠BOD，OF平分∠AOC，
∴∠AOF＝eq \f(1,2)∠AOC＝eq \f(1,2)∠BOD．
∵∠AOF＋∠BOD＝51°，
∴∠AOF＝17°，∠BOD＝34°.
∵∠AOE＝90°，
∴∠BOE＝180°－∠AOE＝90°，
∴∠EOD＝90°＋34°＝124°.