江苏省泰州市靖江市 八校联盟阶段测试2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版）

这是一份江苏省泰州市靖江市 八校联盟阶段测试2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版），文件包含精品解析江苏省泰州市靖江市八校联盟阶段测试2023-2024学年七年级下学期3月月考数学试题原卷版docx、精品解析江苏省泰州市靖江市八校联盟阶段测试2023-2024学年七年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
（考试时间：100分钟满分：100分）
一、选择题（每题2分）
1. 计算的结果是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据同底数幂乘法运算法则进行计算即可．
【详解】解：，
故选：B．
【点睛】本题主要考查了同底数幂的乘法，解题的关键是掌握同底数幂相乘，底数不变，指数相加．
2. 若一个三角形三个内角度数的比为2：3：4，那么这个三角形是（ ）
A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形
【答案】B
【解析】
【分析】将三个内角分别设为2k、3k、4k，利用三角形内角和即可求出三个角的度数，然后即可判断三角形的形状．
【详解】解：∵三角形三个内角度数比为2：3：4，
设三个内角分别为2k、3k、4k，
由题意得，2k+3k+4k＝180，
解得k＝20，
∴三个内角分别为40°、60°、80°，
∴这个三角形是锐角三角形．
故选：B．
【点睛】此题考查的是判断三角形的形状，掌握三角形的内角和定理和三角形的分类是解决此题的关键．
3. 有长为的四根木棒，选其中的3根作为三角形的边，可以围成的三角形的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】本题考查的是三角形的三边关系，即三角形任意两边之和大于第三边，任意两边之差小于第三边．先写出不同的分组，再根据三角形的任意两边之和大于第三边，任意两边之差小于第三边对各组数据进行判断即可得解．
【详解】解：任取3根可以有以下几组：
①，能够组成三角形；
②，
∵，
∴不能组成三角形；
③，能组成三角形；
④，能组成三角形；
∴可以搭出不同的三角形3个．
故选：C．
4. 已知等腰三角形的两条边长分别是7和3，则第三条边的长可能为（ ）
A. 8B. 7C. 4D. 3
【答案】B
【解析】
【分析】因为腰长与底边不确定，所以分①7为腰长，3为底边，②7为底边，3为腰长两种情况，再根据“三角形任意两边之和大于第三边，两边之差小于第三边”进行讨论.
【详解】解：分两种情况讨论：
①当7为腰长，3为底边时，三边为7、7、3，能组成三角形，故第三边的长为7，
②当3为腰长，7为底边时，三边为7、3、3，3+3=6＜7，所以不能组成三角形．
∴第三边的长为7．
故选B．
【点睛】此题主要考查等腰三角形的性质及三角形三边关系的运用；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
5. 如图，已知，平分交于D点，，则为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查平行线的性质，角平分线的性质，三角形的内角和定理，根据平行加角平分线得到，邻补角求出的度数，三角形的内角和求出即可．
【详解】解：∵，
∴，
∵平分，
∴，
∴，
∵，
∴，
∴；
故选A．
6. 小明同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2005°，则n等于 ( )
A. 11B. 12C. 13D. 14
【答案】D
【解析】
【详解】解：设少输入的这个内角的度数是x，根据三角形的内角和公式得：
，
，
因为n是正整数，0°＜x＜180°，所以当x=155°时，n=14．
故选D．
二、填空题（每题2分）
7. 计算______．
【答案】
【解析】
【分析】根据幂的乘方法则求解即可．
【详解】解：．
故答案为：．
【点睛】本题考查了幂的运算法则，掌握幂的乘方法则是解本题的关键．
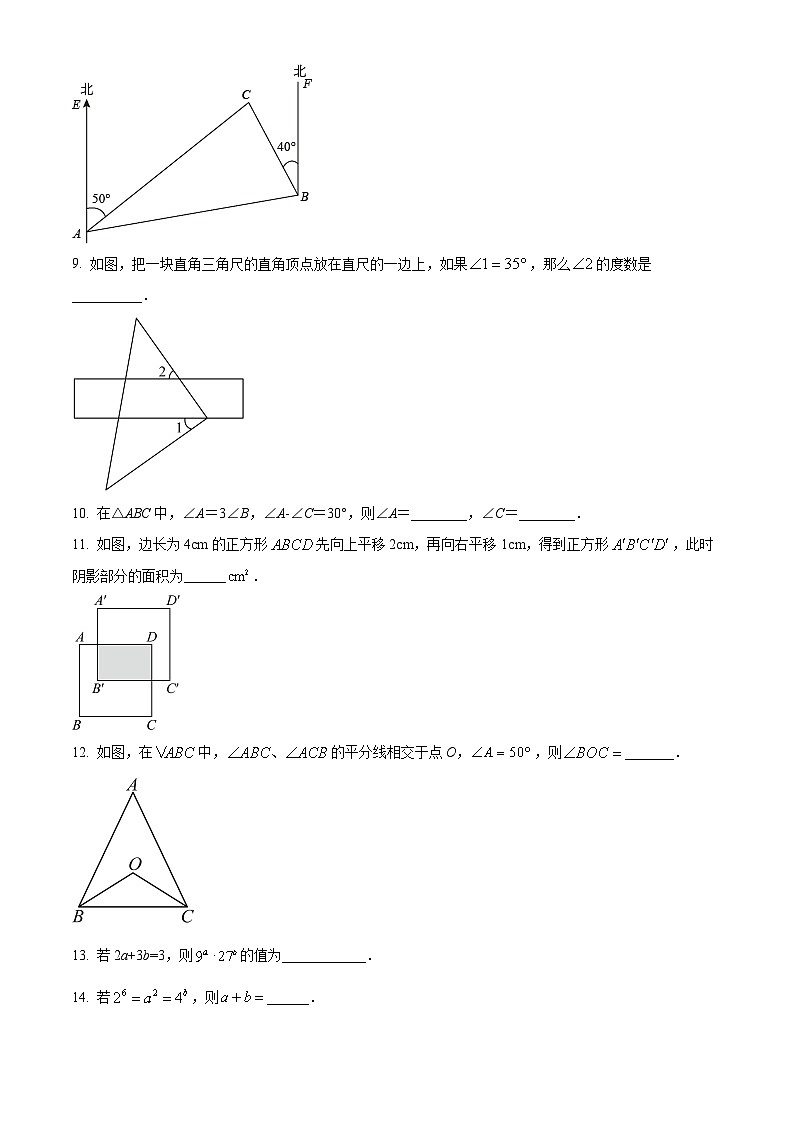
8. 如图所示，C岛在A岛北偏东50°方向，C岛在B岛的北偏西40°方向，则从C岛看A、B两岛的视角∠ACB等于________．
【答案】90°
【解析】
【分析】根据方位角的概念和平行线的性质即可得答案．
【详解】过点C作CD∥AE，
∵AE∥BF，
∴CD∥AE∥BF，
∴∠ACD＝∠EAC＝50°，∠BCD＝∠CBF＝40°，
∴∠ACB＝∠ACD十∠BCD＝50°+40°＝90°．
故答案为90．
【点睛】本题考查方位角的概念及平行线的性质，解答此类题需要从运动的角度，结合平行线的性质求解．
9. 如图，把一块直角三角尺的直角顶点放在直尺的一边上，如果，那么的度数是__________．
【答案】55°
【解析】
【分析】如图，利用平行线的性质得到∠2＝∠3，然后利用互余计算∠2的度数．
【详解】解：如图，
∵a∥b，
∴∠2＝∠3，
∵∠1+∠3＝90°，∠1＝35°，
∴∠2＝∠3＝90°﹣35°＝55°．
故答案为：55°．
【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
10. 在△ABC中，∠A＝3∠B，∠A-∠C＝30°，则∠A＝________，∠C＝________．
【答案】 ①. 90°##90度 ②. 60°##60度
【解析】
【分析】根据三角形内角和得到∠A+∠B+∠C＝180°，∠A＝3∠B，∠A-∠C＝30°，把两式相加消去∠B即可求得∠A的度数．
【详解】解：∵∠A+∠B+∠C＝180°，∠A＝3∠B，∠A-∠C＝30°，
则
∴∠A+∠A+∠A＝180°，
∴∠A＝90°，．
故答案为90°,60°．
【点睛】本题考查了三角形内角和定理：三角形内角和是180°．主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．
11. 如图，边长为4cm的正方形先向上平移2cm，再向右平移1cm，得到正方形，此时阴影部分的面积为______．

【答案】6
【解析】
【分析】根据题意和平移的特点，可以写出和的长度，然后即可计算出阴影部分的面积．
【详解】解：如图，

由题意可得，，
∴阴影部分的面积：，
故答案为：6．
【点睛】本题考查正方形的性质、平移的性质，解答本题的关键是明确题意，求出和的长度．
12. 如图，在中，的平分线相交于点O，，则_______．
【答案】115°##115度
【解析】
【分析】本题考查与角平分线有关的三角形的内角和问题，根据三角形内角和定理求出的度数，角平分线得到，再根据三角形的内角和定理进行求解即可。
【详解】解：∵在中，，
∴，
∵的平分线相交于点O，
∴，
∴；
故答案为：
13. 若2a+3b=3，则·的值为____________．
【答案】27
【解析】
【分析】根据幂的乘方及同底数幂的乘法将原式变形求值即可．
【详解】解：
∵2a+3b=3
∴原式=，
故答案为：27．
【点睛】题目主要考查幂的乘方及同底数幂的乘法，求代数式的值，熟练掌握运用幂的乘方及同底数幂的乘法是解题关键．
14 若，则______．
【答案】或## 或
【解析】
【分析】根据，求出，，代入计算即可．
【详解】解析：由，可得，，则或．
故答案为：或
【点睛】本题考查乘方的逆运算，平方根，解题的关键是求出，．
15. 已知a，b，c是一个三角形的三条边长，则化简_______．
【答案】0
【解析】
【分析】本题考查绝对值的性质，整式的加减，三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．根据三角形三边关系得到，，再去绝对值，合并同类项即可求解．
【详解】解：∵a，b，c是一个三角形的三条边长，
∴，，
∴
．
故答案为：0．
16. 如图，是的平分线，是的平分线，与交于G，若，，则为__________．

【答案】##80度
【解析】
【分析】本题主要考查了三角形内角和的应用，首先连接，根据三角形的内角和定理，求出，∠1+∠2+∠3+∠4=70°；然后判断出，再根据是的平分线，是的平分线，判断出；最后根据三角形的内角和定理，用即可求出∠A的度数．
【详解】解：如图所示，连接，

∵，
∴，
∵，
∴，
∴，
∵是的平分线，是的平分线，
∴∠3=∠5，∠4=∠6，
又∵，
∴，
∴，
∴．
故答案为：．
三、解答题：
17 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题考查幂的运算，合并同类项：
（1）先进行积的乘方，幂的乘方运算，再进行单项式乘单项式的运算，最后合并同类项即可；
（2）先进行积的乘方，幂的乘方运算，再进行单项式乘单项式的运算，最后合并同类项即可．
【小问1详解】
解：原式
；
【小问2详解】
原式
．
18. 如图，为的中线，为的中线．
（1）若，则 °；
（2）在中作边上的高（保留必要的作图痕迹）；
（3）若的面积为，，则点E到边的距离 ．
【答案】（1）75 （2）图见解析
（3）2
【解析】
【分析】本题考查三角形的外角，三角形的高线和中线：
（1）利用三角形外角的性质，求解即可；
（2）根据三角形的高线的定义，画出即可；
（3）设点E到边的距离为，根据三角形的中线平分面积结合三角形的面积公式进行求解即可．
【小问1详解】
解：∵，是的一个外角，
∴；
故答案为：75；
【小问2详解】
如图，高即为所求；
【小问3详解】
∵的面积为，为的中线，
∴，
∵为的中线，
∴，
设点E到边的距离为，
∴，
∵，
∴；
故答案为：2．
19. 已知：如图，，，求证：．
【答案】见解析
【解析】
【分析】根据，可得，根据平行线的性质可得，根据已知可得，等量代换即可得证．
【详解】证明：∵，
∴，
∴，
∵，
∴
∴．
【点睛】本题考查了平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．
20. ①若，求的值．
②已知，，求的值．
【答案】①14；②1．
【解析】
【分析】本题考查了积的乘方与幂的乘方，熟练掌握幂的混合运算是解题的关键．
①根据积的乘方与幂的乘方，进行计算即可求解；②根据积的乘方与幂的乘方，进行计算即可求解；
【详解】解：①
=，
当时，原式=；
②
=
=
=，
当，时，原式=，
∵为偶数，
∴原式=1．
21. 请将下列证明过程补充完整：
如图，点E、F、M、N分别在线段、、上，，，
求证：．

证明：∵（已知）
∴ （同位角相等，两直线平行）
∴（ ）
∵（已知）
又∵（ ）
∴（ ）
∴（ ）
∴（同位角相等，两直线平行）
∴（ ）．
【答案】；两直线平行，内错角相等；邻补角的性质；同角的补角相等；等量代换；两直线平行，同位角相等；
【解析】
【分析】本题考查的是平行线的判定与性质，邻补角的性质，根据题干的提示逐一完善推理过程与推理依据即可，掌握平行线的判定方法与性质是解本题的关键．
【详解】证明：∵（已知）
∴（同位角相等，两直线平行）
∴（两直线平行，内错角相等）
∵（已知）
又∵（邻补角的性质）
∴（同角的补角相等）
∴（等量代换）
∴（同位角相等，两直线平行）
∴（两直线平行，同位角相等）．
22. 如图，在△ABC中，∠B=30°，∠C=50°，AE是∠BAC的平分线，AD是高．
（1）求∠BAE的度数；
（2）求∠EAD的度数．
【答案】（1）50°；（2）10°．
【解析】
【详解】（1）根据△ABC的内角和定理求得∠BAC=100°；然后由角平分线的性质、△ABE的内角和定理来求∠BAE的度数；（2）由三角形内角和定理可求得∠BAC的度数，在Rt△ADC中，可求得∠DAC的度数，AE是角平分线，有∠EAC=∠BAC，故∠EAD=∠EAC-∠DAC．
解：（1）∵在△ABC中，∠B=30°，∠C=50°，
∴∠BAC=180°﹣∠B﹣∠C=100°；
又∵AE是∠BAC的平分线，
∴∠BAE=∠BAC=50°；
（2）∵AD是边BC上高，∴∠ADC=90°，
∴在△ADC中，∠C=50°，∠C+∠DAC=90°，
∴∠DAC=40°，
由（1）知，∠BAE=∠CAE=50°，
∴∠DAE=∠EAC﹣∠DAC=50°﹣40°=10°，即∠EAD=10°．
23. 如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,问:CE与DF的位置关系怎样?试说明理由.
【答案】CE∥DF.理由见解析.
【解析】
【分析】根据BD平分∠ABC，CE平分∠ACB，得出∠DBF=∠ABC，∠ECB=∠ACB，∠DBF=∠ECB，再根据∠DBF=∠F，得出∠ECB=∠F，即可证出EC∥DF．
【详解】EC//DF，理由如下：
∵BD平分∠ABC，CE平分∠ACB，
∴∠DBF=∠ABC，∠ECB=∠ACB，
∵∠ABC=∠ACB，
∴∠DBF=∠ECB，
∵∠DBF=∠F，
∴∠ECB=∠F，
∴EC∥DF．
【点睛】本题主要考查了平行线的判定，用到的知识点是同位角相等，两直线平行，证明得出∠ECB=∠F是解题关键.
24. 如图，已知，，平分，试说明．
【答案】证明见解析
【解析】
【分析】本题考查的是平行线的判定与性质的应用，关键在于利用平行线的性质及判定定理将角进行转化，从而证明出两个角相等． 先证明，可得，再证明，可得，证明，结合平分，可得，从而可得结论．
【详解】证明：∵，，
∴，
∴，
∴，
又∵，
∴，
∴，
∴，，
∴，
又∵平分，
∴，
∴．
25. 如图，直线EF∥GH，点B、A分别在直线EF、GH上，连接AB，在AB左侧作三角形ABC，其中∠ACB＝90°，且∠DAB＝∠BAC，直线BD平分∠FBC交直线GH于D
(1) 若点C恰在EF上，如图1，则∠DBA＝_________
(2) 将A点向左移动，其它条件不变，如图2，则（1）中的结论还成立吗？若成立，证明你的结论；若不成立，说明你的理由
(3) 若将题目条件“∠ACB＝90°”，改为：“∠ACB＝120°”，其它条件不变，那么∠DBA＝_________（直接写出结果，不必证明）

【答案】(1)45°;(2)见解析;(3)60°.
【解析】
【分析】（1）根据两直线平行，同旁内角互补求出∠CAD=90°，然后求出∠BAC=45°，从而得到∠ABC=45°，再根据BD平分∠FBC求出∠DBC=90°，然后求解即可；
（2）根据两直线平行，内错角相等可得∠2=∠3，再根据三角形的内角和定理表示出∠4，然后表示∠5，再利用平角等于180°列式表示出∠DBA整理即可得解；
（3）根据（2）的结论计算即可得解．
【详解】解：（1）∵EF∥GH，
∴∠CAD=180°-∠ACB=180°-90°=90°，
∵∠DAB=∠BAC，
∴∠BAC=45°，
∴∠ABC=45°，
∵BD平分∠FBC，
∴∠DBC=×180°=90°，
∴∠DBA=90°-45°=45°；
（2）解：如图，设∠DAB=∠BAC=x，即∠1=∠2=x，
∵EF∥GH，
∴∠2=∠3，
在△ABC内，∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x，
∵直线BD平分∠FBC，
∴∠5=（180°-∠4）=（180°-180°+∠ACB+2x）=∠ACB+x，
∴∠DBA=180°-∠3-∠4-∠5，
=180°-x-（180°-∠ACB-2x）-（∠ACB+x），
=180°-x-180°+∠ACB+2x-∠ACB-x，
=∠ACB，
=×90°，
=45°；

（3）由（2）可知，∠ACB=120°时，
∠DBA=×120°=60°．
【点睛】本题考查了平行线的性质，角平分线的定义，三角形的内角和定理，熟记性质并理清图中各角度之间的关系是解题的关键．