中考数学二轮重难点复习讲义模型17 阿氏圆最值问题（2份打包，原卷版+解析版）

这是一份中考数学二轮重难点复习讲义模型17 阿氏圆最值问题（2份打包，原卷版+解析版），文件包含中考数学二轮重难点复习讲义模型17阿氏圆最值问题原卷版doc、中考数学二轮重难点复习讲义模型17阿氏圆最值问题解析版doc等2份试卷配套教学资源，其中试卷共51页， 欢迎下载使用。

背景故事：“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A、B两点，点P满足PA：PB=k（k≠1），则满足条件的所有的点P的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.
模型建立：当点P在一个以O为圆心，r为半径的圆上运动时，如图所示：
易证：△BOP∽△POA， SKIPIF 1 < 0 ，∴对于圆上任意一点P都有 SKIPIF 1 < 0 .
对于任意一个圆，任意一个k的值，我们可以在任意一条直径所在直线上，在同侧适当的位置选取A、B点，则需 SKIPIF 1 < 0
【技巧总结】计算 SKIPIF 1 < 0 的最小值时，利用两边成比例且夹角相等构造母子型相似三角形
问题：在圆上找一点P使得 SKIPIF 1 < 0 的值最小，解决步骤具体如下：
①如图，将系数不为1的线段两端点与圆心相连即OP，OB
②计算出这两条线段的长度比 SKIPIF 1 < 0
③在OB上取一点C，使得 SKIPIF 1 < 0 ，即构造△POM∽△BOP，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0
④则 SKIPIF 1 < 0 ，当A、P、C三点共线时可得最小值
例题精讲
【例1】．如图，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P为圆上一动点，连接AP，BP，则AP+BP的最小值为________.
变式训练
【变式1-1】．如图，正方形ABCD的边长为4，⊙B的半径为2，P为⊙B上的动点，则PD+PC的最小值等于 ．
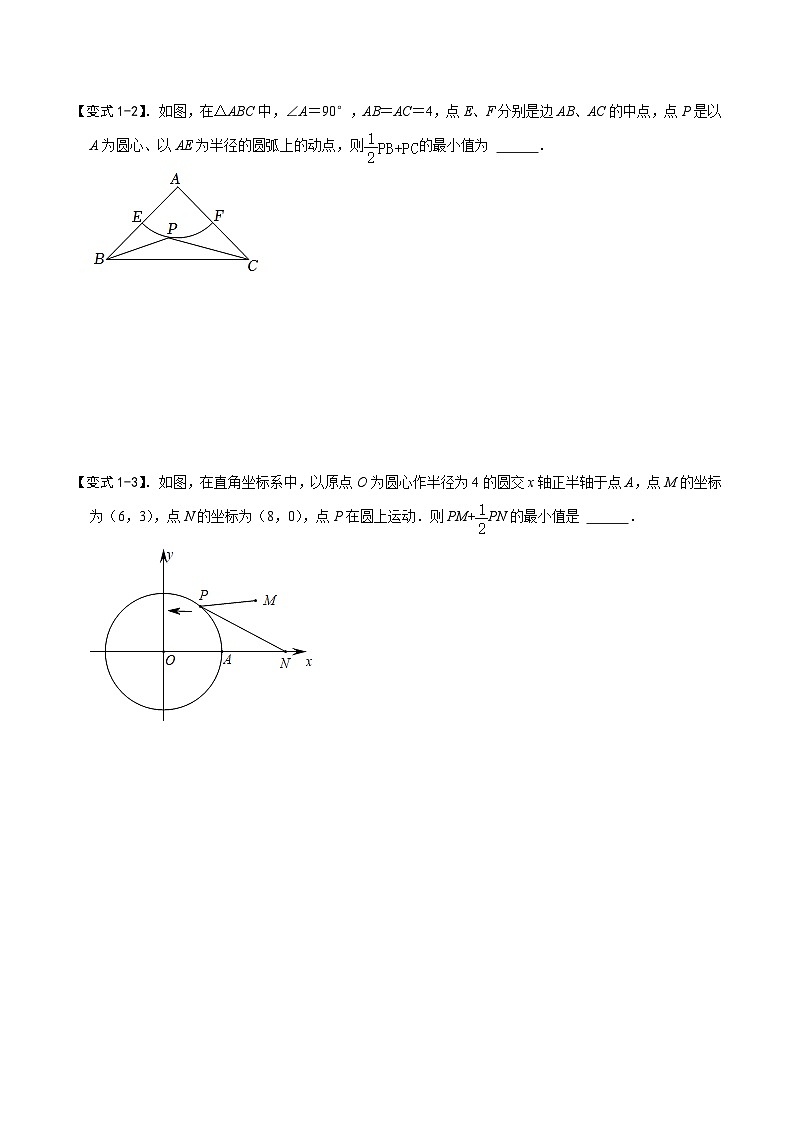
【变式1-2】．如图，在△ABC中，∠A＝90°，AB＝AC＝4，点E、F分别是边AB、AC的中点，点P是以A为圆心、以AE为半径的圆弧上的动点，则的最小值为 ．
【变式1-3】．如图，在直角坐标系中，以原点O为圆心作半径为4的圆交x轴正半轴于点A，点M的坐标为（6，3），点N的坐标为（8，0），点P在圆上运动．则PM+PN的最小值是 ．
【例2】．如图，在⊙O中，点A、点B在⊙O上，∠AOB＝90°，OA＝6，点C在OA上，且OC＝2AC，点D是OB的中点，点M是劣弧AB上的动点，则CM+2DM的最小值为 ．
变式训练
【变式2-1】．⊙O半径为2，AB，DE为两条直线．作DC⊥AB于C，且C为AO中点，P为圆上一个动点．求2PC+PE的最小值．
【变式2-2】．如图，在扇形OCD中，∠COD＝90°，OC＝3，点A在OD上，AD＝1，点B为OC的中点，点E是弧CD上的动点，则AE+2EB的最小值是 ．
【变式2-3】．如图，等边△ABC的边长6，内切圆记为⊙O，P是⊙O上一动点，则2PB+PC的最小值为 ．

1．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则PA+PB的最小值为 ．
2．如图，扇形AOB中，∠AOB＝90°，OA＝6，C是OA的中点，D是OB上一点，OD＝5，P是上一动点，则PC+PD的最小值为 ．
3．如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，P为弧AB上一动点，则PC+PD的最小值为 ．

4．在Rt△AOB中，∠AOB＝90°，OA＝8，OB＝10，以O为圆心，4为半径作圆O，交两边于点C，D，P为劣弧CD上一动点，则PA+PB最小值为 ．
5．如图，在边长为6的正方形ABCD中，M为AB上一点，且BM＝2，N为边BC上一动点，连接MN，点B关于MN对称，对应点为P，连接PA，PC，则PA+2PC的最小值为 ．
6．如图，矩形ABCD中，AB＝2，AD＝4，M点是BC的中点，A为圆心，AB为半径的圆交AD于点E．点P在上运动，则PM+DP的最小值为 ．
7．如图，在△ABC中，∠A＝90°，AB＝3，AC＝4，D为AC的中点，以A为圆心，AD为半径作OA交AB于点E，P为劣弧DE上一动点，连接PB、PC，则PC+PB的最小值为 ．
8．如图，在平面直角坐标系中，A（2，0）、B（0，2）、C（4，0）、D（3，2），P是△AOB外部的第一象限内一动点，且∠BPA＝135°，则2PD+PC的最小值是 ．
9．如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝2，⊙O的半径为1，M为⊙O上一动点，求AM+BM的最小值．
10．问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连接AP，BP，求AP+BP的最小值．
（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，
∴＝，∴PD＝BP，∴AP+BP＝AP+PD．
请你完成余下的思考，并直接写出答案：AP+BP的最小值为 ．
（2）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形内部一点，且PB＝3，AP+PC的最小值为 ．
（3）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P是上一点，求2PA+PB的最小值，画出示意图并写出求解过程．
11．（1）如图1，已知正方形ABCD的边长为6，圆B的半径为3，点P是圆B上的一个动点，则PD+PC的最小值为 ，PD﹣PC的最大值为 ．
（2）如图2，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，求PD+PC的最小值，以及PD﹣PC的最大值．
12．阅读以下材料，并按要求完成相应的任务．
已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．
阿氏圆基本解法：构造三角形相似．
【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．
阿氏圆的关键解题步骤：
第一步：如图1，在OD上取点M，使得OM：OP＝OP：OD＝k；
第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．
下面是该题的解答过程（部分）：
解：在OD上取点M，使得OM：OP＝OP：OD＝k，
又∵∠POD＝∠MOP，∴△POM∽△DOP．
任务：
（1）将以上解答过程补充完整．
（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．
13．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+的最小值和PD﹣的最大值；
（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为 ，PD﹣的最大值为 ．
（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD+的最小值为 ，PD﹣的最大值为 ．
14．如图，抛物线y＝﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y＝﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．
（1）求抛物线y＝﹣x2+bx+c的表达式；
（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；
（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；
②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．
15．如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B（8，0）．
（1）求二次函数的表达式；
（2）求顶点A的坐标及直线AB的表达式；
（3）判断△ABO的形状，试说明理由；
（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E的运动时间t的最小值．