


所属成套资源:中考数学二轮重难点复习讲义(2份打包,原卷版+解析版)
中考数学二轮重难点复习讲义模型05 相似三角形中的常见五种基本模型(2份打包,原卷版+解析版)
展开
这是一份中考数学二轮重难点复习讲义模型05 相似三角形中的常见五种基本模型(2份打包,原卷版+解析版),文件包含中考数学二轮重难点复习讲义模型05相似三角形中的常见五种基本模型原卷版doc、中考数学二轮重难点复习讲义模型05相似三角形中的常见五种基本模型解析版doc等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
相似三角形考查范围广,综合性强,其模型种类多,其中有关一线三垂直模型在前面的专题已经很详细的讲解,这里就不在重复.
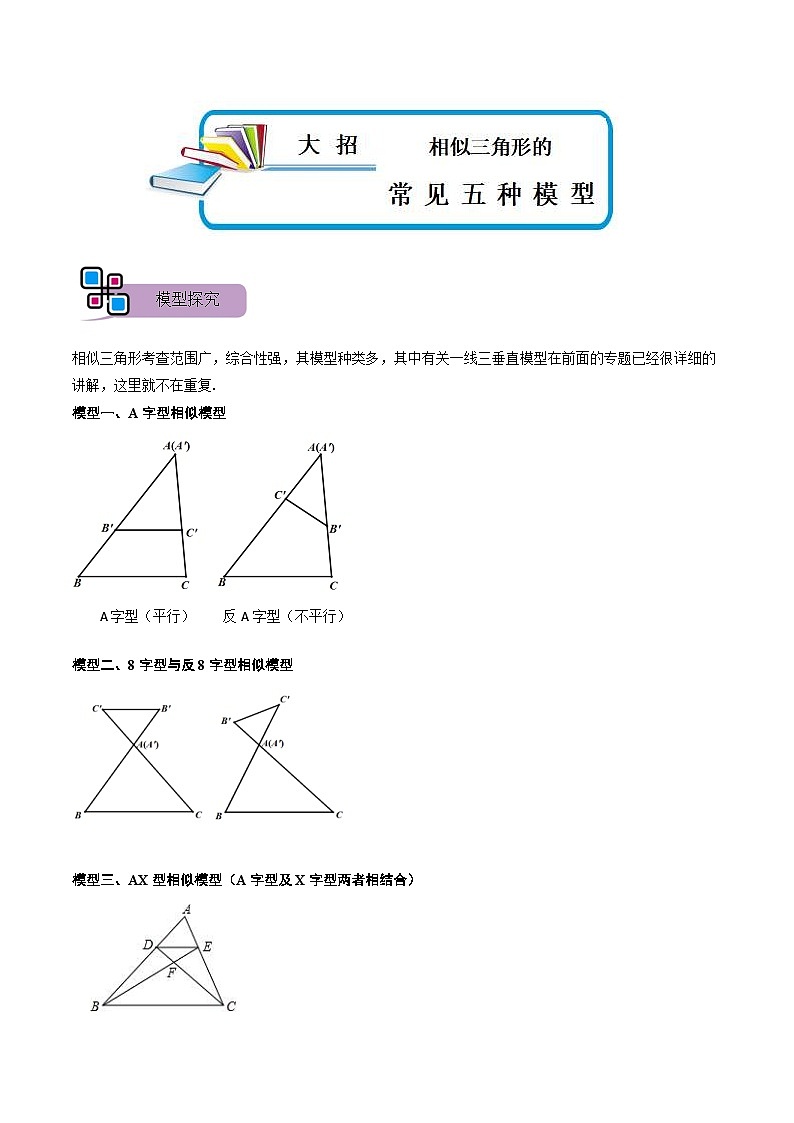
模型一、A字型相似模型
A字型(平行) 反A字型(不平行)
模型二、8字型与反8字型相似模型
模型三、AX型相似模型(A字型及X字型两者相结合)
模型四、共边角相似模型(子母型)
模型五、手拉手相似模型
例题精讲
考点一、A字相似模型
【例1】.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A.B.
C.D.
解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;
C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;
故选:C.
变式训练
【变式1-1】.如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若,则= .
解:∵,
∴,
∵DE∥BC,
∴△ADE∽△ABC,
∴,故答案为.
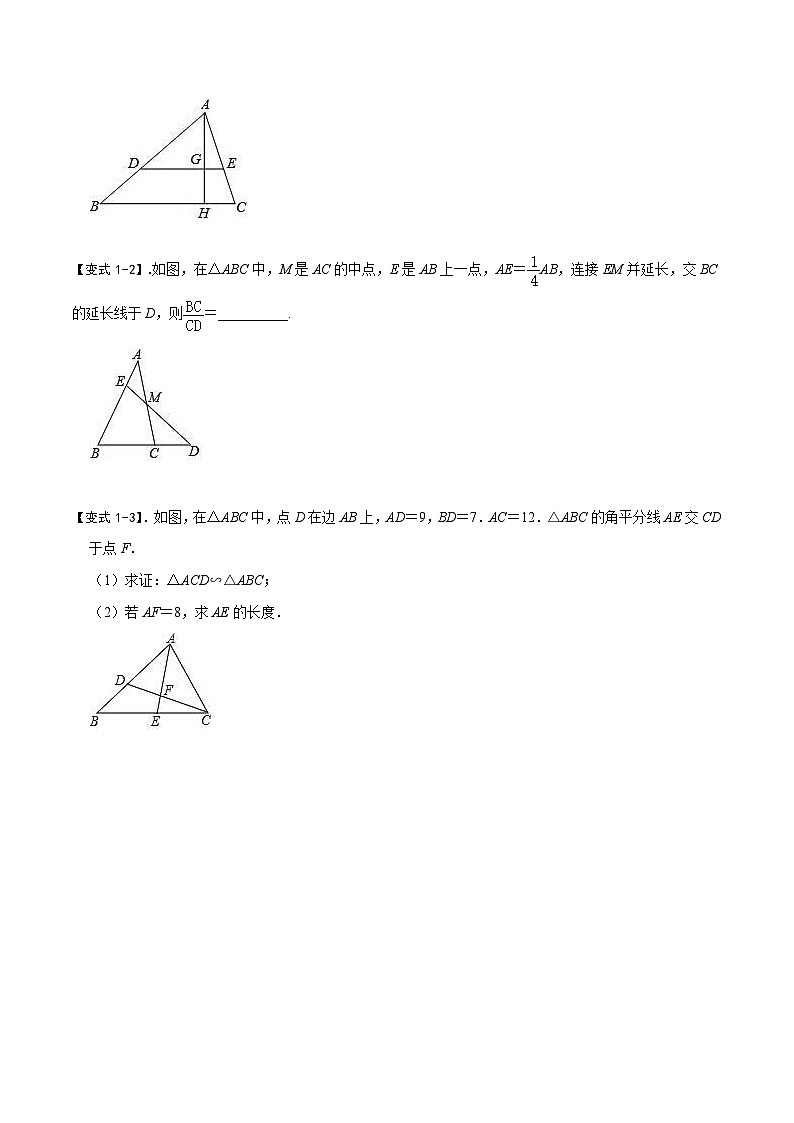
【变式1-2】.如图,在△ABC中,M是AC的中点,E是AB上一点,AE=AB,连接EM并延长,交BC的延长线于D,则=__________.
解:如图,过C点作CP∥AB,交DE于P,
∵PC∥AE, ∴△AEM∽△CPM, ∴=,
∵M是AC的中点, ∴AM=CM, ∴PC=AE,
∵AE=AB, ∴CP=AB, ∴CP=BE,
∵CP∥BE, ∴△DCP∽△DBE,
∴==, ∴BD=3CD,
∴BC=2CD,即=2.
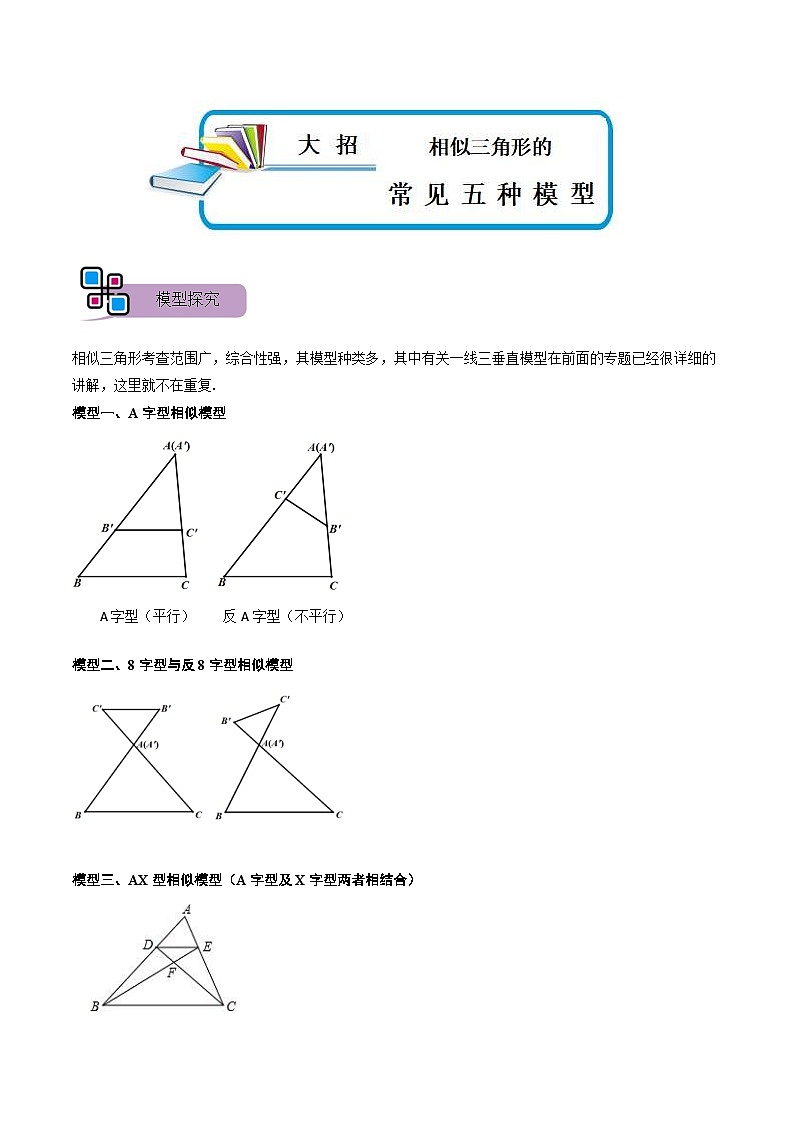
【变式1-3】.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)若AF=8,求AE的长度.
解:(1)∵AD=9,BD=7,AC=12,
∴AB=AD+BD=16,
∵==,==,
∴=,
∵∠BAC=∠CAD,
∴△ACD∽△ABC;
(2)由(1)可知,△ACD∽△ABC,
∴∠ABE=∠ACF,
∵AE平分∠BAC,
∴∠BAE=∠CAF,
∴△ABE∽△ACF,
∴=,即=,
∴AE==.
考点二、8字与反8字相似模型
【例2】.如图,AG∥BD,AF:FB=1:2,BC:CD=2:1,求的值
解:∵AG∥BD,
∴△AFG∽△BFD, ∴=,
∵,∴CD=BD, ∴,
∵AG∥BD,
∴△AEG∽△CED, ∴.
变式训练
【变式2-1】.如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )
A.B.C.D.
解:A、∵AB∥CD,
∴=,故本选项不符合题目要求;
B、∵AE∥DF,
∴△CEG∞△CDH,
∴=,∴=,
∵AB∥CD,
∴=,∴=,
∴=,∴=,故本选项不符合题目要求;
∵AB∥CD,AE∥DF,
∴四边形AEDF是平行四边形,∴AF=DE,
∵AE∥DF,
∴,∴=,故本选项不符合题目要求;
D、∵AE∥DF,
∴△BFH∞△BAG,∴,故本选项符合题目要求;故选:D.
【变式2-2】.如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为( )
A.8B.10C.12D.14
解:如图,∵四边形ABCD是平行四边形,
∵EA∥BC,
∴△AEF∽△CBF,
∵AE=DE=AD,CB=AD,
∴====,
∴AF=AC,EF=BF,
∴S△ABF=S△ABC,
∴S△AEF=S△ABF=×S△ABC=S△ABC,
∵S△AEF=2,
∴S△ABC=6S△AEF=6×2=12,故选:C.
【变式2-3】.如图,锐角三角形ABC中,∠A=60°,BE⊥AC于E,CD⊥AB于D,则DE:BC= 1:2 .
解:如图,∵在△ADC中,∠A=60°,CD⊥AB于点D,
∴∠ACD=30°,
∴=.
又∵在△ABE中,∠A=60°,BE⊥AC于E,
∴∠ABE=30°,
∴=,
∴=.
又∵∠A=∠A,
∴△ADE∽△ACB,
∴DE:BC=AD:AC=1:2.故答案是:1:2.
考点三、AX型相似模型(A字型及X字型两者相结合)
【例3】.如图,在△ABC中,点D和E分别是边AB和AC的中点,连接DE,DC与BE交于点O,若△DOE的面积为1,则△ABC的面积为( )
A.6B.9C.12D.13.5
解:∵点D和E分别是边AB和AC的中点,
∴O点为△ABC的重心,
∴OB=2OE,
∴S△BOD=2S△DOE=2×1=2,
∴S△BDE=3,
∵AD=BD,
∴S△ABE=2S△BDE=6,
∵AE=CE,
∴S△ABC=2S△ABE=2×6=12.故选C.
变式训练
【变式3-1】.如图,DE是△ABC的中位线,F为DE中点,连接AF并延长交BC于点G,若S△EFG=1,则S△ABC= 24 .
解:方法一:∵DE是△ABC的中位线,
∴D、E分别为AB、BC的中点,
如图过D作DM∥BC交AG于点M,
∵DM∥BC,
∴∠DMF=∠EGF,
∵点F为DE的中点,
∴DF=EF,
在△DMF和△EGF中,
,
∴△DMF≌△EGF(AAS),
∴S△DMF=S△EGF=1,GF=FM,DM=GE,
∵点D为AB的中点,且DM∥BC,
∴AM=MG,
∴FM=AM,
∴S△ADM=2S△DMF=2,
∵DM为△ABG的中位线,
∴=,
∴S△ABG=4S△ADM=4×2=8,
∴S梯形DMGB=S△ABG﹣S△ADM=8﹣2=6,
∴S△BDE=S梯形DMGB=6,
∵DE是△ABC的中位线,
∴S△ABC=4S△BDE=4×6=24,
方法二:连接AE,
∵DE是△ABC的中位线,
∴DE∥AC,DE=AC,
∵F是DE的中点,
∴=,
∴==,
∵S△EFG=1,
∴S△ACG=16,
∵EF∥AC,
∴==,
∴==,
∴S△AEG=S△ACG=4,
∴S△ACE=S△ACG﹣S△AEG=12,
∴S△ABC=2S△ACE=24,故答案为:24.
【变式3-2】.如图:AD∥EG∥BC,EG交DB于点F,已知AD=6,BC=8,AE=6,EF=2.
(1)求EB的长; (2)求FG的长.
解:(1)∵EG∥AD,
∴△BAD∽△BEF,
∴=,即=,
∴EB=3.
(2)∵EG∥∥BC,
∴△AEG∽△ABC,
∴=,即=,
∴EG=,
∴FG=EG﹣EF=.
【变式3-3】.如图,已知AB∥CD,AC与BD相交于点E,点F在线段BC上,,.
(1)求证:AB∥EF;
(2)求S△ABE:S△EBC:S△ECD.
(1)证明:∵AB∥CD,
∴==,
∵,
∴=,
∴EF∥CD,
∴AB∥EF.
(2)解:设△ABE的面积为m.
∵AB∥CD,
∴△ABE∽△CDE,
∴=()2=,
∴S△CDE=4m,
∵==,
∴S△BEC=2m,
∴S△ABE:S△EBC:S△ECD=m:2m:4m=1:2:4.
模型四、子母型相似模型
【例4】.如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证:
(1)△ACP∽△PDB,
(2)CD2=AC•BD.
证明:(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=∠CPD=60°,
∴∠ACP=∠PDB=120°,
∵∠APB=120°,
∴∠APC+∠BPD=60°,
∵∠CAP+∠APC=60°
∴∠BPD=∠CAP, ∴△ACP∽△PDB;
(2)由(1)得△ACP∽△PDB,
∴,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴,
∴CD2=AC•BD.
变式训练
【变式4-1】.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠CB.∠APB=∠ABCC.D.
解:在△ABP和△ACB中,∠BAP=∠CAB,
∴当∠ABP=∠C时,满足两组角对应相等,可判断△ABP∽△ACB,故A正确;
当∠APB=∠ABC时,满足两组角对应相等,可判断△ABP∽△ACB,故B正确;
当时,满足两边对应成比例且夹角相等,可判断△ABP∽△ACB,故C正确;
当时,其夹角不相等,则不能判断△ABP∽△ACB,故D不正确;
故选:D.
【变式4-2】.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC+∠BDC=180°,AD=2,CD=4,则AB的长为( )
A.3B.4C.D.2
解:∵∠ABC+∠BDC=180°,∠ADB+∠BDC=180°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABC∽△ADB,
∴,
∵AD=2,CD=4,
∴,
∴AB2=12,
∴AB=2或﹣2(不合题意,舍去),故选:D.
【变式4-3】.如图,边长为4的正方形,内切圆记为圆O,P为圆O上一动点,则PA+PB的最小值为 2 .
解:设⊙O半径为r,
OP=r=BC=2,OB=r=2,
取OB的中点I,连接PI,
∴OI=IB=,
∵,
,
∴,
∠O是公共角,
∴△BOP∽△POI,
∴,
∴PI=PB,
∴AP+PB=AP+PI,
∴当A、P、I在一条直线上时,AP+PB最小,
作IE⊥AB于E,
∵∠ABO=45°,
∴IE=BE=BI=1,
∴AE=AB﹣BE=3,
∴AI==,
∴AP+PB最小值=AI=,
∵PA+PB=(PA+PB),
∴PA+PB的最小值是AI==2.
故答案是2.
模型五、手拉手相似模型
【例5】.如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为 .
解:连接OA、OD,
∵△ABC与△DEF均为等边三角形,O为BC、EF的中点,
∴AO⊥BC,DO⊥EF,∠EDO=30°,∠BAO=30°,
∴OD:OE=OA:OB=:1,
∵∠DOE+∠EOA=∠BOA+∠EOA 即∠DOA=∠EOB,
∴△DOA∽△EOB,
∴OD:OE=OA:OB=AD:BE=:1=,故答案为:.
变式训练
【变式5-1】.如图,在△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
求证:(1)△BAC∽△DAE; (2)△BAD∽△CAE.
证明:(1)∵∠BAC=∠DAE,∠ABC=∠ADE.
∴△BAC∽△DAE;
(2)∵△BAC∽△DAE,
∴,
∴,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△BAD∽△CAE.
【变式5-2】.如图,点D是△ABC内一点,且∠BDC=90°,AB=2,AC=,∠BAD=∠CBD=30°,AD= .
解:如图,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,
∵∠BAD=30°,
∴∠DAM=60°,
∴∠AMD=30°,
∴∠AMD=∠DBC,
又∵∠ADM=∠BDC=90°,
∴△BDC∽△MDA,
∴,
又∠BDC=∠MDA,
∴∠BDC+∠CDM=∠ADM+∠CDM,
即∠BDM=∠CDA,
∴△BDM∽△CDA,
∴=,
∵AC=,
∴BM=3,
在Rt△ABM中,AM===,∴AD=AM=.
【变式5-3】.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),则BD的长为 .(用含k的式子表示)
解:如图中,∵AE⊥BC,BE=EC,
∴AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=4k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG==.
∴BD=CG=,
故答案为:.
实战演练
1.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
A.=B.C.D.
解:A、∵EF∥AB,
∴=,
∵DE∥BC,
∴=,
∴=,故A正确,
B、易知△ADE∽△EFC,
∴=,
∴=,故B正确.
C、∵△CEF∽△CAB,
∴=,
∴=,故C正确.
D、∵DE∥BC,
∴=,
显然DE≠CF,故D错误.故选:D.
2.如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
A.2:3B.2:5C.4:9D.:
解:∵AD∥BC,
∴∠ACB=∠DAC
又∵∠B=∠ACD=90°,
∴△CBA∽△ACD
===,
∵=()2=
∴△ABC与△DCA的面积比为4:9.故选:C.
3.如图,菱形ABCD中,E点在BC上,F点在CD上,G点、H点在AD上,且AE∥HC∥GF.若AH=8,HG=5,GD=4,则下列选项中的线段,何者长度最长?( )
A.CFB.FDC.BED.EC
解:∵AH=8,HG=5,GD=4,
∴AD=8+5+4=17,
∵四边形ABCD为菱形,
∴BC=CD=AD=17,
∵AE∥HC,AD∥BC,
∴四边形AECH为平行四边形,
∴CE=AH=8,
∴BE=BC﹣CE=17﹣8=9,
∵HC∥GF,
∴=,即=,
解得:DF=,
∴FC=17﹣=,
∵>9>8>,
∴CF长度最长,故选:A.
4.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为( )
A.6B.9C.12D.18
解:如图,延长BQ交射线EF于M,
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
∵CQ=CE,
∴EQ=2CQ,
由EF∥BC得,△MEQ∽△BCQ,
∴=2,
∴EM=2BC=2×6=12,
即EP+BP=12.故选:C.
5.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2,AD=2,将△ABC绕点C顺时针方向旋转后得△A′B′C,当A′B′恰好经过点D时,△B′CD为等腰三角形,若BB′=2,则AA′等于( )
A.B.2C.D.
解:过D作DE⊥BC于E,
则BE=AD=2,DE=2,
设B′C=BC=x,
则DC=x,
∴DC2=DE2+EC2,即2x2=28+(x﹣2)2,
解得:x=4(负值舍去),
∴BC=4,AC=,
∵将△ABC绕点C顺时针方向旋转后得△A′B′C,
∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,
∴
∴△A′CA∽△B′CB,
∴,即
∴AA′=,故选:A.
6.如图,已知,△ABC中边AB上一点P,且∠ACP=∠B,AC=4,AP=2,则BP= 6 .
解:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
∴AC2=AP•AB,即AB=AC2÷AP=16÷2=8,
∴BP=AB﹣AP=6.
7.如图,在▱ABCD中,AC、BD相交于点O,点E是OA的中点,联结BE并延长交AD于点F,如果△AEF的面积是4,那么△BCE的面积是 36 .
解:∵在▱ABCD中,AO=AC,
∵点E是OA的中点,
∴AE=CE,
∵AD∥BC,
∴△AFE∽△CBE,
∴==,
∵S△AEF=4,=( )2=,
∴S△BCE=36,故答案为36.
8.如图,在△ABC中,点G为ABC的重心,过点G作DE∥AC分别交边AB、BC于点D、E,过点D作DF∥BC交AC于点F,如果DF=4,那么BE的长为 8 .
解:连接BG并延长交AC于H,
∵G为ABC的重心,
∴=2,
∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,
∴CE=DF=4,
∵GE∥CH,
∴△BEG∽△CBH,
∴=2,
∴BE=8,故答案为:8.
9.如图,已知Rt△ABC中,两条直角边AB=3,BC=4,将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,并且点A落在DE边上,则sin∠ABE= .
解:∵将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,
∴BD=AB,BC=BE,∠ABD=∠CBE,∠DEB=∠ACB,
∴∠D=∠BAC=∠BAD=(180°﹣∠ABD),
∴∠BEC=(180°﹣∠CBE),
∴∠D=∠BEC,
∵∠ABC=∠DBE=90°,
∴∠DEB+∠BEC=90°,
∴∠AEC=90°,
∵∠AGB=∠EGC,
∴∠ACE=∠ABE,
∵在Rt△ABC中,AB=3,BC=4,
∴AC=DE=5,
过B作BH⊥DE于H,
则DH=AH,BD2=DH•DE,
∴DH==,
∴AD=,
∴AE=DE﹣AD=,
∴sin∠ABE=sin∠ACE===, 故答案为:.
10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
解:(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,
∴CD=2,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,
∴BC=6,
∴BD=BC﹣CD=4,
∵DE∥CA,
∴,
∴DE=4;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,
∴,
∵BD=4,BC=6,DF=AG,
∴.
11.如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC于点M,且∠ADE=∠CDF.
(1)求证:CE=AF;
(2)连接ME,若=,AF=2,求ME的长.
解:(1)∵四边形ABCD是菱形,
∴AD=CD,∠DAF=∠DCE,
又∵∠ADE=∠CDF,
∴∠ADE﹣∠EDF=∠CDF﹣∠EDF,
∴∠ADF=∠CDE,
在△ADF和△CDE中,
,
∴△ADF≌△CDE,
∴CE=AF.
(2)∵四边形ABCD是菱形,
∴AB=BC,
由(1)得:CE=AF=2,
∴BE=BF,
设BE=BF=x,
∵=,AF=2,
∴,解得x=,
∴BE=BF=,
∵=,且CE=AF,
∴==,
∵∠CMD=∠AMF,∠DCM=∠AMF,
∴△AMF∽△CMD,
∴,
∴=,且∠ACB=∠ACB
∴△ABC∽△MEC
∴∠CAB=∠CME=∠ACB
∴ME=CE=2
12.[问题背景](1)如图①,已知△ABC∽△ADE,求证:△ABD∽△ACE.
[尝试应用](2)如图②,在△ABC和△ADE中,∠BAC=∠DAE=90°
∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,
①填空:= 1 ;
②求的值.
(1)证明:如图①,∵△ABC∽△ADE,
∴∠BAC=∠DAE,=,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,=,
∴∠BAD=∠CAE,
∴△ABD∽△ACE.
(2)解:①如图②,∵∠DAE=90°,∠ADE=30°,
∴DE=2AE,
∴AD===AE,
∵=,
∴AD=BD,
∴AE=BD,
∴=1,
故答案为:1.
②如图②,连接CE,
∵∠BAC=∠DAE=90°,∠ABC=∠ADE,
∴△BAC∽△CAE,
∴=,
∴=,
∵∠BAD=∠CAE=90°﹣∠CAD,
∴△BAD∽△CAE,
∴∠ABC=∠ACE,
∴∠ADE=∠ACE,
∵∠AFD=∠EFC,
∴△AFD∽△EFC,
∴=,
由①得AD=AE,AD=BD,
∴==,
∴BD=CE,
∴AD=×CE=3CE,
∴=3,
∴=3,
∴的值是3.
13.如图,在正方形ABCD中,AB=4,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于点M、N,连接EN、EF.
(1)求证:△ABN∽△MBE;
(2)求证:BM2+ND2=MN2;
(3)①求△CEF的周长;
②若点G、F分别是EF、CD的中点,连接NG,则NG的长为 .
(1)证明:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=90°,
∴∠ABD=∠ADB=45°,
∴∠ABN=∠MBE=45°,∠BME=∠ABD+∠BAM=45°+∠BAM,
∵∠EAF=45°,
∴∠BAN=∠EAF+∠BAM=45°+∠BAM,
∴∠BAN=∠BME,
∴△ABN∽△MBE.
(2)证明:如图1,将△ADN绕点A顺时针旋转90°得到△ABH,连接MH,
∴∠BAH=∠DAN,AH=AN,HB=ND,
∵∠MAN=∠EAF=45°,
∴∠MAH=∠BAH+∠BAM=∠DAN+∠BAM=45°,
∴∠MAH=∠MAN,
∵AM=AM,
∴△MAH≌△MAN(SAS),
∴MH=MN,
∵∠ABH=∠ADN=45°,
∴∠MBH=∠ABD+∠ABH=90°,
∴BM2+HB2=MH2,
∴BM2+ND2=MN2.
(3)解:①如图2,将△ADF绕点A顺时针旋转90°得到△ABK,
∴AK=AF,∠BAK=∠DAF,BK=DF,∠ABK=∠ADF=90°,
∴∠ABK+∠ABE=180°,
∴点K、点B、点E在同一条直线上,
∵∠EAK=∠BAE+∠BAK=∠BAE+∠DAF=45°,
∴∠EAK=∠EAFM,
∵AE=AE,
∴△EAK≌△EAF(SAS),
∴EK=EF,
∴BE+DF=BE+BK=EK=EF,
∵CB=CD=AB=4,
∴CE+EF+CF=CE+BE+DF+CF=CB+CD=4+4=8,
∴△CEF的周长是8.
②如图2,∵F是CD的中点,
∴CF=DF=CD=2,
∵∠C=90°,
∴CF2+EF2=CE2,
∵EF=BE+DF=BE+2,CE=CB﹣BE=4﹣BE,
∴22+(4﹣BE)2=(BE+2)2,
解得BE=,
∴EF=+2=,
∵∠MBE=∠MAN=45°,∠BME=∠AMN,
∴△BME∽△AMN,
∴=,
∴=,
∴∠AMB=∠NME,
∴△AMB∽△NME,
∴∠NEM=∠ABM=45°,
∴∠ENF=∠MAN+∠NEM=90°,
∵G是EF的中点,
∴NG=EF=×=,
故答案为:.
14.问题背景 如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;
尝试应用 如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,求的值;
拓展创新 如图(3),D是△ABC内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB=4,AC=2,直接写出AD的长.
问题背景
证明:∵△ABC∽△ADE,
∴,∠BAC=∠DAE,
∴∠BAD=∠CAE,,
∴△ABD∽△ACE;
尝试应用
解:如图1,连接EC,
∵∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,
∴△ABC∽△ADE,
由(1)知△ABD∽△ACE,
∴,∠ACE=∠ABD=∠ADE,
在Rt△ADE中,∠ADE=30°,
∴,
∴=3.
∵∠ADF=∠ECF,∠AFD=∠EFC,
∴△ADF∽△ECF,
∴=3.
拓展创新
解:如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,
∵∠BAD=30°,
∴∠DAM=60°,
∴∠AMD=30°,
∴∠AMD=∠DBC,
又∵∠ADM=∠BDC=90°,
∴△BDC∽△MDA,
∴,
又∠BDC=∠MDA,
∴∠BDC+∠CDM=∠ADM+∠CDM,
即∠BDM=∠CDA,
∴△BDM∽△CDA,
∴,
∵AC=2,
∴BM=2=6,
∴在Rt△ABM中,AM===2,
∴AD=.
15.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的数量关系 BG=DE 及所在直线的位置关系 BG⊥DE ;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;
(2)将原题中正方形改为矩形(如图4﹣6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k>0),则线段BG、线段DE的数量关系 = 及所在直线的位置关系 BG⊥DE ;
(3)在第(2)题图5中,连接DG、BE,且a=4,b=3,k=,直接写出BE2+DG2的值为 .
解:(1)①猜想:BG⊥DE,BG=DE;
故答案为:BG=DE,BG⊥DE;
②结论成立.
理由:如图2中,∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠CBG+∠BHC=90°,
∴∠CDE+∠DHG=90°,
∴BG⊥DE.
(2)∵AB=a,BC=b,CE=ka,CG=kb,
∴==,
又∵∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,==,
又∵∠CBG+∠BHC=90°,
∴∠CDE+∠DHG=90°,
∴BG⊥DE.
故答案为:=,BG⊥DE.
(3)连接BE、DG.
根据题意,得AB=4,BC=3,CE=2,CG=1.5,
∵BG⊥DE,∠BCD=∠ECG=90°
∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+16+2.25+4=.
相关试卷
这是一份中考数学二轮复习满分突破几何模型练习专题12 半角模型(2份打包,原卷版+解析版),文件包含中考数学二轮复习满分突破几何模型练习专题12半角模型原卷版doc、中考数学二轮复习满分突破几何模型练习专题12半角模型解析版doc等2份试卷配套教学资源,其中试卷共86页, 欢迎下载使用。
这是一份模型05 相似三角形中的常见五种基本模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型05相似三角形中的常见五种基本模型原卷版docx、模型05相似三角形中的常见五种基本模型解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
这是一份中考数学二轮培优复习《几何模型》专题08 相似三角形中的基本模型(2份打包,原卷版+教师版),文件包含中考数学二轮培优复习《几何模型》专题08相似三角形中的基本模型教师版doc、中考数学二轮培优复习《几何模型》专题08相似三角形中的基本模型学生版doc等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。









