适用于新高考新教材备战2025届高考数学一轮总复习第11章计数原理概率随机变量及其分布解答题专项6概率与统计中的综合问题课件新人教A版

这是一份适用于新高考新教材备战2025届高考数学一轮总复习第11章计数原理概率随机变量及其分布解答题专项6概率与统计中的综合问题课件新人教A版，共43页。PPT课件主要包含了所以X的分布列为，故列联表为等内容，欢迎下载使用。

考情分析:有关概率、统计与其他知识相交汇的考题,能体现“返璞归真,支持课改;突破定势,考查真功”的命题理念,是每年高考的常考内容.近几年还经常将概率与统计问题与数列、函数、导数结合,成为创新问题.
考点一 统计图表与分布列的综合问题
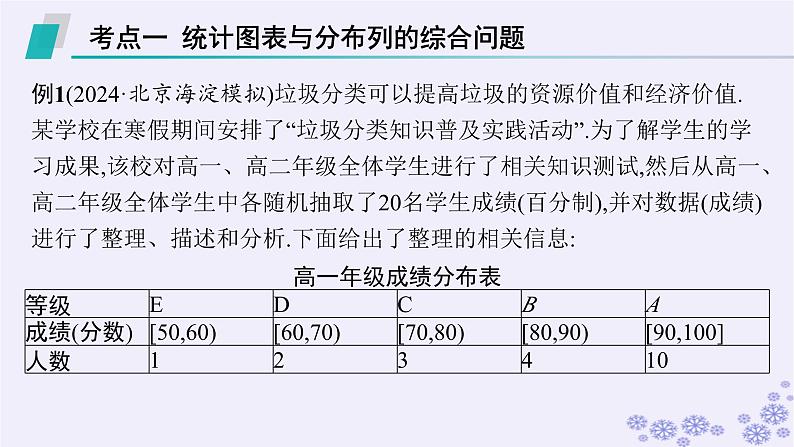
例1(2024·北京海淀模拟)垃圾分类可以提高垃圾的资源价值和经济价值.某学校在寒假期间安排了“垃圾分类知识普及实践活动”.为了解学生的学习成果,该校对高一、高二年级全体学生进行了相关知识测试,然后从高一、高二年级全体学生中各随机抽取了20名学生成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了整理的相关信息:高一年级成绩分布表
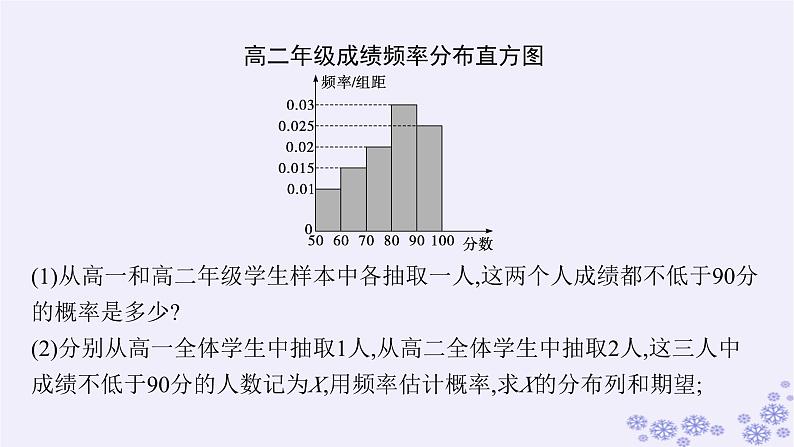
高二年级成绩频率分布直方图
(1)从高一和高二年级学生样本中各抽取一人,这两个人成绩都不低于90分的概率是多少?(2)分别从高一全体学生中抽取1人,从高二全体学生中抽取2人,这三人中成绩不低于90分的人数记为X,用频率估计概率,求X的分布列和期望;
(3)学校为提高学生对垃圾分类的了解情况需要在高一或高二进行一场讲座,假设讲座能够使学生成绩普遍提高一个等级,若高一、高二学生数量一致,那么若想高一和高二学生的平均分尽可能高,需要在高一讲座还是高二讲座?(直接写出结论)
(3)由于高一年级低分段的人数相比高二年级要少得多,所以需要在高二讲座.
考点二 回归模型与分布列的综合问题
例2(2024·浙江绍兴模拟)今年春季以来,各地出台了促进经济发展的各种措施,经济增长呈现稳中有进的可喜现象.服务业的消费越来越火爆,一些超市也纷纷加大了广告促销.现在某地随机抽取了7家超市,得到其广告支出x(单位:万元)与销售额y(单位:万元)数据如下:
(1)建立y关于x的一元线性回归方程(系数精确到0.01);(2)若将超市的销售额y与广告支出x的比值称为该超市的广告效率值μ,当μ≥10时,称该超市的广告为“好广告”.从这7家超市中随机抽取4家超市,记这4家超市中“好广告”的超市数为X,求X的分布列与数学期望.
[对点训练1](2024·四川成都模拟)为研究如何合理施用化肥,使其最大限度地促进粮食增产,减少对周围环境的污染,某研究团队收集了10组化肥施用量和粮食亩产量的数据,并对这些数据进行了初步处理,得到如图所示的散点图及如表所示的一些统计量的值,其中,化肥施用量为x(单位:千克),粮食亩产量为y(单位:百千克).令ti=ln xi,zi=ln yi(i=1,2,…,10).
(1)根据散点图,判断y=a+bx与y=cxd哪一个更适宜作为粮食亩产量y关于化肥施用量x的回归方程模型(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程,并估计化肥施用量为27千克时,粮食亩产量的值;
(3)经生产技术提高后,该化肥的有效率Z大幅提高,经试验统计得Z大致服从正态分布N(0.54,0.022).问这种化肥的有效率超过56%的概率约为多少?
②若随机变量Z~N(μ,σ2),则有P(μ-σ≤Z≤μ+σ)≈0.682 7,P(μ-2σ≤Z≤μ+2σ)≈0.954 5;③e≈2.7.
解 (1)由散点图可知y随x的变化呈非线性的变化趋势,∴y=cxd更适宜作为y关于x的回归方程模型.
(3)∵Z~N(0.54,0.022),则μ=0.54,σ=0.02,∴P(μ-σ≤Z≤μ+σ)=P(0.52≤Z≤0.56)≈0.682 7,则P(Z>0.56) =0.158 65,∴这种化肥的有效率超过56%的概率约为0.158 65.
考点三 独立性检验与分布列的综合问题
例3(12分)(2023·全国甲,理19)一项试验旨在研究臭氧效应,试验方案如下:选40只小白鼠,随机地将其中20只分配到试验组,另外20只分配到对照组,试验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).(1)设X表示指定的两只小白鼠中分配到对照组的只数,求X的分布列和数学期望;关键点:结合题意弄清楚X服从的是超几何分布还是二项分布.
(2)试验结果如下:对照组的小白鼠体重的增加量从小到大排序为15.2　18.8　20.2　21.3　22.5　23.2　25.8　26.5　27.5　30.1　32.6　34.3　34.8　35.6　35.6　35.8　36.2　37.3　40.5　43.2试验组的小白鼠体重的增加量从小到大排序为7.8　9.2　11.4　12.4　13.2　15.5　16.518.0　18.8　19.2　19.8　20.2　21.6　22.823.6　23.9　25.1　28.2　32.3　36.5
(ⅰ)求40只小白鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于m的数据的个数,完成如下列联表:
突破口:易知中位数是从小到大排序后第20位与第21位数据的平均数.通过整理可得第20位数据为23.2,第21位数据为23.6.(ⅱ)根据(ⅰ)中的列联表,能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
审题指导:(1)利用超几何分布的知识即可求得分布列及数学期望;(2)(i)根据中位数的定义即可求得m=23.4,从而求得列联表;(ii)利用独立性检验的卡方计算进行检验,对照附表结合题意作答.
规范解答:解 (1)由题意,X服从超几何分布,X的可能取值为0,1,2,则
X服从超几何分布,且N=40,M=20,n=2
①注意大小排序;②偶数个数的中位数是中间两个数的平均数
(ii)零假设为H0:小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量无差异.
因为判断是否有95%的把握,所以临界值取3.841,而不是6.635
[对点训练2](12分)(2024·浙江宁波模拟)盲盒,是指消费者不能提前得知具体产品款式的玩具盒子,具有随机属性.某品牌推出2款盲盒套餐,A款盲盒套餐包含4款不同单品,且必包含隐藏款X;B款盲盒套餐包含2款不同单品,有50%的可能性出现隐藏款X.为避免盲目购买与黄牛囤积,每人每天只能购买1件盲盒套餐.开售第二日,销售门店对80名购买了套餐的消费者进行了问卷调查,得到如下列联表:
(1)根据2×2列联表,判断是否有99%的把握认为A,B款盲盒套餐的选择与年龄有关;(2)甲、乙、丙三人每人购买1件B款盲盒套餐,记随机变量ξ为其中隐藏款X的个数,求ξ的分布列和数学期望;(3)某消费者在开售首日与次日分别购买了A款盲盒套餐与B款盲盒套餐各1件,并将6件单品全部打乱放在一起,从中随机抽取1件打开后发现为隐藏款X,求该隐藏款来自B款盲盒套餐的概率.
解 (1)零假设为H0:A,B款盲盒套餐的选择与年龄之间无关联.
(3)设A表示事件“随机抽取1件打开后发现为隐藏款X”,设B1表示事件“随机抽取的1件单品来自A款盲盒套餐”,设B2表示事件“随机抽取的1件单品来自B款盲盒套餐”,
考点四 概率统计与函数、导数的综合问题
例4(2023·新高考Ⅱ,19)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);误诊率是将未患病者判定为阳性的概率,记为q(c).假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.(1)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c);(2)设函数f(c)=p(c)+q(c).当c∈[95,105]时,求f(c)的解析式,并求f(c)在区间[95,105]的最小值.
解 (1)当p(c)=0.5%时,由患病者频率分布直方图可得第一个小矩形面积为0.002×5=0.01,
由未患病者频率分布直方图可得q(c)=0.01×(100-97.5)+0.002×5=0.035.
(2)当c∈[95,100)时,p(c)=(c-95)×0.002,q(c)=(100-c)×0.01+0.01,∴f(c)=-0.008c+0.82>0.02;当c∈[100,105]时,p(c)=5×0.002+(c-100)×0.012,q(c)=(105-c)×0.002,∴f(c)=0.01c-0.98≥0.02.
故当c=100时,f(c)取最小值,最小值为f(100)=0.02.
[对点训练3](2021·新高考Ⅱ,21)一种微生物群体可以经过自身繁殖不断生存下去,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代,……,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3).(1)已知p0=0.4,p1=0.3,p2=0.2,p3=0.1,求E(X).(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程:p0+p1x+p2x2+p3x3=x的一个最小正实根,求证:当E(X)≤1时,p=1;当E(X)>1时,p<1.(3)根据你的理解说明(2)问结论的实际意义.
(1)解 E(X)=0×0.4+1×0.3+2×0.2+3×0.1=1.
(2)证明 (方法一)令f(x)=p0+p1x+p2x2+p3x3-x,有f'(x)=p1+2p2x+3p3x2-1, f″(x)=2p2+6p3x.显然当x≥0时,f″(x)=2p2+6p3x>0,f'(x)在区间[0,+∞)上单调递增,下面证明当E(X)≤1时,有p=1.假设p<1.一方面,因为f(p)=0,f(1)=0,根据罗尔中值定理,∃ξ∈(p,1),使得f'(ξ)=0.另一方面,因为f'(x)在区间[0,+∞)上单调递增,所以有f'(ξ)1时,p<1.
因为f'(1)=E(X)-1>0,考虑到f'(x)是一个连续函数,所以存在x=1的某一邻域U(1),使得当x∈U(1)时,有f'(x)>0.在这个邻域内任取一点x0<1,有f(x0)0,且f(x)是一个连续函数,所以由零点存在定理,至少存在一点η∈(0,x0),使得f(η)=0.因为p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根,于是p≤η<1.
(方法二)令f(x)=p0+p1x+p2x2+p3x3-x,当x>0时,有f'(x)=p1+2p2x+3p3x2-1, f″(x)=2p2+6p3x>0.当x≥0时,f″(x)=2p2+6p3x>0,所以f'(x)在区间[0,+∞)上单调递增,下面证明当E(X)≤1时,有p=1.当x∈(0,1)时,因为f'(x)f(1)=0,即f(x)在(0,1)内没有零点,所以x=1是使得f(x)=0的最小的正根.故p=1.当E(X)>1时,因为f'(0)=p1-1<0, f'(1)=E(X)-1>0且f'(x)在[0,1]上连续,所以由零点存在定理知,存在x0∈(0,1),使得f'(x0)=0.因为f'(x)在区间[0,+∞)上单调递增,所以当x0f'(x0)=0,所以函数f(x)在[x0,1]上单调递增,于是f(x0)0,由零点存在定理知,存在t∈(0,x0),使得f(t)=0.另一方面,由于当0(方法三)设f(x)=p3x3+p2x2+p1x+p0-x,则有f(1)=p3+p2+p1+p0-1=0.f'(x)=3p3x2+2p2x+p1-1,则有f'(1)=3p3+2p2+p1-1=E(X)-1.
并且因为3p3>0,所以当xx2时,f'(x)>0,所以函数f(x)在区间(-∞,x1)和区间(x2,+∞)上单调递增;当x1f(1)=0,即方程f(x)=0在(0,1)内没有根,所以p=1就是f(x)=0的最小正根.
当E(X)>1时,f'(1)=E(X)-1>0,此时,必有x2<1.因为函数f(x)在[x2,+∞)上单调递增,所以f(x2)0以及函数f(x)的连续性,由零点存在定理知在0与1之间必有函数f(x)的零点,此零点就是原方程的一个正根,且比1小,故p<1.
(方法四)由题意知p0+p1+p2+p3=1,E(X)=p1+2p2+3p3.方程p0+p1x+p2x2+p3x3=x变形为p0-(1-p1)x+p2x2+p3x3=0,考虑到1-p1=p0+p2+p3,于是原方程又可以写成p0-(p0+p2+p3)x+p2x2+p3x3=0,即p0(1-x)+p2x(x-1)+p3x(x+1)(x-1)=0,即(x-1)[p3x2+(p2+p3)x-p0]=0.令g(x)=p3x2+(p2+p3)x-p0,因为Δ=(p2+p3)2+4p0p3>0,所以g(x)有两个不相等
这样原方程最多只有两个正根x=1和x=x2.显然,当xx2时,有g(x)>0,当x11时,g(1)=E(X)-1>0,这说明1>x2,此时原方程的最小正根为x2.
(方法五)由题意知p0+p1+p2+p3=1,E(X)=p1+2p2+3p3.方程p0+p1x+p2x2+p3x3=x变形为p0-(1-p1)x+p2x2+p3x3=0,考虑到1-p1=p0+p2+p3,于是原方程又可以写成p0-(p0+p2+p3)x+p2x2+p3x3=0,即p0(1-x)+p2x(x-1)+p3x(x+1)(x-1)=0,即(x-1)[p3x2+(p2+p3)x-p0]=0.
因为g(0)=-p0<0,g(1)=2p3+p2-p0=p1+2p2+3p3-1=E(X)-1,p3>0,所以当E(X)≤1时,g(1)≤0,g(x)的正实根x0≥1,原方程的最小正实根p=1,当E(X)>1时,g(1)>0,g(x)的正实根x0<1,原方程的最小正实根p=x0<1.