




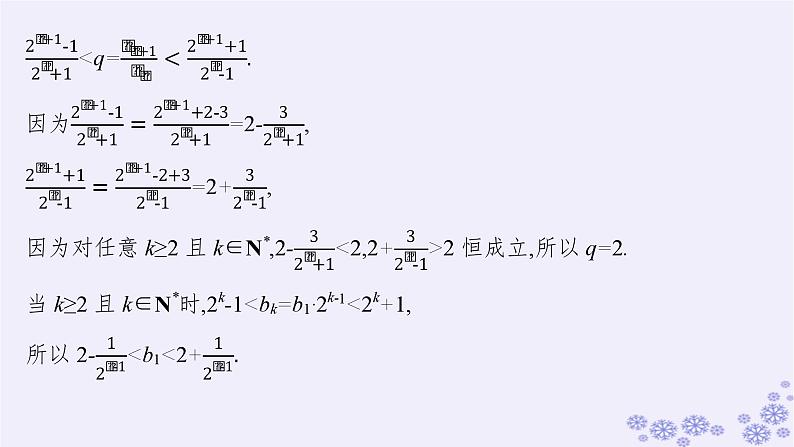


适用于新高考新教材备战2025届高考数学一轮总复习第6章数列解答题专项3数列中的综合问题课件新人教A版
展开考情分析:数列是高考考查的重要内容,也是高考解答题的必考点.从近几年的高考试题来看,数列解答题的命题趋势是稳中求变、变中求新、新中求活,以考查数列的基本知识、基本方法为主,渗透综合应用能力的考查.题目涉及的主要知识点、难度、新颖度有很大的变化空间.对数学抽象、数学运算、逻辑推理等数学核心素养都有较深入的考查.
考点一 等差数列、等比数列的综合问题
例1(2023·天津,19)已知{an}是等差数列,a2+a5=16,a5-a3=4.
(2)已知{bn}为等比数列,对于任意k∈N*,若2k-1≤n≤2k-1,则bk
(2)①对于任意k∈N*,若2k-1≤n≤2k-1,则2k+1≤2n+1≤2k+1-1,又因为bk
(1)证明 设等差数列的公差为d,由a2-b2=a3-b3,得a1+d-2b1=a1+2d-4b1,得d=2b1.由a2-b2=b4-a4,可得a1+d-2b1=8b1-(a1+3d),可得a1+2b1-2b1=8b1-(a1+6b1),整理可得a1=b1,得证.
(2)解 由(1)知d=2b1=2a1,由bk=am+a1,可得b1·2k-1=a1+(m-1)d+a1,即b1·2k-1=b1+(m-1)·2b1+b1,得2k-1=2m.∵1≤m≤500,∴2≤2k-1≤1 000.∴2≤k≤10.又k∈Z,故集合{k|bk=am+a1,1≤m≤500}中元素的个数为9.
考点二 数列的奇偶项问题
例2(2023·新高考Ⅱ,18)已知{an}为等差数列,bn= 记Sn,Tn分别为数列{an},{bn}的前n项和,S4=32,T3=16.(1)求{an}的通项公式;(2)证明:当n>5时,Tn>Sn.
(1)解 设等差数列{an}的公差为d.
[对点训练2](2024·山东师大附中模拟)已知{an}是各项均为正数的数列,Sn
(1)求{an}的通项公式;(2)已知bn=(-1)nan,求数列{bn}的前n项和Tn.
(2)由(1)知bn=(-1)n(n+1)2,当n是奇数时,Tn=-22+32-42+52-62+72-…-(n-1)2+n2-(n+1)2=(3-2)×(3+2)+(5-4) ×(5+4)+(7-6)×(7+6)+…+[n-(n-1)](n+n-1)-(n+1)2=5+9+13+…+(2n-1)-(n+1)2
当n是偶数时,Tn=-22+32-42+52-62+72-…-n2+(n+1)2=(3-2)×(3+2)+(5-4) ×(5+4)+(7-6)×(7+6)+…+[(n+1)-n](n+n+1)=5+9+13+…+(2n+1)
考点三 数列与不等式的综合问题(多考向探究预测)
考向1数列中的存在性问题例3(2024·广东中山纪中等六校联考)记Sn为数列{an}的前n项和,已知Sn,2n的等差中项为an.(1)求证:{an+2}为等比数列.(2)数列{ }{的前n项和为Tn,是否存在整数k满足Tn∈(k,k+1)?若存在,求k;否则说明理由.
(1)证明 因为Sn,2n的等差中项为an,所以Sn+2n=2an,因为n=1时,S1=a1,则S1+2=2a1,所以a1=2,由Sn+2n=2an得Sn+1+2n+2=2an+1,又an+1=Sn+1-Sn,所以an+1+2=2an+1-2an,即an+1=2an+2,所以有an+1+2=2(an+2),
所以{an+2}是等比数列,其首项为a1+2=4,公比为2.
所以Tn∈(0,1),所以k=0.
考向2数列中的不等式恒成立问题例4(2021·浙江,20)已知数列{an}的前n项和为Sn,a1= ,且4Sn+1=3Sn-9.(1)求数列{an}的通项公式;(2)设数列{bn}满足3bn+(n-4)an=0(n∈N*),记{bn}的前n项和为Tn,若Tn≤λbn对任意n∈N*恒成立,求实数λ的取值范围.
[对点训练3](2024·河北保定模拟)在数列{an}中,a1= ,2an=an-1-2n-2(n≥2).(1)证明:数列{an+2n}是等比数列;(2)记数列{n(an+2n)}的前n项和为Tn,若关于n的不等式n(2-Tn)≤ 恒成立,求实数λ的取值范围.
考点四 数列与概率的综合问题
例5(12分)(2023·新高考Ⅰ,21)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8,由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.(1)求第2次投篮的人是乙的概率;关键点:第一次谁先投篮不确定.(2)求第i次投篮的人是甲的概率;
突破口:找到甲第i次投篮的概率与第i+1次投篮概率的递推公式.
(3)已知:若随机变量Xi服从两点分布,且P(Xi=1)=1-P(Xi=0)=qi,i=1,2,…,n,则
E(Y).关键点:Xi可取0,1,P(Xi=1)=pi,P(Xi=0)=1-pi,则Xi服从两点分布.审题指导:(1)根据全概率公式求解;(2)设P(Ai)=pi,由题意可得pi+1=0.4pi+0.2,根据数列知识,构造等比数列解决;(3)先求出两点分布的期望,再根据题中的结论以及等比数列的求和公式求解.
规范解答:解(1)记“第i次投篮的人是甲”为事件Ai,“第i次投篮的人是乙”为事件Bi,
(2)设P(Ai)=pi,依题可知P(Bi)=1-pi,
Bi与Ai是对立事件
an+1=pan+q的形式,适合构造等比数列
即pi+1=0.4pi-0.6λ,需-0.6λ=0.2
甲、乙谁第一次投篮是等可能的
适合分组为一个等比数列和一个常数列求和
[对点训练4](12分)(2019·全国Ⅰ,理21)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.(ⅰ)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;(ⅱ)求p4,并根据p4的值解释这种试验方案的合理性.
(2)(ⅰ)由(1)得a=0.4,b=0.5,c=0.1.因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1).又因为p1-p0=p1≠0,
(ⅱ)由(ⅰ)可得p8=p8-p7+p7-p6+…+p1-p0+p0=(p8-p7)+(p7-p6)+…+(p1-p0)
考点五 数列在实际问题中的应用
例6(2024·福建厦门模拟)甲、乙两大超市同时开业,第一年的全年销售额均为1千万元,由于管理经营方式不同,甲超市前n年的总销售额为 千万元,乙超市第n年的销售额比前一年的销售额多 千万元.(1)分别求甲、乙超市第n年销售额的表达式;(2)若其中一家超市的年销售额不足另一家超市的年销售额的50%,则该超市将被另一家超市收购,判断哪一家超市有可能被收购?如果有这种情况,至少会出现在第几年结束时?
适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练43数列中的综合问题课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练43数列中的综合问题课件新人教A版,共24页。
适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练42破解基于问题情境的数列问题课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练42破解基于问题情境的数列问题课件新人教A版,共14页。PPT课件主要包含了答案D,ABD等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练41数列求和课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第6章数列课时规范练41数列求和课件新人教A版,共13页。












