数学七年级下册6.1 平方根教课内容课件ppt

这是一份数学七年级下册6.1 平方根教课内容课件ppt，共17页。PPT课件主要包含了学习目标，复习引入，正数x，概念复习，互为相反数，探究新知，一个数的平方，这个数，∴±3是9的平方根，开平方等内容，欢迎下载使用。

1.了解平方根的概念。2.掌握平方根的特征。3.能利用开平方和平方互为逆运算的关系，求某些非负数的平房根．
问题：4的算数平方根怎么写？
一般地，如果一个_____x的平方等于 a，即 x2=a，那么这个_______叫做 a 的算术平方根.
如果一个数的平方等于9，这个数是多少？
32=9，这个数可以是 3.
（-3）2=9，这个数也可以是 -3.
因此，如果一个数的平方等于9，那么这个数是 3 或 -3.
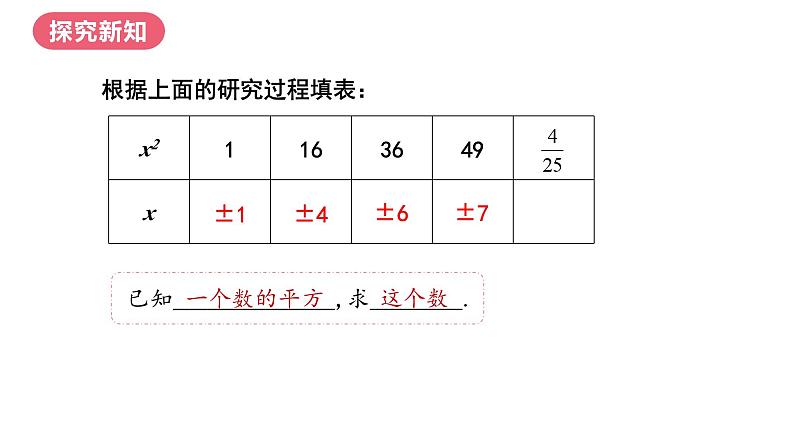
根据上面的研究过程填表：
已知______________,求________.
一般地, 如果一个数的平方等于a, 那么这个数叫做a的平方根或二次方根.
求一个数a的平方根的运算，叫做开平方.
如果我们把±3，±3，±3，±3，±3分别叫做1，16,36,49， 的平方根你能类比算术平方根的概念，给出平方根的概念吗？
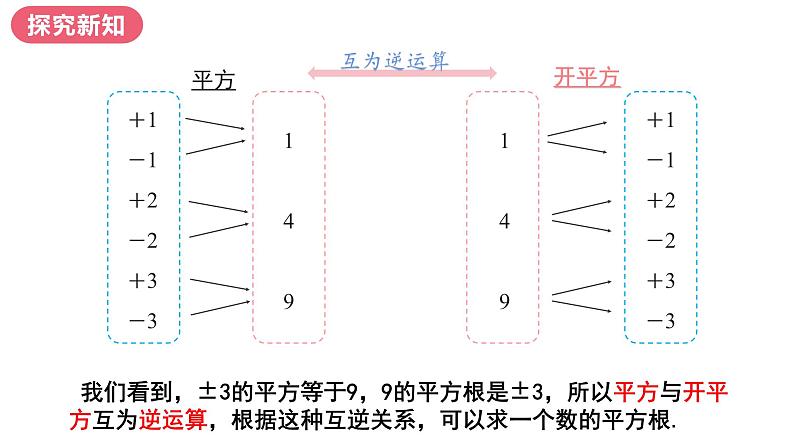
我们看到，±3的平方等于9，9的平方根是±3，所以平方与开平方互为逆运算，根据这种互逆关系，可以求一个数的平方根.
＋1－1＋2－2＋3－3
例 4 求下列各数的平方根：
解：（1）因为（±10）2=100，所以100的平方根是±10；
（3）因为（±0.5）2=0.25，所以0.25的平方根是±0.5.
（4）因为（± ）2= ，所以 的平方根是 .
（5）因为02=0，所以0的平方根是0.
例 4 判断下列说法是否正确，并说明理由：
（1）49的平方根是7
（3）-5是25的平方根
（4）64的平方根是±8
（5）-16的平方根是-4
正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.
根据上题请归纳平方根的特点：
一个正数a的算数平方根可以表示为 那么它的平方根怎么表示了？
即非负数 a 的平方根表示为：
读作“正、负根号 a”.
例5 先说出下列各式的意义，再求下列各式的值： （1） ； （2） ； （3） .
解：（1）因为62=36，所以 ；（2）因为0.92=0.81，所以 ；（3）因为 ，所以 .
练习 1.判断下列各式计算是否正确，并说明理由。
2.说出下列各式的意义，并求他们的值。
求下列各式中 x 的值：(1) 3x2=48； (2) (x+1)2=4； (3) 2(x-1)2-18=0.
(3)原式可变形为 (x-1)2=9. 因为(±3)2=9， 所以 x-1=3 或 x-1=-3，解方程，得x=4 或 x=-2.所以 x=4 或 x=-2.