初中数学北师大版八年级下册3 中心对称评课ppt课件

这是一份初中数学北师大版八年级下册3 中心对称评课ppt课件，共13页。

1.经历观察、操作、欣赏和设计的过程，理解中心对称的定义及性质,并利用中心对称的性质解决实际问题。2.会识别中心对称图形，能利用中心对称图形的性质解决实际问题。
任务一：中心对称的定义及性质
活动1：观察下图，图（1）经过怎样的运动变化就可以与图（2）重合？你还能举出一些类似的例子吗？与同伴交流.
图（1）以一定点旋转180°就可以与图（2）重合.
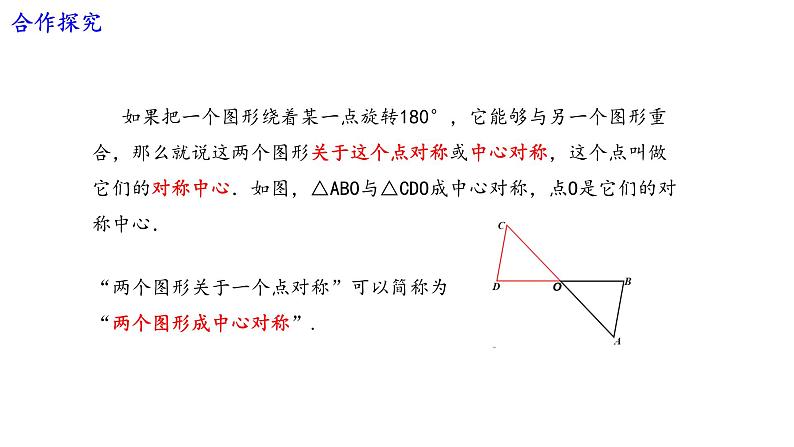
“两个图形关于一个点对称”可以简称为“两个图形成中心对称”.
如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做它们的对称中心．如图，△ABO与△CDO成中心对称，点O是它们的对称中心．
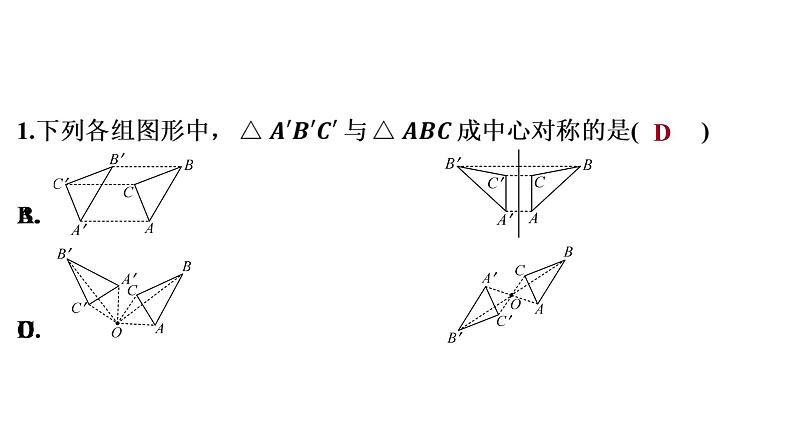
A. &1& B. &2& C. &3& D. &4&
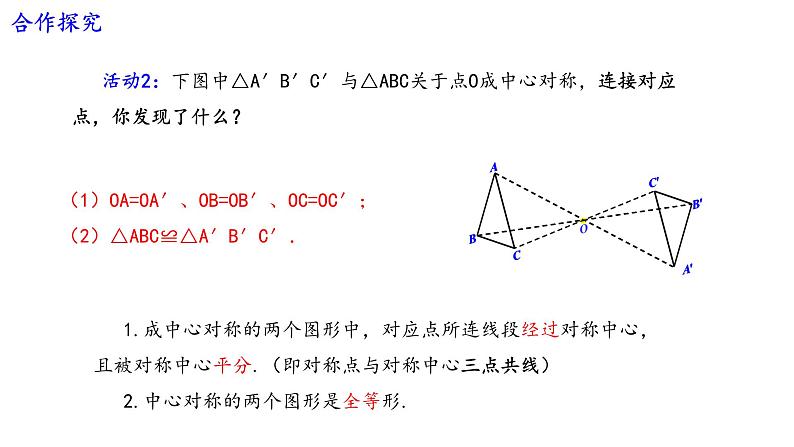
活动2：下图中△A′B′C′与△ABC关于点O成中心对称，连接对应点，你发现了什么？
（1）OA=OA′、OB=OB′、OC=OC′；（2）△ABC≌△A′B′C′．
1.成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分.（即对称点与对称中心三点共线）2.中心对称的两个图形是全等形.
作中心对称图形：如图，已知四边形ABCD和点O，试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
（2）同理，可作出点B，C，D的对应点B'，C'，D'；
（3）顺次连接A'，B'，C'，D'，则四边形A'B'C'D'即为所作.
作法：（1）连接AO并延长到A'，使OA'=OA，得到点A的对应点A'；
逆向思维--找对称中心： 如图，已知△ABC和△A′B′C′成中心对称，画出它们的对称中心．
根据观察，B、B′及C、C′是两组对应点，连结BB′、CC′，BB′、CC′相交于点O，则O为对称中心．如图．
连接C、C′，取CC′中点
关于原点对称的点的坐标
关于非原点对称的点的坐标
观察这些图形，它们有什么共同特征？
把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心.
任务二：中心对称图形的定义
学过的平面图形中，哪些是中心对称图形？
线段、平行四边形、边数为偶数的正多边形、圆
2.（2023·陕西）下列图形中，既是轴对称图形，又是中心对称图形的是( )
A. &5& B. &6& C. &7& D. &8&