




2024年中考数学复习课件---第23讲 与圆有关的位置关系
展开1.探索并掌握点与圆的位置关系.2.了解直线与圆的位置关系,掌握切线的概念.3.了解三角形的内心.4.探索并证明切线长定理:过圆外一点的两条切线长相等.
教材链接人教:九上P92~P104 北师:九下P85~P96 湘教:九下P61~P76
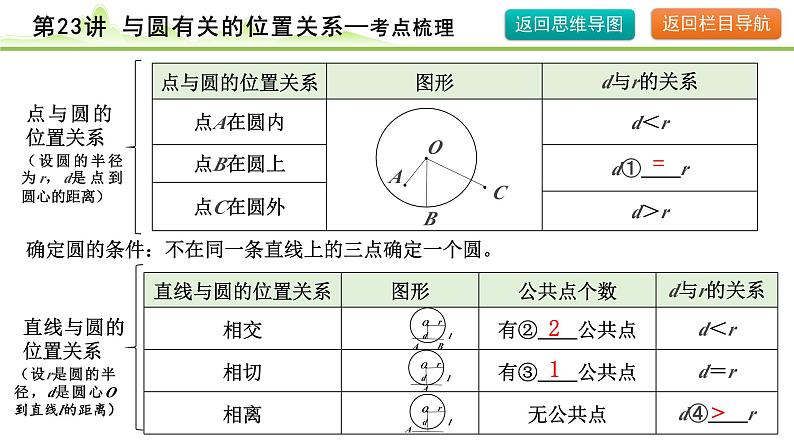
(设圆的半径为r,d是点到圆心的距离)
确定圆的条件:不在同一条直线上的三点确定一个圆。
(设r是圆的半径,d是圆心O到直线l的距离)
定义:经过圆外一点作圆的一条切线,这一点和切点之间 的线段长度叫这点到圆的切线长切线长定理:从圆外一点可以引圆⑧ 条切线,它们的切线长⑨ , 这一点和圆心的连线⑩__ 两条切线的夹角.如图, PA, PB为O的切线,AB为切点,那么 PA=PB,且∠APO=∠BPO.
例 如图,☉O是△ABC的外接圆,AC为直径,点D在半圆AC上, 且与点B在AC的异侧,BE⊥DC交DC的延长线于点E,∠1=∠BCE. (1)求证:BE是☉O的切线;
证明:如图1,连接OB. ∵OC=OB, ∴∠1=∠OBC.∵∠1=∠BCE,∴∠OBC=∠BCE,∴OB∥DC.∵BE⊥DC,∴OB⊥BE.∵OB是☉O的半径,∴BE是☉O的切线.
(3)BE交AC的延长线于点F,G是OA的中点,过G作GH⊥AC,交EB的延长线于点H.求证:∠H=2∠BAC.
解:如图2.∵BE是☉O的切线,GH⊥AC,∴△OBF和△FHG都是直角三角形.∵∠F=∠F,∴∠BOF=∠H.又∵∠BOF=2∠BAC,∴∠H=2∠BAC.
②cs∠DBA= ;
(2)若EC=1,CD=4. ①BC的长为 ;
已知圆的切线:1.求线段长时,常连接切点与圆心,构造直角三角形,然后利用锐角三角函数或勾股定理或相似三角形求解.2.求角的度数时,连接切点与圆心构造直角三角形,结合圆周角定理及其推论、三角形内角和定理及平行线的性质等解决问题.
1.(2022·遵义红花岗区二模)如图,在Rt△ABC中,∠C=90°,AB=20, BC=12,点O为边AC上的一点,以点O为圆心,半径为6作半圆O,与AC 交于点D.
(1)如图1,BC与半圆O相切时,求证:AB与半圆O相切;
(2)如图2,点O为AC的中点时,将线段CD连同半圆O绕点C旋转.若半圆O与Rt△ABC的直角边相切,设切点为K,连接AK,求AK的长.
2.(2022·贵阳观山湖区模拟)如图,PA是☉O的切线,切点为A,AC是 ☉O的直径,连接OP交☉O于点E.过A点作AB⊥PO于点D,交☉O于 点B,连接BC,PB.
(1)求证:PB是☉O的切线;
(2)求证:E为△PAB的内心;
证明:如图,连接AE.∵PA为☉O的切线,∴∠PAE+∠OAE=90°.∵AD⊥ED,∴∠EAD+∠AED=90°.∵OE=OA,∴∠OAE=∠AED.∴∠PAE=∠EAD,即AE平分∠PAD.∵PA,PB为☉O的切线,∴PD平分∠APB.∴E为△PAB的内心.
(2017~2022)
1.(2017·黔南州10题4分)如图,已知直线AD是☉O的切线,点A为切点,OD 交☉O于点B,点C在☉O上,且∠ODA=36°,则∠ACB的度数为( )
与切线的性质有关的计算(贵阳6年4考,毕节6年2考,遵义6年2考)
A.54° B.36° C.30° D.27°
2.(2022·黔东南州8题·4分)如图,PA,PB分别与☉O相切于点A,B,连 接PO并延长与☉O交于点C,D,若CD=12,PA=8,则sin∠ADB的值 ( )
3.(2022·黔东南州23题14分)(1)请在图1中作出△ABC的外接圆☉O(尺 规作图,保留作图痕迹,不写作法);
解:如图1,☉O即为△ABC的外接圆;
4.(2022·铜仁22题10分)如图,D是以AB为直径的☉O上一点,过点D的 切线DE交AB的延长线于点E,过点B作BC⊥DE交AD的延长线于点C, 垂足为F. (1)求证:AB=CB;
证明:连接OD,如图1,∵DE是☉O的切线,∴OD⊥DE.∵BC⊥DE,∴OD∥BC.∴∠ODA=∠C.∵OA=OD,∴∠ODA=∠A.∴∠A=∠C.∴AB=BC;
5.(2019·贵阳23题10分)如图,已知AB是☉O的直径,点P是☉O上一点, 连接OP,点A关于OP的对称点C恰好落在☉O上. (1)求证:OP∥BC;
解:如图,连接PC. ∵CD为☉O的切线,∴OC⊥CD.又∵AD⊥CD,∴OC∥AD.∴∠APO=∠COP.∵∠AOP=∠COP,∴∠APO=∠AOP.∴OA=AP.∵OA=OP,∴△APO为等边三角形. ∴∠APO=∠AOP=60°=∠COP.又∵PO=CO,∴△POC等边三角形.∴PC=PO,∠OPC=60°,∴∠DPC=60°.∵∠D=90°,∴∠PCD=30°.在Rt△PCD中,PC=2PD=2=PO,∴AB=2PO=4.
(2)过点C作☉O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求☉O的直径.
6.(2020·贵阳23题10分)如图,AB为☉O的直径,四边形ABCD内接于 ☉O,对角线AC,BD交于点E,☉O的切线AF交BD的延长线于点F,切点 为A,且∠CAD=∠ABD. (1)求证:AD=CD;
证明:∵∠CAD=∠ABD,∠ABD=∠ACD∴∠ACD=∠CAD.∴AD=CD.
(2)若AB=4,BF=5,求sin∠BDC的值.
与切线的判定有关的证明和计算(遵义6年2考,毕节6年3考)
(2)若BD=2,OB=4,求tan∠AFC的值.
证明:如图,连接OD. ∵AB是直径,∴∠ACB=90°.∵DE∥BC,∴∠E=∠ACB=90°.∵OA=OD,∴∠OAD=∠ADO.∵AD平分∠CAB,∴∠DAE=∠OAD.∴∠ADO=∠DAE.∴OD∥AE.∴∠ODE=180°-∠E=90°,即OD⊥DE.∴DE是☉O的切线.
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
9.(2021·铜仁24题12分)如图,已知△ABC内接于☉O,AB是☉O的直径, ∠CAB的平分线交BC于点D,交☉O于点E,连接EB,作∠BEF=∠CAE, 交AB的延长线于点F. (1)求证:EF是☉O的切线;
证明:如图,连接OE. ∵AB是☉O的直径,∴∠AEB=90°,即∠AEO+∠OEB=90°.∵AE平分∠CAB,∴∠CAE=∠BAE.∵∠BEF=∠CAE,∴∠BEF=∠BAE.∵OA=OE,∴∠BAE=∠AEO.∴∠BEF=∠AEO.∴∠BEF+∠OEB=90°,即∠OEF=90°.∴OE⊥EF.∵OE是☉O的半径,∴EF是☉O的切线.
(2)若BF=10,EF=20,求☉O的半径和AD的长.
10.(2022·黔西南州23题12分)如图,在△ABC中,AB=AC,以AB为直径作 ☉O,分别交BC于点D,交AC于点E,DH⊥AC,垂足为H,连接DE并延长 交BA的延长线于点F. (1)求证:DH是☉O的切线;
证明:如图所示,连接OD, ∵OB=OD,∴∠OBD=∠ODB.∵AB=AC,∴∠ABC=∠ACB.∴∠ODB=∠ACB.∴OD∥AC.∵DH⊥AC,∴DH⊥OD.∵OD是☉O的半径,∴DH是☉O的切线;
初中数学中考复习 第29讲 与圆有关的位置关系课件PPT: 这是一份初中数学中考复习 第29讲 与圆有关的位置关系课件PPT,共36页。PPT课件主要包含了或256等内容,欢迎下载使用。
初中数学中考复习 第29讲 与圆有关的位置关系课件PPT: 这是一份初中数学中考复习 第29讲 与圆有关的位置关系课件PPT,共30页。PPT课件主要包含了垂直于,①②④,不在同一直线上的,垂直平分线,角平分线,各个顶点等内容,欢迎下载使用。
中考数学复习第22讲与圆有关的位置关系精练课件: 这是一份中考数学复习第22讲与圆有关的位置关系精练课件,共20页。












