2022年广西桂林中考数学复习课件：第22讲 与圆有关的位置关系

这是一份2022年广西桂林中考数学复习课件：第22讲 与圆有关的位置关系，共26页。PPT课件主要包含了知识清单·理脉络，d＞r，d＝r，d＜r，垂直平分线，三个顶点，垂直于，内切圆，角平分线，高频考点·释疑难等内容，欢迎下载使用。

一、点与圆的位置关系1．设圆O的半径为r，点P到圆心的距离为OP＝d.则：点P在圆外⇔________；点P在圆上⇔________；点P在圆内⇔________．2．确定圆的条件：不在同一直线上的三个点确定________圆．3．三角形的外心：三角形外接圆的圆心，三角形三边的_____________的交点．外心到三角形____________的距离相等．
二、直线与圆的位置关系1．三种位置关系：________、________、________．2．切线的定义、性质与判定：(1)定义：和圆有________公共点的直线．(2)性质：圆的切线__________过切点的直径．(3)判定：经过半径的外端，并且________于这条半径的直线是圆的切线．3．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长________，这一点和圆心的连线________两条切线的夹角．
三、三角形的内切圆与外接圆1．三角形的内切圆(1)定义：与三角形各边都____的圆．(2)三角形的内心：三角形______的圆心，是三角形三条________的交点．内心到三角形____的距离相等．2．三角形的外接圆(1)定义：经过三角形的三个____可以作一个圆，这个圆叫三角形的外接圆．(2)三角形的外心：三角形外接圆的圆心，是三角形三边的_________的交点．
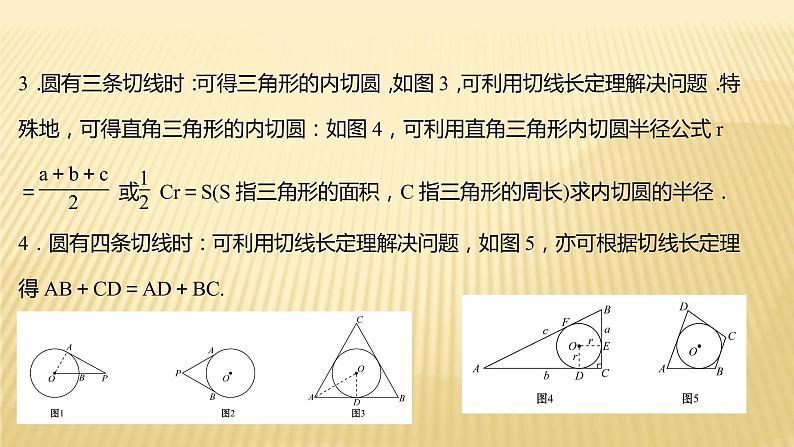
四、切线的性质及基本图形模型1．圆有一条切线时：在圆中，若有切线，则“连接圆心和切点”是最常见的作辅助线的方法．可应用切线的性质证明线段相等，角相等或进行有关计算．如图1，点P为⊙O外一点，PA为⊙O的切线，A为切点，则OA⊥PA.2．圆有两条切线时：可应用切线长定理：如图2，若PA，PB是⊙O的两条切线，则PA＝PB.
五、切线的判定：方法一：有交点，连半径，证垂直；方法二：无交点，作垂直，证半径．
【自我诊断】(打“√”或“×”)1．线段OP＝5，则点P在以O为圆心，3为半径的圆的外部．( )2．三点确定一个圆．( )3．三角形的外心一定在三角形外部．( )4．三角形的外心到三角形三边的距离相等．( )5．一条直线和圆最多有两个公共点．( )6．⊙O的半径为5，P为直线l上一点，且OP＝6，则直线l与⊙O相离．( )7．切线长就是圆的切线的长度．( )8．三角形的内心到三角形三个顶点的距离相等．( )
【答题关键指导】直线与圆的三种位置关系设圆的半径为r，圆心到直线的距离为d.(1)直线与圆相交⇔dr.
【思路点拨】(1)连接OD，根据已知条件可推出△DOA是等边三角形，利用∠ODA＝∠C即可证明OD∥BC，进而可知∠DFC＝∠ODF＝90°，即可求证；(2)用含有a和r的式子分别表示出BE和BF的长，根据BF＝2BE列出等式即可找到r与a的数量关系．
【答题关键指导】关于切线长定理图形的应用如图，PA，PB是⊙O的两条切线，OA⊥PA，OB⊥PB，1.证线段相等 如：PA＝PB，OA＝OB，AC＝BC…2．证角相等如：∠APO＝∠BPO，∠PAB＝∠PBA，∠OAB＝∠OBA，∠AOP＝∠BOP…3．证垂直关系 如：PA⊥OA，PB⊥OB，OP⊥AB…
(2)(2021·襄阳中考)点O是△ABC的外心，若∠BOC＝110°，则∠BAC为_____________．
【答题关键指导】三角形外心的性质1．三角形的外心是外接圆的圆心，它是三角形三边垂直平分线的交点，它到三角形三个顶点的距离相等．2．三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合．3．三角形的内心是三角形内切圆的圆心，它是三角形三个内角平分线的交点，它到三角形三边的距离相等．4．一个三角形只有一个内切圆，但一个圆有无数个外切的三角形．