专题五 圆课件---2024年中考数学一轮复习

这是一份专题五 圆课件---2024年中考数学一轮复习，共46页。PPT课件主要包含了类型清单，题型讲解，方法点拨，解题技巧，例题1，思路指导，当堂检测，例题2，例题3等内容，欢迎下载使用。

静态圆型问题是以圆为背景,与平行线、三角形、四边形、函数、方程等知识结合,考查圆的有关性质、垂径定理、切线的性质、扇形的计算等内容.圆可构成内容丰富、题型新颖、构思精巧的综合性试题,考查的题型主要是以计算题和证明题的形式出现,培养了学生的几何直观和空间观念的核心素养.
解决静态圆型问题需要熟练掌握弦、弧、圆心角三者之间关系并能灵活转化,运用三角形全等、相似三角形、锐角三角函数、勾股定理等知识进行证明与计算.解题时需要先分析题目中的已知条件,再观察图形,从中挖掘出隐含条件,最后综合分析信息解决问题.
以圆为背景的证明与计算题,利用半径构造等腰三角形,利用直径构造直角三角形,从圆心角或圆周角看弧、从弧找角进行等角转移,经常作为隐含条件.最常用的辅助线:作弦心距、作过切点的半径.
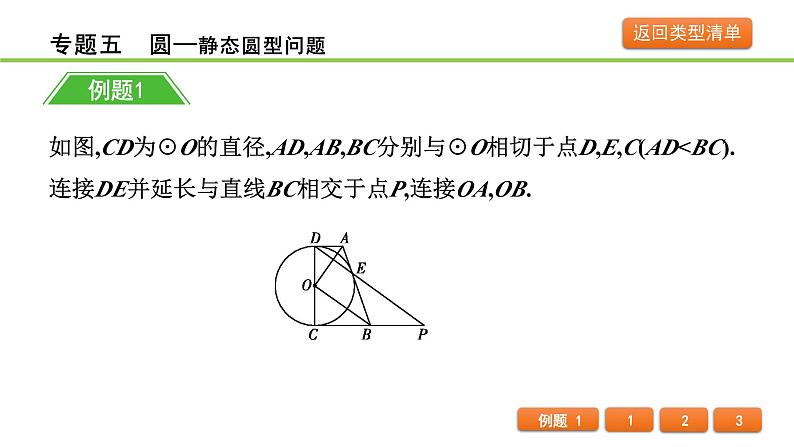
如图,CD为☉O的直径,AD,AB,BC分别与☉O相切于点D,E,C(AD (1)求证:OA⊥OB;
(1)连接OE,根据切线长定理及切线的性质可得OD⊥AD,OE⊥AB,OC⊥BC,即可得出点A在∠DOE的平分线上,点B在∠COE的平分线上,根据平角的定义即可得结论;
(2)连接CE,根据等腰三角形的性质、直径所对圆周角是直角,即可证明∠P=∠PEB,可得BE=BP,即可得出BC=PB;
(2)求证:BC=BP;
(3)若OA=3,OB=4,求AD·BC的值.
2.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的圆O分别交AB,AC于点E,F,连接EF.
(1)求证:BC是圆O的切线;
(2)证明:如图2,连接DF,∵AE是圆O的直径,∴∠AFE=90°,∴∠AFE=∠C=90°,∴EF∥BC,∴∠AEF=∠B.∵∠AEF=∠ADF,∴∠B=∠ADF.又∵∠BAD=∠CAD,∴△ABD∽△ADF,∴AB:AD=AD:AF,∴AD2=AF·AB.
(2)求证:AD2=AF·AB;
3.(2022·河北一模)如图,已知A,B,C分别是☉O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与☉O相切;
(2)如果AC=3,求PD的长.
动态圆型问题是关于圆知识考查的热点类型,常以综合题的形式出现,涉及解直角三角形、四边形、函数基本性质、直线与圆的位置关系、圆的切线的性质、图形变换等知识,解题的关键是灵活运用数形结合、分类讨论、转化等数学思想思考问题.
动态圆型问题要用运动的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住其中的数量关系,并特别关注一些特别的量、不变的关系或特殊关系,善于化动为静,由特殊情形(特殊点、特殊位置、特殊值、特殊图形)逐步过渡到一般情形,再综合运用各种相关的数学知识、数学思想加以解决.
画出符合题意的示意图,分析运动过程,先定临界状态,再定范围;建构三角形(直角三角形)或特殊四边形,并利用其性质解决问题.
(2022·石家庄桥西区模拟)已知,矩形ABCD中,AB=6,AD=8,O为对角线BD的中点,P为AD上一点,连接PO,以O为圆心,OP为半径画圆O. (1)如图①,当点P为AD中点时,圆O与AD的位置关系为　　　　,OP的长为　　　　; 
(1)利用三角形中位线性质和切线的判定定理得出答案;
模型一 圆心不动,半径变化
(2)如图②,当圆O与AB相切,且AP＜PD时,求PD的长;
(2)连接经过切点的半径,过点O作AD的垂线,利用三角形的中位线和勾股定理,可以求出PD的长;
(3)延长BA到E,使得AE=AB,连接DE,当圆O与△BDE有4个交点时,直接写出圆O的半径r的取值范围.
(3)分情况讨论,利用临界状态,求出特殊值,即可求出r的取值范围.
4.(原创题)已知:在平面直角坐标系xOy中,△ABC的顶点均在坐标轴上,且A(-3,0),点B(0,4),点C在x轴正半轴上,且AC=10,点P从点C出发,沿着射线CA方向以2个单位长度/s的速度匀速运动,以点C为圆心,CP为半径作☉C.
(1)求直线AB的表达式;
(2)若☉C与直线AB相切,求点P的运动时间t(s)的值;
(3)若☉C与线段AB有交点,求点P的运动时间t(s)的取值范围.
(1)求k的值及点N的坐标;
(2)若☉P与线段MN有公共点,试求☉P半径r的取值范围.
模型二 圆心在动,半径不变
6.如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的☉P与△ABC的一边相切时,AP的长为　　　　　　. 
7.(2022·邯郸武安一模)如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12 cm,半圆O的直径DE=12 cm,点E与点C重合,半圆O以2 cm/s的速度从左向右移动,在运动过程中,点D,E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分面积为S(cm2).
(1)当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN最大为　　　　 cm;MN最小为　　　　 cm. (2)在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S.
(3)当x为何值时,半圆O与△ABC的边所在的直线相切?请直接写出结果.