

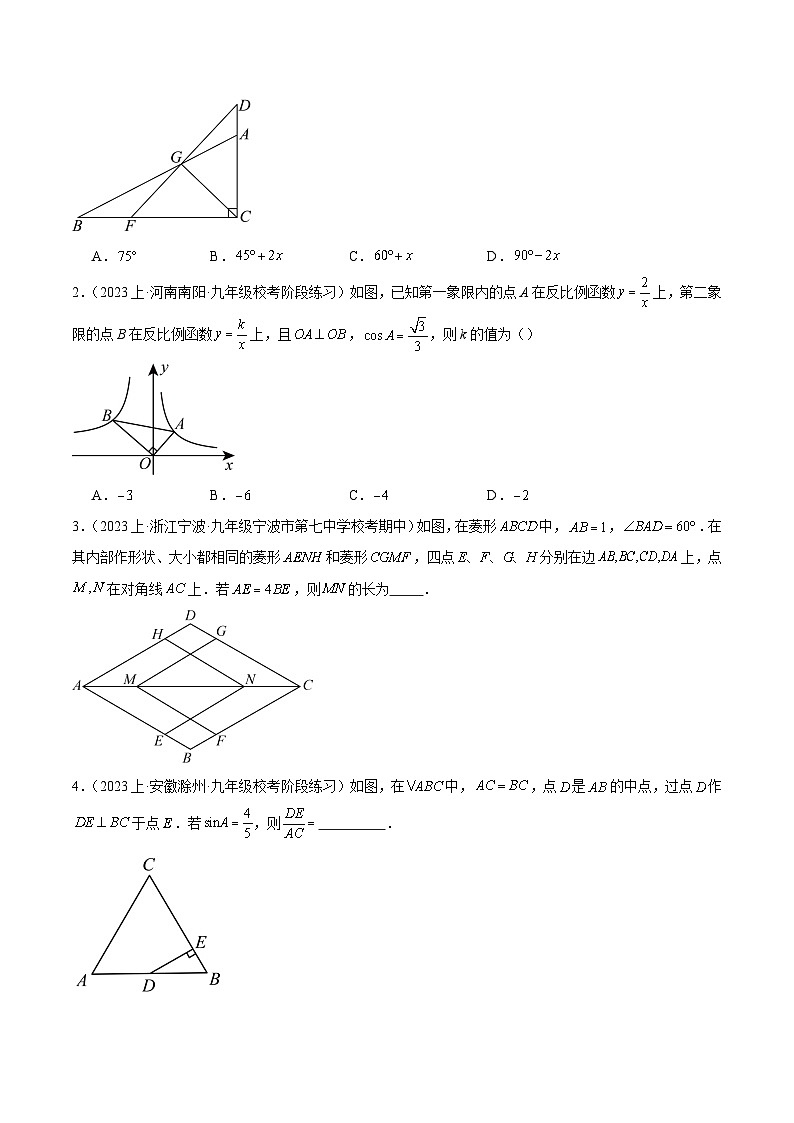



- 专题03 解直角三角形及其应用(7大题型)-2023-2024学年九年级数学下册重难点高分突破(浙教版) 试卷 0 次下载
- 第1章 解直角三角形 重难点检测卷-2023-2024学年九年级数学下册重难点高分突破(浙教版) 试卷 0 次下载
- 期中押题重难点检测卷(基础卷)(考试范围:第1-4章)-2023-2024学年九年级数学上册重难点高分突破(浙教版) 试卷 0 次下载
- 期中押题重难点检测卷(提高卷)(考试范围:第1-4章)-2023-2024学年九年级数学上册重难点高分突破(浙教版) 试卷 0 次下载
- 期末重难点真题特训之易错必刷题型(浙教版上册)(92题23个考点)-2023-2024学年九年级数学上册重难点高分突破(浙教版) 试卷 0 次下载
期末重难点真题特训之易错必刷题型(浙教版九下)(55题11个考点)-2023-2024学年九年级数学下册重难点高分突破(浙教版)
展开易错必刷题一、锐角三角函数
1.(2023上·广西梧州·九年级校考阶段练习)在中,已知,那么下列结论正确的是( )
A.B.C.D.
2.(2023上·河北邢台·九年级统考阶段练习)在中,是的中线,则的值是( )
A.B.C.D.
3.(2023上·辽宁沈阳·九年级沈阳市实验学校校联考期中)在中,,,点D是边上一点,,,则 .
4.(2023上·河南郑州·九年级校考阶段练习)如图,在等腰中,,,点D为的中点,于点E,则的值为 .
5.(2023上·安徽亳州·九年级校联考期末)如图,是正方形的对角线,平分交于,点在上,且,连接并延长,分别交,于点G,F.
(1)求证:;
(2)求的值;
(3)求的值.
易错必刷题二、锐角三角函数的计算
1.(2023上·天津·九年级校考阶段练习)计算的结果是( )
A.B.C.D.
2.(2024上·福建莆田·九年级校考阶段练习)在中,若角,满足,则的大小是( )
A.B.C.D.
3.(2023上·安徽亳州·九年级校联考阶段练习)在中,,都是锐角,且,则是 三角形.
4.(2023上·山东淄博·九年级校考阶段练习)已知为锐角,,则 .
5(2023上·甘肃天水·九年级校考阶段练习)计算:
(1);
(2).
易错必刷题三、解直角三角形
1.(2023上·重庆沙坪坝·九年级重庆八中校考期中)如图,在中,,,为线段延长线一点,为线段上一点,连接交于点,连接,若,设,则可表示为( )
A.B.C.D.
2.(2023上·河南南阳·九年级校考阶段练习)如图,已知第一象限内的点A在反比例函数上,第二象限的点B在反比例函数上,且,,则k的值为()
A.B.C.D.
3.(2023上·浙江宁波·九年级宁波市第七中学校考期中)如图,在菱形中,,.在其内部作形状、大小都相同的菱形和菱形,四点分别在边上,点在对角线上.若,则的长为 .
4.(2023上·安徽滁州·九年级校考阶段练习)如图,在中,,点是的中点,过点作于点.若,则 .
5.(2023上·陕西咸阳·九年级校考期中)如图,在平行四边形中,、相交于点O,且,过点A作,过点C作于点E,延长交于点H,交于点F,且,连接、.
(1)求证:四边形是矩形;
(2)试判断四边形的形状,并说明理由;
(3)若,,,求的长.
易错必刷题四、解直角三角形的应用
1、(2023上·浙江温州·九年级校考阶段练习)利用投影灯测量计算坡比.如图,投影灯的下边缘光线落在坡脚点B处,上边缘光线落在斜坡点C处,此时投影灯O离地面距离为1.5m,离坡角B点水平距离为5m.将投影灯往上平移,上下边缘的光线,,恰好落在斜坡D,C处,此时投影灯向上平移了0.9米,现测得,则斜坡的坡比为( )
A.B.C.D.
2.(2023上·山西长治·九年级校联考期末)学校摄影兴趣小组在上摄影课,小王发现摄影三脚架如图1所示,该支架三个脚长度相同且与地面夹角相同.如图2,过点A向地面作垂线,垂足为C.若三脚架的一个脚的长为2米,,则相机距地面的高度为( )
A.米B.米C.米D.米
3.(2023上·河北石家庄·九年级校考阶段练习)北斗卫星导航系统是中国自行硏制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶10千米至B地,再沿北偏东60°方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.则的度数为 ;B、C两地的距离是 .(结果保留根号)
4.(2023上·浙江温州·九年级温州绣山中学校考阶段练习)如图,将的按下面的方式放置在一把刻度尺上,定点与刻度尺下边沿的端点重合,与刻度尺下边沿重合,与刻度尺上边沿的交点在刻度尺上的读数恰为.若将射线绕点O顺时针旋转与尺子的上沿交于点C,则点C在刻度尺上的读数约为 (结果精确到,参考数据:,,).
5.(2023上·四川成都·九年级校考期中)第31届世界大学生运动会于2023年7月28日在成都举行,主火炬塔位于东安湖体育公园,亮灯之夜,塔身通体透亮,10余道象征太阳光芒的螺旋线全部点亮,璀璨绚丽,流光溢彩(如图1).小杰同学想要通过测量及计算了解火炬塔的大致高度,当他步行至点处,测得此时塔顶的仰角为,再步行20米至点处,测得此时塔顶的仰角为(如图2所示,点在同一条直线上),请帮小杰计算火炬塔的高.(,,,,,,结果保留整数)
易错必刷题五、直线与圆的位置关系
1.(2023上·河南商丘·九年级校考阶段练习)如图所示,是的切线,A、B为切点,,点C是上不同于A、B的任意一点,则的度数为( )
A.B.C.或D.或
2.(2024上·北京海淀·九年级首都师范大学附属中学校考阶段练习)如图,已知分别与相切于点,为优弧上一点,,则等于( )
A.B.C.D.
3.(2013上·江苏南通·九年级统考期中)如图,在中,,,,则的内切圆半径 .
4.(2023上·江苏无锡·九年级校考阶段练习)如图,在中,,,,点E在中线上,以E为圆心的圆E分别与、相切,则的半径是 .
5.(2023上·浙江宁波·九年级校考期中)如图,是的外接圆,为直径,,,交的延长线于点.
(1)求证:.
(2)求证:是⊙O的切线.
(3)若,求.
易错必刷题六、切线长定理
1.(2023上·河北邢台·九年级校考阶段练习)如图,的圆心在梯形的底边上,且与梯形的其他三边均相切,若,,则梯形的周长为( )
A.8B.10C.14D.18
2.(2023上·山东聊城·九年级校联考阶段练习)如图,中,,内切于点,,,则的半径为( )
A.B.C.D.
3.(2023上·广西南宁·九年级校考阶段练习)如图,在正方形中,以为直径作半圆O,以点D为圆心、为半径作圆弧交半圆O于点P.连接并延长交于点E,则的值为 .
4.(2022上·广东东莞·九年级东莞中学南城学校校考期末)如图:、是的两条切线,、是切点,、是上两点,如果,,则的度数是 度.
5.(2023上·江苏无锡·九年级校考阶段练习)如图,已知P为圆O外一点,,为的切线,切点为A、B,是直径,
(1)说明;
(2)若,,求长.
易错必刷题七、三角形的内切圆
1.(2023上·江苏无锡·九年级江苏省锡山高级中学实验学校校考期中)在下列命题中,正确的是( )
A.任何三角形有且只有一个内切圆
B.三点确定一个圆
C.三角形的内心到三角形的三个顶点的距离相等
D.垂直于半径的直线一定是这个圆的切线
2.(2021·全国·九年级专题练习)如图,的半径为2,圆心M的坐标为,点P是上的任意一点,,且、与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最小值( )
A.3B.4C.5D.6
3.(2023上·浙江宁波·九年级校考期中)如图,在中,,,,是的内切圆,连接,则图中阴影部分的面积之和为 .
4.(2023上·江苏无锡·九年级校考阶段练习)如图,内切于,切点为,已知,则的度数= ;
5.(2023上·浙江嘉兴·九年级校联考期中)如图,为的直径,点都在上,且平分,交于点.
(1)请判断的形状,并说明理由.
(2)若,求的半径;
(3)于点,试探究线段之间的数量关系,并说明理由.
易错必刷题八、投影
1.(2023上·陕西汉中·九年级校联考阶段练习)下列投影,属于平行投影的是( )
A.晚上路灯下小孩的影子B.阳光下沙滩上人的影子
C.汽车灯光照射下行人的影子D.皮影戏中的影子
2.(2023上·浙江温州·九年级温州绣山中学校考阶段练习)兴趣小组测量学校的旗杆,在阳光下,甲同学测得长1米的竹竿影长为米,同一时刻乙同学测量时发现旗杆的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,墙壁垂直地面,如图所示,落在墙上的影长为2米,,落在地面上的影长AB为9米,则旗杆的高度是( )米.
A.8B.12C.D.
3.(2023上·四川成都·九年级校考阶段练习)如图,数学兴趣小组下午测得一根长为的竹竿影长是,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高,地面上的影长为.请你帮算一下,树高是 .
4.(2023上·黑龙江哈尔滨·九年级统考期末)中午12点,身高的小冰的影长为,同学小明此时在同一地点的影长为,那么小明的身高为 .
5.(2023上·江西九江·九年级校考阶段练习)如图,身高的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度.具体做法如下:先从路灯底部向东走25步到M处,发现自己的影子端点刚好在两盏路灯的中间点P处,然后继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
(1)根据题意画图,找出路灯的位置.
(2)通过计算估计路灯的高.
易错必刷题九、简单几何体的三视图
1.(2022·福建泉州·统考模拟预测)如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
A.B.
C. D.
2.(2023下·河南新乡·九年级校联考开学考试)如图是由6个相同的小正方体组成的几何体,下列说法正确的是( )
A.主视图和俯视图一样B.主视图和左视图一样
C.左视图和俯视图一样D.主视图,左视图,俯视图都不一样
3.(2021上·辽宁沈阳·七年级统考期末)如图,5个完全相同的小正方体组成了一个几何体,请在方格纸中用实线画出从正面、左面、上面看到的这个几何体的形状图.
4.(2023上·七年级单元测试)老师用10个的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边()共享,或有一面()共享.老师拿出一张的方格纸(如图②),请小荣将此10个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有 种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
5.(2023上·广东茂名·七年级校联考阶段练习)画出下面由11个小正方体搭成的几何体从不同角度看得到的图形.
(1)请画出从正面看、从左面看、从上面看的平面图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同,请画出添加正方体后,从上面看这个新组合体时看到的一种图形.
易错必刷题十、由三视图描述几何体
1.(2023上·全国·九年级专题练习)一个几何体的主视图和俯视图如图所示,若这个几何体最多由a个小正方体组成,最少由b个小正方体组成,则等于( )
A.10B.11C.12
2.(2023上·陕西西安·七年级陕西师大附中校考阶段练习)某社区的志愿者收到一批防疫物资,这批防疫物资用同样的正方体箱子包装,摆放的位置从上面和正面看到的都是如图所示,这批防疫物资最多有( )箱.
A.6B.7C.8D.9
3.(2023上·安徽宿州·九年级校考阶段练习)一个几何体由13个大小相同的小立方块搭成.这个几何体的三视图如图所示,则这个几何体的搭法共有 种(三视图中没有空白部分).
4.(2023上·内蒙古包头·九年级校考期中)如图是一个几何体的三视图,俯视图是菱形,根据图中数据(单位:),可求得它的体积是 .
5.(2023上·河南郑州·七年级校考期中)如图,是由大小相同的小立方块搭成的几何体,小立方块棱长均为1.
(1)请在方格中分别画出从上面、左面看到该几何体的形状图;
(2)用小立方块搭一几何体,使得从上面、左面看到该几何体的形状图与你在方格中所画一致,则这样的几何体最少要______个小立方块,最多要______个小立方块.
易错必刷题十一、简单几何体的表面展开图
1.(2023上·河北石家庄·九年级校联考期中)如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若,则该圆锥底面半径为( )
A.B.C.1D.2
2.(2023上·河南周口·九年级统考阶段练习)如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为,侧面积为,则这个扇形的圆心角的度数是( )
A.B.C.D.
3.(2023上·河北邢台·九年级统考阶段练习)已知一个扇形的圆心角是,半径是.
(1)这个扇形的弧长是 ;
(2)若用这个扇形围成一个圆锥的侧面,则这个圆锥的高是 .
4.(2023·全国·九年级专题练习)现有一个圆周的扇形纸片,该扇形的半径为,小琪同学为了在“六一”儿童节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作一个底面半径为的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角度数为 .
5.(2023上·安徽阜阳·九年级统考阶段练习)图1中的冰激凌的外包装可以视为圆锥(如图2),制作这种外包装需要用如图3所示的等腰三角形材料,其中,将扇形围成圆锥时,恰好重合.已知这种加工材料的顶角,圆锥底面圆的直径为.
(1)求图2中圆锥的母线的长.
(2)求加工材料剩余部分(图3中阴影部分)的面积.(结果保留)
人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(三)之易错必刷题型专训(原卷版+解析): 这是一份人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(三)之易错必刷题型专训(原卷版+解析),共106页。
专题11 垂径定理重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题11 垂径定理重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题11垂径定理重难点题型专训八大题型原卷版docx、专题11垂径定理重难点题型专训八大题型解析版docx等2份试卷配套教学资源,其中试卷共85页, 欢迎下载使用。
专题09 圆重难点题型专训(十大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题09 圆重难点题型专训(十大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题09圆重难点题型专训十大题型原卷版docx、专题09圆重难点题型专训十大题型解析版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。












