




专题08 选择压轴题精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版)
展开1.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( )
A.23+2B.5−33C.3−3D.3+1
试题分析:方法一:如图,延长DA、BC交于点G,利用正方形性质和等边三角形性质可得:∠BAG=90°,AB=2,∠ABC=60°,运用解直角三角形可得AG=23,DG=2+23,再求得∠G=30°,根据直角三角形性质得出答案.
方法二:过点E作EG⊥DF于点G,作EH⊥BC于点H,利用解直角三角形可得EH=1,BH=3,再证明△BEH≌△DEG,可得DG=BH=3,即可求得答案.
答案详解:解:如图,延长DA、BC交于点G,
∵四边形ABED是正方形,
∴∠BAD=90°,AD=AB,
∴∠BAG=180°﹣90°=90°,
∵△ABC是边长为2的等边三角形,
∴AB=2,∠ABC=60°,
∴AG=AB•tan∠ABC=2×tan60°=23,
∴DG=AD+AG=2+23,
∵∠G=90°﹣60°=30°,DF⊥BC,
∴DF=12DG=12×(2+23)=1+3,
所以选D.
2.已知下列命题
①一组对边平行且相等的四边形是平行四边形;
②两条对角线互相垂直且相等的四边形是正方形;
③一组对边平行且两条对角线相等的四边形是矩形;
④两条对角线互相垂直的平行四边形是菱形.
其中正确的命题的个数是( )
A.0B.1C.2D.3
试题分析:(1)本题根据平行四边形的判定方法即可得出结论.
(2)本题根据对角线互相平分的四边形是平行四边形.
(3)本题根据矩形的判定方法得出结论.
(4)本题根据菱形的判定方法得出结论.
答案详解:解:(1)∵一组对边平行且相等的四边形是平行四边形;
∴故本选项正确.
(2)∵两条对角线互相垂直且相等的四边形不一定是平行四边形,
∴故本选项错误.
(3)∵一组对边平行且两条对角线相等的四边形可能是等腰梯形.
∴故本选项错误.
④∵两条对角线互相垂直的平行四边形是菱形.
∴故本选项正确.
所以选:C.
3.如图,点A是反比例函数y=4x图象上的一动点,连接AO并延长交图象的另一支于点B.在点A的运动过程中,若存在点C(m,n),使得AC⊥BC,AC=BC,则m,n满足( )
A.mn=﹣2B.mn=﹣4C.n=﹣2mD.n=﹣4m
试题分析:连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,根据等腰直角三角形的性质得出OC=OA,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE≌△COF,根据全等三角形的性质,可得出A(n,﹣m),进而得到﹣mn=4,进一步得到mn=﹣4.
答案详解:解:如图,连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,
∵由直线AB与反比例函数y=4x的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC⊥BC,AC=BC,
∴CO⊥AB,CO=12AB=OA,
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE≌△COF(AAS),
∴OE=OF,AE=CF,
∵点C(m,n),
∴CF=﹣m,OF=n,
∴OE=n,AE=﹣m,
∴A(n,﹣m),
∵点A是反比例函数y=4x图象上,
∴﹣mn=4,即mn=﹣4,
所以选:B.
4.在平面直角坐标系中,反比例函数y=kx的图象经过点A(x1,y1),B(x2,y2)(x1≠x2),则下列说法错误的是( )
A.若x1x2<0,则y1y2<0
B.若(x1﹣x2)(y1﹣y2)<0,则k<0
C.若x1+x2=0,则A、B关于原点对称
D.若k>0,x1>x2>0,则y2>y1>0
试题分析:根据反比例函数的性质判断即可.
答案详解:解:A.∵x1x2<0,
∴点A(x1,y1),B(x2,y2)(x1≠x2)在第一、三象限或第二、四象限,
∴y1y2<0,故A说法正确;
B.∵(x1﹣x2)(y1﹣y2)<0,
∴x1﹣x2>0,y1﹣y2<0或x1﹣x2<0,y1﹣y2>0,
∴x1>x2,则y1<y2或x1<x2,则y1>y2,
∴反比例函数y=kx的图象在第一、三象限,
∴k>0,故B说法错误;
C.∵x1+x2=0,
∴x1=﹣x2,
∴y1=k−x2=−y2,
∴y1+y2=0,
∴A、B关于原点对称,故C说法正确;
D.若k>0,则反比例函数y=kx的图象在第一、三象限,且在每个象限y随x的增大而减小,
∴当x1>x2>0时,y2>y1>0,故D说法正确;
所以选:B.
5.如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为( )
A.2B.22C.3D.10
试题分析:过点G作GH⊥BC,垂足为H,可得∠GHF=90°,根据正方形的性质可得AB=CD=4,∠B=90°,根据旋转的性质可得EF=FG,∠EFG=90°,然后利用同角的余角相等可得∠BEF=∠GFH,从而可证△EBF≌△FHG,进而可得BF=GH=1,最后可得点G在与BC平行且与BC的距离为1的直线上,从而可得当点G在CD边上时,DG的值最小,进行计算即可解答.
答案详解:解:过点G作GH⊥BC,垂足为H,
∴∠GHF=90°,
∵四边形ABCD是正方形,
∴AB=CD=4,∠B=90°,
∴∠B=∠GHF=90°,
由旋转得:
EF=FG,∠EFG=90°,
∴∠EFB+∠GFH=90°,
∵∠BEF+∠BFE=90°,
∴∠BEF=∠GFH,
∴△EBF≌△FHG(AAS),
∴BF=GH=1,
∴点G在与BC平行且与BC的距离为1的直线上,
∴当点G在CD边上时,DG最小且DG=4﹣1=3,
∴DG的最小值为3,
所以选:C.
6.如图,以Rt△ABC的斜边BC为边,在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.若AB=2,AO=32,则AC的长等于( )
A.122B.8C.4+32D.2+32
试题分析:根据图形的性质可将图形补全为外弦图,可得到点O是两个正方形的中心,再根据等腰直角三角形的性质可得结论;
答案详解:解:如图,过点F作FG⊥BA交BA的延长线于点G,过点E作EH⊥FG于点H,过点E作ED⊥AC于点D,连接OD,
则有AB=CD=2,且△OAD是等腰直角三角形,
∵AO=32,
∴AD=2OA=6,
∴AC=AD+CD=8.
所以选:B.
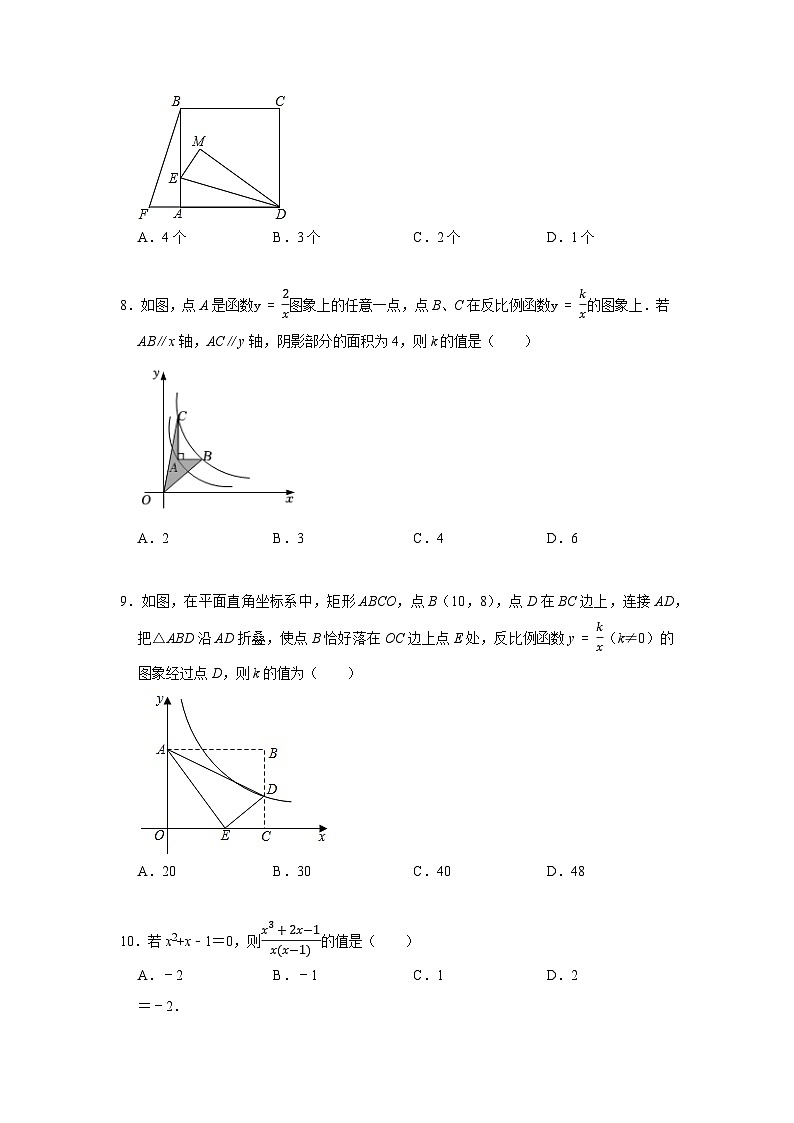
7.如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:
①若延长DE,则DE⊥BF; ②若连接AM,则AM∥FB; ③连接FE,当F、E、M三点共线时,AE=42−4;④连接EF、EC、FC,若△FEC是等腰三角形,则AE=43−4;其中正确有( )
A.4个B.3个C.2个D.1个
试题分析:①连接AM,延长DE交BF于J,由旋转的性质可得∠ABF=∠ADE,∠BAF=∠DAE=90°,由余角的性质可得∠BJE=90°,可得DJ⊥BF,故①正确;
②由折叠的性质可得DE⊥AM,可得AM∥BF,故②正确;
③当F、E、M共线时,易证∠DEA=∠DEM=67.5°,在MD上取一点J,使得ME=MJ,连接EJ,设AE=EM=MJ=x,则EJ=JD=2x,构建方程即可解决问题;
④连接EC,CF,只有EF=CE,设AE=AF=m,利用勾股定理构建方程即可解决问题.
答案详解:解:①如图1中,连接AM,延长DE交BF于J.
由旋转的性质得:△BAF≌△DAE,
∴∠ABF=∠ADE,∠BAF=∠DAE=90°,
∵∠ADE+∠AED=90°,∠AED=∠BEJ,
∴∠BEJ+∠EBJ=90°,
∴∠BJE=90°,
∴DJ⊥BF,故①正确;
②由翻折可知:EA=EM,DM=DA,∠AED=∠MED,
∴DE垂直平分线段AM,
∴DE⊥AM,
∴AM∥BF,故②正确,
③如图2中,当F、E、M共线时,
∵AE=AF,∠BAF=90°,
∴∠AEF=∠AFE=45°,
∴∠DEA=∠DEM=67.5°,
在MD上取一点J,使得ME=MJ,连接EJ,
∵∠MEJ=∠MJE=45°,
∴∠JED=∠JDE=12∠MJE=22.5°,
∴EJ=JD,
设AE=EM=MJ=x,则EJ=JD=2x,
则有x+2x=4,
∴x=42−4,
∴AE=42−4,故③正确,
③如图3中,连接EC,CF,
∵∠AEF=45°,∠AED=67.5°,
∴∠DEF=45°+67.5°=112.5°,
∴∠CEF>90°,
∵△FEC是等腰三角形,
∴EF=CE,
设AE=AF=m,
则有:2m2=42+(4﹣m)2,
∴m=43−4或﹣43−4(舍弃),
∴AE=43−4,故④正确;
所以选:A.
8.如图,点A是函数y=2x图象上的任意一点,点B、C在反比例函数y=kx的图象上.若AB∥x轴,AC∥y轴,阴影部分的面积为4,则k的值是( )
A.2B.3C.4D.6
试题分析:由反比例函数系数k的几何意义可得S阴影部分=S矩形ABMN=4,利用反比例函数图象上点的坐标特征,设点A的横坐标为a,用代数式表示MN、AM,列方程求解即可.
答案详解:解:如图,延长CA交x轴于点N,过点B作BM⊥x轴,垂足为M,
∵S阴影部分=S△CON+S矩形ABMN﹣S△BOM,而S△CON=S△BOM=12|k|,
∴S阴影部分=S矩形ABMN=4,
设ON=a,
∵点A在反比例函数y=2x的图象上,
∴AN=2a=BM,
又∵点B在反比例函数y=kx的图象上,
∴OM=ak2,
∴MN=ak2−a,
由S阴影部分=S矩形ABMN=4得,
(ak2−a)×2a=4,
即k﹣2=4,
∴k=6,
所以选:D.
9.如图,在平面直角坐标系中,矩形ABCO,点B(10,8),点D在BC边上,连接AD,把△ABD沿AD折叠,使点B恰好落在OC边上点E处,反比例函数y=kx(k≠0)的图象经过点D,则k的值为( )
A.20B.30C.40D.48
试题分析:根据翻折变换的性质,可得AE=AB=5,DE=BD;然后设点D的坐标是(10,b),在Rt△CDE中,根据勾股定理,求出CD的长度,进而求出k的值.
答案详解:解:∵△ABD沿AD折叠,使点B恰好落在OC边上点E处,点B(10,8),
∴AE=AB=10,DE=BD,
∵AO=8,AE=10,
∴OE=AE2−OA2=6,CE=10﹣6=4,
设点D的坐标是(10,b),
则CD=b,DE=8﹣b,
∵CD2+CE2=DE2,
∴b2+42=(8﹣b)2,
解得b=3,
∴点D的坐标是(10,3),
∵反比例函数的图象经过点D,
∴k=10×3=30,
所以选:B.
10.若x2+x﹣1=0,则x3+2x−1x(x−1)的值是( )
A.﹣2B.﹣1C.1D.2
试题分析:将x2+x﹣1=0变形得x2=1﹣x,代入所求式中,整体代入若干次,化简可得答案.
答案详解:解:∵x2+x﹣1=0,
∴x2=1﹣x,
∴x3+2x−1x(x−1)
=x(1−x)+2x−11−x−x
=3x−x2−11−2x
=3x−1−(1−x)1−2x
=4x−21−2x
=﹣2.
所以选:A.
11.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
A.AD=3B.AD=4C.AD=5D.AD=6
试题分析:先证四边形PMEN是平行四边形,当∠APB=90°时,四边形PMEN是矩形,设DP=x,CP=10﹣x,再由勾股定理得出方程,分别计算即可.
答案详解:解:方法1:∵四边形ABCD是矩形,
∴AD=BC,AB=CD=10,∠C=∠D=90°,
∵M、N、E分别是PA、PB、AB的中点,
∴ME、NE是△ABP的中位线,
∴ME∥BP,NE∥AP,
∴四边形PMEN是平行四边形,
当∠APB=90°时,四边形PMEN是矩形,
设DP=x,CP=10﹣x,
由勾股定理得:AP2=AD2+x2,BP2=BC2+(10﹣x)2,AP2+BP2=AB2,
∴AD2+x2+AD2+(10﹣x)2=102,
AD2+x2﹣10x=0,
①当AD=3时,x2﹣10x+9=0,
x=1或x=9,符合题意;
②当AD=4时,x2﹣10x+16=0,
x=2或x=8,符合题意;
③当AD=5时,x2﹣10x+25=0,
x=5,符合题意;
④当AD=6时,x2﹣10x+36=0,无解;
所以选:D.
方法2:
连接MN,PE,如图所示:
由方法1得:四边形PMEN是平行四边形,
∵M、N分别是PA、PB的中点,
∴MN是△PAB的中位线,
∴MN=12AB=5,
若四边形PMEN是矩形,则PE=MN=5,
而当AD=6时,PE不可能等于5,
∴当AD=6时,四边形PMEN不可能为矩形,
所以选:D.
12.若关于x的分式方程x−a3x−6+x+1x−2=1的解为非负数,且关于y的不等式组y+6≤2(y+2)3y−a3<1有3个整数解,则所有满足条件的整数a的值之和为( )
A.19B.22C.30D.33
试题分析:求出分式方程的解,根据解为非负数可得a的取值范围,再根据不等式组的整数解的个数确定a的取值范围,再根据a为整数进行计算即可.
答案详解:解:解关于x的分式方程x−a3x−6+x+1x−2=1得,
x=a﹣9,
由于方程的解为非负数,而x=2是增根,
∴a﹣9≥0且a﹣9≠2,
即a≥9且a≠11,
不等式①的解集为y≥2,
不等式②的解集为y<a+33,
由于2≤y<a+33的整数解只有3个,
∴4<a+33≤5,
解得9<a≤12,
又∵a为整数,且a≠11,
∴a=10,12,
∴所有满足条件的整数a的值之和为22,
所以选:B.
13.如图1,点P从菱形ABCD的顶点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,点P运动时△PAD的面积y(cm2)随时间x(s)变化的关系如图2,则a的值为( )
A.354B.253C.192D.9
试题分析:过点C作CE⊥AD,再根据图象的三角形的面积可得CE=8,再利用菱形的性质和勾股定理列方程可求a即可.
答案详解:解:过点C作CE⊥AD,
∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴点P在边BC上运动时,y的值不变,
∴AD=BC=10+a﹣10=a,
即菱形的边长是a,
∴12AD•CE=4a,即CE=8,
当点P在AC上运动时,y逐渐增大,
∴AC=10,
∴AE=AC2−CE2=102−82=6,
在Rt△DCE中,DC=a,DE=a﹣6,CE=8,
∴a2=82+(a﹣6)2,
解得:a=253.
所以选:B.
14.函数y=1x−2+3的图象可以由y=1x的图象先向右平移2个单位,再向上平移3个单位得到.根据所获信息判断,下列直线中与函数y=1x−1−2的图象没有公共点的是( )
A.经过点(0,2)且平行于x轴的直线
B.经过点(0,﹣3)且平行于x轴的直线
C.经过点(﹣1,0)且平行于y轴的直线
D.经过点(1,0)且平行于y轴的直线
试题分析:根据题意可以知道平移后的反比例函数不会与直线x=1、直线y=﹣2相交,判断出答案即可.
答案详解:解:根据题意可知,如下图所示,图1根据题意平移后得到图2,
函数y=1x−1−2的图象是函数y=1x的图象向右平移1个单位,在向下平移2个单位得到的,
∴由反比例函数的图象的性质和平移的定义可知,函数y=1x−1−2的图象与直线x=1、直线y=﹣2不会相交.
所以选:D.
15.如图,点F是菱形对角线BD上一动点,点E是线段BC上一点,且CE=4BE,连接EF、CF,设BF的长为x,EF+CF=y,点F从点B运动到点D时,y随x变化的关系图象,图象最低点的纵坐标是( )
A.35B.1255C.42D.532
试题分析:如图1,连接AF,由对称的性质可得AF=CF,所以y=EF+CF=EF+AF,当A、F、E三点在同一直线上时,y取最小值,y的最小值为线段AE的长,根据图2可计算BC=5,如图3,作辅助线,构建直角三角形,计算AE的长可解答.
答案详解:解:如图1,连接AF,AE,AE交BD于F1,
∵在菱形ABCD中点A,点C关于BD对称,
∴AF=CF,
∴y=EF+CF=EF+AF,
当A、F、E三点在同一直线上时,y取最小值,y的最小值为线段AE的长,
如图2,当x=0时,y=6,
设BE=a,则CE=4a,
∴y=a+5a=6,
∴a=1,
∴BC=5,
由图2知:BD=6,
如图3,连接AC交BD于G,连接EG,过点E作EH⊥AC于H,
∵四边形ABCD是菱形,
∴AC⊥BD,BG=12BD=3,
由勾股定理得:CG=4,
∴△ECG的面积=45S△BCG=12•CG•EH,
∴45×12×3×4=12×4×EH,
∴EH=125,
∴CH=CE2−EH2=42−(125)2=165,
∴AH=AC﹣CH=8−165=245,
∴AE=AH2+EH2=(245)2+(125)2=1255,
即图象最低点的纵坐标是1255.
所以选:B.
16.如图,在四边形ABCD中,∠ABC=90°,AB=BC=22,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,△BEF的面积是2.5,下列选项正确的是( )
①EF=2;
②S△ABE=S△BCF;
③四边形BEDF的面积是4;
④D到EF的距离为0.5.
A.①③B.①④C.②③D.②④
试题分析:连接AC、BD,根据勾股定理求出AC,根据三角形中位线定理求出EF;根据三角形的面积公式判断SABE与S△BCF的关系;根据三角形中位线定理、三角形的面积公式求出四边形BEDF的面积;根据三角形的面积公式求出D到EF的距离,判断即可.
答案详解:解:连接AC、BD,
在Rt△ABC中,∠ABC=90°,AB=BC=22,
则AC=AB2+BC2=4,
∵E、F分别是AD、CD的中点,
∴EF是△DAC的中位线,
∴EF=12AC=2,①正确;
∵E、F分别是AD、CD的中点,
∴SABE=12S△ABD,S△BCF=12S△BCD,
∵S△ABD与S△BCD的大小不确定,
∴SABE与S△BCF不一定相等,②错误;
∵S△ABC=12×22×22=4,S四边形ABCD=6,
∴S△ADC=2,
∵E、F分别是AD、CD的中点,
∴S△DEF=12,
∵S△BEF=2.5,
∴S四边形BEDF=3,③错误;
∵S△DEF=12,EF=2,
∴D到EF的距离为0.5,④正确;
所以选:B.
17.已知△ABC中,AB=1,BC=4,以AC为边长作等边三角形ACD,连接BD,则BD的长不可能为( )
A.3B.4C.5D.6
试题分析:以AB为边作等边△ABE,根据题意得到△DAB≌△CAE (SAS),根据全等三角形的性质得出BD=CE,据此即可得解.
答案详解:解:如图,以AB为边作等边△ABE,
∵△ACD,△ABE是等边三角形,
∴AD=AC,AB=AE=BE=1,∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,
即∠EAC=∠BAD,
在△DAB和△CAE中,
AB=AE∠BAD=∠EACAD=AC,
∴△DAB≌△CAE (SAS),
∴BD=CE,
若点E,点B,点C不共线时,EC<BC+BE;若点E,点B,点C共线时,EC=BC+BE,
∴EC≤BC+BE=5,
∴EC的最大值为5,
即BD的最大值为5,BD的长不可能为6,
所以选:D.
18.如图,矩形ABCD的边CD上有一点E,DE=1,∠DAE=22.5°,EF⊥AB,垂足为F,将△AEF绕着点F顺时针旋转,使得点A的对应点G落在EF上,点E恰好落在点B处,连接BE.有下列结论:
①AB=BE;
②BG平分∠EBF;
③△BFG的面积是四边形EFBC面积的14;
④BE=2+2.
其中结论正确的是( )
A.①②③B.②③④C.①②④D.①③④
试题分析:由角的数量关系可求∠AEB=67.5°=∠EAF,可得AB=BE,故①正确;计算出∠EBG=22.5°,得出∠EBG=∠FBG,故②正确;过点G作GM⊥BE于点M,由角平分线的性质可得GF=GM,根据直角三角形的斜边大于直角边得出GE>GM=GF,从而根据三角形的面积公式得出结论,得到③错误;连接AG,根据等腰直角三角形的性质可知AG=2,推导得出AG=EG=2,从而EF=EG+FG=2+1,再由BE=BF+AF,判断出④正确.
答案详解:解:由旋转的性质可得:EF=FB,∠EFB=90°,
∵四边形ABCD是矩形,EF⊥AB,
∴∠ABC=∠C=∠EFB=90°,
∴四边形EFBC是矩形,
又∵EF=BF,
∴矩形EFBC是正方形,
∴∠BEF=∠EBF=45°,
∵∠DAE=∠AEF=22.5°,
∴∠AEB=∠FEB+∠AEF=67.5°=90°﹣22.5°=∠EAF,
∴AB=BE,
故①正确;
∵∠EBF=45°,∠FBG=∠AEF=∠DAE=22.5°,
∴∠EBG=45°﹣22.5°=22.5°,
∴∠EBG=∠FBG,
∴BG平分∠EBF,
故②正确;
过点G作GM⊥BE于点M,如图1,
∵BG平分∠EBF,
∴GF=GM,
在Rt△GME中,GE>GM=GF,
∴S△BFG≠12S△BFE,
∵S△BFE=12S四边形EFBC,
∴S△BFG≠14S四边形的EFBC,
故③错误;
连接AG,如图1,
∵∠AFG=90°,DE=AF=FG=1,
∴∠GAF=45°,AG=2,
∴∠EAG=67.5°﹣45°=22.5°,
∴∠AEG=∠GAE,
∴EG=AG=2,
∴EF=EG+FG=2+1,
又∵EF=BF,AB=BE,
∴BE=BF+AF=2+1+1=2+2,
故④正确,
∴正确的是:①②④,
所以选:C.
19.如图,将平行四边形ABCD绕点A逆时针旋转到平行四边形A′B′C′D′的位置,使点B'落在BC上,B′C′与CD交于点E,若AB=3,BC=4,BB′=1,则CE的长为( )
A.98B.76C.87D.1
试题分析:由相似三角形的性质可求DD'的长,通过证明△CEB′∽△C'ED,可求解.
答案详解:解:如图,连接DD',
由旋转可知,∠BAB′=∠DAD′,AB′=AB=3,AD′=AD=4,
∴△BAB′∽△DAD′,
∴AB:BB′=AD:DD′=3:1,∠AD′D=∠AB′B=∠B,
∴DD′=43,
又∵∠AD′C′=∠AB′C′=∠B,∠AD′D=∠B=∠AB′B,
∴∠AD′C′=∠AD′D,即点D′,D,C′在同一条直线上,
∴DC′=53,
又∠C′=∠ECB′,∠DEC′=∠B′EC,
∴△CEB′∽△C'ED,
∴B′E:DE=CE:C′E=B′C:DC′,即B′E:DE=CE:C′E=3:53,
设CE=x,B'E=y,
∴x:(4﹣y)=y:(3﹣x)=3:53,
∴x=98,
∴CE=98,
所以选:A.
20.如图,在Rt△ABC中,∠CAB=90°,AB=8,AC=3,两顶点A、B分别在平面直角坐标系的y轴、x轴的正半轴上滑动,点C在第一象限内,连接OC,则OC的长的最大值为( )
A.8B.9C.4+22D.4+32
试题分析:取AB中点P,连接OP、CP,根据直角三角形的性质求出OP,根据勾股定理求出PC,根据三角形的三边关系解答即可.
答案详解:解:取AB中点P,连接OP、CP,
则OP=AP=12AB=4,
由勾股定理得,CP=AC2+AP2=5,
利用三角形两边之和大于点三边可知:OC≤OP+PC=9,OC的长的最大值为9,
所以选:B.
21.如图,在直角坐标系中,点A在函数y=kx(x>0)的图象上,AB⊥x轴于点B,AB的垂直平分线与y轴交于点C,与函数y=kx(x>0)的图象交于点D,连结AC,CB,BD,DA,若四边形ACBD的面积等于23,则k的值为( )
A.4 3B.23C.4D.3
试题分析:设A(a,ka),可求出D(2a,k2a),由于对角线垂直,所以面积=对角线乘积的一半即可.
答案详解:解:设A(a,ka),可求出D(2a,k2a),
∵AB⊥CD,
∴S四边形ACBD=12AB•CD=12×2a×ka=23,
解得k=23.
所以选:B.
22.如图,在矩形ABCD中,AB=6,BC=8.点O为矩形ABCD的对称中心,点E为边AB上的动点,连接EO并延长交CD于点F.将四边形AEFD沿着EF翻折,得到四边形A′EFD′,边A′E交边BC于点G,连接OG、OC,则△OGC的面积的最小值为( )
A.18﹣37B.92+37C.12−372D.6+372
试题分析:在EA上截取EM=EG,连接OM,证明△MOE≌△GOE,所以OM=OG,即可得OM最短时,OG也就最短,而当OM⊥AB时,OM最短,且OM=4=OG,再过点O作OH⊥BC,得OH=3,又因为OC=5,就可以根据勾股定理计算GH、HC的长,从而计算出最小面积.
答案详解:解:在EA上截取EM=EG,连接OM,
由折叠得:∠MEO=∠GEO,
又∵EO=EO,
∴△MOE≌△GOE,
∴OM=OG,
∴OM最短时,OG也就最短,
而当OM⊥AB时,OM最短,
此时,∵点O为矩形ABCD的对称中心,
∴OM=12BC=4=OG,
即OG的最小值是4,
在△OGC中,∵点O为矩形ABCD的对称中心,
∴OC长度是矩形对角线长度的一半,即是5,定值,∠BCO度数也不变,是定值,
∴当OG=4最小值时,△OGC面积最小.
过点O作OH⊥BC,
∵点O为矩形ABCD的对称中心,
∴OH=12AB=3,
∴Rt△OGH中,GH=OG2−OH2=42−32=7,
Rt△OHC中,HC=OC2−OH2=52−32=4,
∴GC=GH+HC=7+4,
∴△OGC面积的最小值是12×GC×OH=12×(7+4)×3=327+6.
所以选:D.
23.点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )
A.75°B.60°C.45°D.30°
试题分析:过E作AB的延长线AF的垂线,垂足为F,可得出∠F为直角,又四边形ABCD为正方形,可得出∠A为直角,进而得到一对角相等,由旋转可得∠DPE为直角,根据平角的定义得到一对角互余,在直角三角形ADP中,根据两锐角互余得到一对角互余,根据等角的余角相等可得出一对角相等,再由PD=PE,利用AAS可得出三角形ADP与三角形PEF全等,根据确定三角形的对应边相等可得出AD=PF,AP=EF,再由正方形的边长相等得到AD=AB,由AP+PB=PB+BF,得到AP=BF,等量代换可得出EF=BF,即三角形BEF为等腰直角三角形,可得出∠EBF为45°,再由∠CBF为直角,即可求出∠CBE的度数.
答案详解:解:过点E作EF⊥AF,交AB的延长线于点F,则∠F=90°,
∵四边形ABCD为正方形,
∴AD=AB,∠A=∠ABC=90°,
∴∠ADP+∠APD=90°,
由旋转可得:PD=PE,∠DPE=90°,
∴∠APD+∠EPF=90°,
∴∠ADP=∠EPF,
在△APD和△FEP中,
∵∠ADP=∠FPE∠A=∠F=90°PD=EP,
∴△APD≌△FEP(AAS),
∴AP=EF,AD=PF,
又∵AD=AB,
∴PF=AB,即AP+PB=PB+BF,
∴AP=BF,
∴BF=EF,又∠F=90°,
∴△BEF为等腰直角三角形,
∴∠EBF=45°,又∠CBF=90°,
则∠CBE=45°.
所以选:C.
24.如图,以矩形OABC的顶点O为坐标原点建立平面直角坐标系,使点A、C分别在x轴、y轴的正半轴上,双曲线y=kx(x>0)的图象经过BC的中点D,且与AB交于点E.过OC边上一点F,把△BCF沿直线BF翻折,使点C落在点C′处(点C′在矩形OABC内部),且C′E∥BC,若点C′的坐标为(2,3),则k的值为( )
A.274B.272C.392D.394
试题分析:首先证明点E是线段AB的中点,设BC=BC′=m,则EC′=m﹣2.在Rt△BEC′中,根据BC′2=BE2+EC′2,构建方程求出m即可解决问题;
答案详解:解:连接OD、OE.设BC=BC′=m,则EC′=m﹣2.
∵CD=BD,
∴S△CDO=k2=14S矩形ABCD,
∵S△AOE=k2=S△CDO=14S矩形ABCD,
∴AE=EB,
∵C′(2,3),
∴AE=EB=3,
在Rt△BEC′中,∵BC′2=BE2+EC′2,
∴m2=32+(m﹣2)2,
∴m=134,
∴E(134,3),
∵点E在y=kx上,
∴k=394,
所以选:D.
25.如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线y=6x(x>0)上,连接BC交AD于P,连接OP,则图中S△OBP是( )
A.6B.3C.6D.12
试题分析:先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°,故可得出AD∥OB,所以S△ABP=S△AOP,故S△OBP=S△AOB,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
答案详解:解:如图:
∵△AOB和△ACD均为正三角形,
∴∠AOB=∠CAD=60°,
∴AD∥OB,
∴S△ABP=S△AOP,
∴S△OBP=S△AOB,
过点B作BE⊥OA于点E,则S△OBE=S△ABE=12S△AOB,
∵点B在反比例函数y=6x的图象上,
∴S△OBE=12×6=3,
∴S△OBP=S△AOB=2S△OBE=6.
所以选:C.
26.如图,正方形ABCD的边长为4,∠BCM=30°,点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( )
A.42−4B.22−2C.26−23D.26−3
试题分析:如图,连接BD,在BD上截取BG,使得BG=BC,连接FG,过点D作DH⊥GF于点H.证明△CBE≌△GBF(SAS),推出∠BCE=∠BGF=30°,推出点F在直线GF上运动,当点F与H重合时,DF的值最小,作出DH即可解决问题.
答案详解:解:如图,连接BD,在BD上截取BG,使得BG=BC,连接FG,过点D作DH⊥GF于点H.
∵四边形ABCD是正方形,
∴∠CBD=45°,CD=CB=4,∠DCB=90°,
∴BD=42,BG=BC=4,
∴DG=BD﹣BG=42−4,
∵∠CBG=∠EBF=45°,
∴∠CBE=∠GBF,
在△CBE和△GBF中,
CB=GB∠CBE=∠GBFBE=BF,
∴△CBE≌△GBF(SAS),
∴∠BCE=∠BGF=30°,
∴点F在直线GF上运动,当点F与H重合时,DF的值最小,
∵DH⊥FH,∠DGH=∠BGF=30°
∴DH=12DG=22−2,
∴DF的最小值为22−2,
所以选:B.
27.如图,在给定的正方形ABCD中,点E从点B出发,沿边BC方向向终点C运动,DF⊥AE交AB于点F,以FD,FE为邻边构造平行四边形DFEP,连接CP,则∠DFE+∠EPC的度数的变化情况是( )
A.一直减小B.一直减小后增大
C.一直不变D.先增大后减小
试题分析:根据题意∠DFE+∠EPC=∠DPC,作PH⊥BC交BC的延长线于H,证明CP是∠DCH的角平分线即可解决问题.
答案详解:解:作PH⊥BC交BC的延长线于H,
∵四边形ABCD是正方形,
∴AD=AB=BC,
∠DAF=∠ABE=∠DCB=∠DCH=90°,
∵DF⊥AE,
∴∠BAE+∠DAE=90°,∠ADF+∠DAE=90°,
∴∠BAE=∠ADF,
∴△ADF≌△BAE(ASA),
∴DF=AE,
∵四边形DFEP是平行四边形,
∴DF=PE,∠DFE=∠DPE,
∵∠BAE+∠AEB=90°,∠AEB+∠PEH=90°,
∴∠BAE=∠PEH,
∵∠ABE=∠H=90°,AE=EP.
∴△ABE≌△EHP(AAS),
∴PH=BE,AB=EH=BC,
∴BE=CH=PH,
∴∠PCH=45°,
∵∠DCH=90°,
∴∠DCP=∠PCH,
∴CP是∠DCH的角平分线,
∴点P的运动轨迹是∠DCH的角平分线,
∵∠DFE+∠EPC=∠DPE+∠EPC=∠DPC,
观察图象可得,∠DPC一直减小,
所以选:A.
28.如图,在平行四边形ABCD中,对角线相交于点O,AC=AB,E是AB边的中点,G、F为BC上的点,连接OG和EF,若AB=13,BC=10,GF=5,则图中阴影部分的面积为( )
A.48B.36C.30D.24
试题分析:连接EO,EG,OF,依据EO是△ABC的中位线,即可得出EO∥BC,EO=12BC=5,进而得到四边形EOFG是平行四边形,据此可得S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO,求得△ABO的面积即可得出结论.
答案详解:解:如图所示,连接EO,EG,OF,
∵平行四边形ABCD中,对角线相交于点O,
∴O是AC的中点,
又∵E是AB边的中点,
∴EO是△ABC的中位线,
∴EO∥BC,EO=12BC=5,
又∵GF=5,
∴EO=GF,
∴四边形EOFG是平行四边形,
∴S△EOP+S△FGP=12S四边形EOFG=S△EOG,
又∵EO∥BG,
∴S△EOG=S△EOB,
∴S△EOP+S△FGP=S△EOB,
∴S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO,
∵AC=AB=13,BC=10,
∴等腰△ABC中BC边上的高为132−52=12,
∴S△ABC=12×10×12=60,
∵O是AC的中点,
∴S△ABO=12S△ABC=12×60=30,
∴阴影部分的面积为30,
所以选:C.
29.如图,在正方形ABCD中,AB=4,点P在对角线BD上,PE⊥BC,PF⊥CD,垂足分别为E,F,连结AP、EF,以下结论中:①AP=EF;②AP⊥EF;③EF的最小值为2.其中正确的是( )
A.①②B.②③C.①③D.①②③
试题分析:①证明△ADP≌△CDP,则AP=PC,根据矩形对角线相等得PC=EF,即可判断;
②证明△AGP≌△FPE(SAS),得到∠BAP=∠PFE,进而求解;
③当AP⊥BD时,即AP=12BD=22时,EF的最小值等于22,即可判断.
答案详解:解:①连接PC,EF,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∵PE⊥BC,PF⊥CD,
∴四边形PECF为矩形,
∴PC=EF,
∵四边形ABCD为正方形,
∴AD=CD,∠ADC=∠CDP,
在△ADP和△CDP中,
AD=CD∠ADP=∠CDPDP=DP,
∴△ADP≌△CDP(SAS),
∴AP=PC,
∴AP=EF;
故①正确;
②延长FP与AB交于点M,延长AP与EF交于点H,
∵BD平分∠ABC,PM⊥AB,PE⊥BC,
∴PM=PE,
∵AP=EF,∠AMP=∠EPF=90°,
∴△AMP≌△FPE(HL),
∴∠BAP=∠PFE,
∵∠AMP=90°,
∴∠BAP+∠APM=90°,
∵∠APM=∠HPF,
∴∠PFH+∠HPF=90°,
∴AP⊥EF,
故②正确;
③由EF=PC=AP,
∴当AP最小时,EF最小,
则当AP⊥BD时,即AP=12BD=22时,EF的最小值等于22;
故③不正确;
综上,①②正确.
所以选:A.
30.平面直角坐标系中,菱形ABCD如图所示,OA=3,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒45°,则第2022秒时点D的对应坐标为( )
A.(23,3)B.(﹣23,﹣3)C.(3,﹣23)D.(﹣3,23)
试题分析:根据菱形的性质和垂直平分线的性质,可以得到点D的坐标,然后根据旋转的性质,可以得到点D在第2022秒对应的点D在第四象限,然后即可写出点D对应的坐标.
答案详解:解:作DE⊥BC于点E,如右图所示,
由题意可得,BE=EC=OB,
∵OA=3,∠AOB=90°,AB=2OB,
∴OB=3,AB=23,
∴点D的坐标为(23,3),
∵360°÷45°=8,2022÷8=252…6,
∴第2022秒时点D的对应坐标为在第四象限,此时点D对应的坐标为(3,﹣23),
所以选:C.
31.关于x的方程(x﹣2)(x+1)=p2(p为常数)根的情况,下列结论中正确的是( )
A.有两个相异正根B.有两个相异负根
C.有一个正根和一个负根D.无实数根
试题分析:先计算根的判别式的值得到Δ>0,则可判断方程有两个不相等的实数解,设方程的两个分别为x1,x2,利用根与系数的关系得x1+x2=1>0,x1x2=﹣2﹣p2<0,根据有理数的性质得到x1、x2的符合相反,且正根的绝对值较大,于是可对各选项进行判断.
答案详解:解:方程化为一般式为x2﹣x﹣2﹣p2=0,
∵Δ=(﹣1)2﹣4(﹣2﹣p2)=4p2+9>0,
∴方程有两个不相等的实数解,
设方程的两个分别为x1,x2,
根据根与系数的关系得x1+x2=1>0,x1x2=﹣2﹣p2<0,
∴方程有一个正根和一个负根.
所以选:C.
32.如图,在正方形ABCD中,AB=8,若点E在对角线AC上运动,将线段DE绕点D逆时针旋转90°得到线段DF,连接EF、CF.点P在CD上,且CP=3PD.给出以下几个结论①EF=2DE,②EF2=AE2+CE2,③线段PF的最小值是42,④△CFE的面积最大是16.其中正确的是( )
A.①②④B.②③④C.①②③D.①③④
试题分析:①根据旋转的性质得△DEF为等腰直角三角形,进而得到EF与DE的数量关系,便可判定①的正误;
②证明△ADE≌△CDF,得AE=CF,∠DAE=∠DCF=45°,再在直角△CEF中由勾股定理得EF2=CF2+CE2,进而得EF2=AE2+CE2,便可判断②的正误;
③由∠DCF=45°恒成立,所以当PF⊥CF时,PF取最小值,求出此时的PF便可判断③的正误;
④先求得AE+CE=AC=2AD=82,再根据((AE﹣CE)2≥0求得AE•CE≤32,求得AE•CE的最大值为32,进而求得△CFE的面积最大值,便可判断④的正误.
答案详解:解:①∵由旋转知,DE=DF,∠EDF=90°,
∴EF=2DE,
故①正确;
②∵四边形ABCD是正方形,
∴∠ADC=∠BCD=90°,AD=CD,∠DAC=∠ACD=45°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(SAS),
∴AE=CF,∠DAE=∠DCF=45°,
∴∠ECF=90°,
∴EF2=CF2+CE2,
∴EF2=AE2+CE2,
故②正确;
③∵CP=3PD.
∴PC=34CD=6,
当PF⊥CF时,PF取最小值,如图,
∵∠DCF=45°,
∴PF=CF=22CP=32,
故③错误;
④∵∠ECF=90°,
∴S△CEF=12CE⋅CF=12CE⋅AE,
∵AE+CE=AC=2AD=82,
∴(AE﹣CE)2=(AE+CE)2﹣4AE•CE=128﹣4AE•CE≥0,
∴AE•CE≤32,
∴AE•CE的最大值为32,
∴△CFE的面积最大是12×32=16,
故④正确;
所以选:A.
33.如图,边长为1的正方形ABCD绕点A逆时针旋转60°得到正方形AEFG,连接CF,则CF的长是( )
A.1B.2C.3D.32−3
试题分析:连接AC、AF,证明△ACF为等边三角形,求得AC便可得出结果.
答案详解:解:连接AC、AF,
由旋转性质得,AC=AF,∠CAF=60°,
∴△ACF为等边三角形,
∴AC=CF,
∵AC=2AB=2,
∴CF=2,
所以选:B.
34.若a1=x+1(x≠0且x≠﹣1),a2=11−a1,a3=11−a2,…,an=11−an−1,则a2022等于( )
A.xB.x+1C.−1xD.xx+1
试题分析:分别求出a2=−1x,a3=xx+1,a4=x+1,a5=−1x,根据求出的结果得出每三个数就循环一次,再根据得出的规律得出答案即可.
答案详解:解:∵a1=x+1,
∴a2=11−a1=11−(x+1)=−1x,
∴a3=11−a2=11−(−1x)=xx+1,
∴a4=11−a3=11−xx+1=x+1,
∴该数列每三个数就循环一次,
∵2022÷3=674,
∴a2022=xx+1,
所以选:D.
35.如图,把正方形纸片ABCD沿对边中点所在直线折叠后展开,折痕为MN;再过点D折叠,使得点A落在MN上的点F处,折痕为DE,则EMFN的值是( )
A.3B.3−1C.2−3D.3−3
试题分析:设正方形纸片ABCD的边长为2a,由折叠的性质与正方形的性质可得AM=BM=DN=NC=a,AD=DF=MN=2a,AE=EF,∠EMF=∠DNF=90°,由勾股定理可求FN的长,进而可求FM的长,设AE=EF=x,再利用勾股定理可求x,得到EM的长,代入EMFN,计算即可.
答案详解:解:设正方形纸片ABCD的边长为2a.
由题意可知:AM=BM=DN=NC=a,AD=DF=MN=2a,AE=EF,∠EMF=∠DNF=90°,
∴FN=DF2−DN2=(2a)2−a2=3a,
∴FM=MN﹣FN=(2−3)a.
设AE=EF=x,则EM=AM﹣AE=a﹣x.
在Rt△EMF中,∵EM2+MF2=EF2,
∴(a﹣x)2+[(2−3)a]2=x2,
∴x=(4﹣23)a,
∴EM=a﹣(4﹣23)a=(23−3)a,
∴EMFN=(23−3)a3a=2−3.
所以选:C.
36.疫情期间,某校工作人员对教室进行消毒时,室内每立方米空气中的含药量y(毫升)与喷洒消毒液的时间x(分钟)成正比例关系,喷洒完成后,y与x成反比例关系(如图所示).已知喷洒消毒液用时6分钟,此时室内每立方米空气中的含药量为16毫升.问室内每立方米空气中的含药量不低于8毫升的持续时间为( )
A.7分钟B.8分钟C.9分钟D.10分钟
试题分析:分0≤x≤6和x>6两种情况,利用待定系数法分别求出对应的一次函数和反比例函数解析式,在两个函数解析式中求出y=8时,x的值,从而得到有效消毒时间.
答案详解:解:当0≤x≤6时,设y=mx,
将点(6,16)代入,得:16=6m,
解得m=83,
∴y=83x;
当x>6时,设y=nx,
将点(6,16)代入,得:16=n6,
解得:n=96,
∴y=96x;
综上,y=83x(0≤x≤6)96x(x>6);
当0≤x≤6时,若y=8,则83x=8,
解得x=3;
当x>6时,若y=8,则96x=8,
解得x=12;
∴12﹣3=9(分钟),
故室内每立方米空气中的含药量不低于8毫升的持续时间为9分钟.
所以选:C.
专题13 作图精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题13 作图精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题13作图精选原卷版docx、专题13作图精选解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
专题11 填空压轴题精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题11 填空压轴题精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题11填空压轴题精选原卷版docx、专题11填空压轴题精选解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
专题10 压轴大题精选(综合)-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题10 压轴大题精选(综合)-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题10压轴大题精选综合原卷版docx、专题10压轴大题精选综合解析版docx等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。












