专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版）

这是一份专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版），文件包含专题04易错题精选04之最值专题原卷版docx、专题04易错题精选04之最值专题解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

1．已知等边△ABC的边长为4，点P是边BC上的动点，将△ABP绕点A逆时针旋转60°得到△ACQ，点D是AC边的中点，连接DQ，则DQ的最小值是（ ）
A．2B．3C．2D．不能确定
试题分析：依据旋转的性质，即可得到∠BCQ＝120°，当DQ⊥CQ时，DQ的长最小，再根据勾股定理，即可得到DQ的最小值．
答案详解：解：如图，由旋转可得∠ACQ＝∠B＝60°，
又∵∠ACB＝60°，
∴∠BCQ＝120°，
∵点D是AC边的中点，
∴CD＝2，
当DQ⊥CQ时，DQ的长最小，
此时，∠CDQ＝30°，
∴CQ=12CD＝1，
∴DQ=22−12=3，
∴DQ的最小值是3，
所以选：B．
2．如图，E为正方形ABCD中BC边上的一点，且AB＝3BE＝3，M、N分别为边CD、AB上的动点，且始终保持MN⊥AE，则AM+NE的最小值为（ ）
A．4B．6C．25D．10
试题分析：由勾股定理可求AE的长，由“ASA”可证△ABE≌△DAH，可得DH=AE=10，通过证明四边形NEGM是平行四边形，可得NE=MG，MN=EG=AE=10，由AM+NE＝AM+MG，可得当点A，点M，点G三点共线时，AM+NE的最小值为AG，由勾股定理即可求解．
答案详解：解：过点D作DH∥MN，交AB于点H，过点E作EG∥MN，过点M作MG∥NE，两直线交于点G，连接AG，如图，
∵四边形ABCD是正方形，
∴AB∥CD，∠B＝∠BAD＝90°，
∵AB＝3BE＝3，
∴BE＝1，
∴AE=AB2+BE2=1+9=10，
∵DH∥MN，AB∥CD，
∴四边形DHNM是平行四边形，
∴DH＝MN，
∵MN⊥AE，DH∥MN，EG∥MN，
∴DH⊥AE，AE⊥EG，
∴∠BAE+∠AHD＝90°＝∠AHD+∠ADH，∠AEG＝90°，
∴∠BAE＝∠ADH，
在△ABE和△DAH中，∠BAE=∠ADHAB=AD∠B=∠BAD
∴△ABE≌△DAH（ASA），
∴DH=AE=10，
∴MN=DH=AE=10，
∵EG∥MN，MG∥NE，
∴四边形NEGM是平行四边形，
∴NE=MG，MN=EG=AE=10，
∴AM+NE＝AM+MG，
∴当点A，点M，点G三点共线时，AM+NE的最小值为AG，
∴AG=EG2+AE2=10+10=25．
所以选：C．
3．如图，在四边形ABCD中，点P是边CD上的动点，点Q是边BC上的定点，连接AP，PQ，E，F分别是AP，PQ的中点，连接EF．点P在由C到D运动过程中，线段EF的长度（ ）
A．保持不变B．逐渐变小
C．先变大，再变小D．逐渐变大
试题分析：连接AQ，根据三角形中位线定理解答即可．
答案详解：解：连接AQ，
∵点Q是边BC上的定点，
∴AQ的大小不变，
∵E，F分别是AP，PQ的中点，
∴EF=12AQ，
∴线段EF的长度保持不变，
所以选：A．
4．如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）
A．54B．1C．2D．52
试题分析：取CB的中点G，连接MG，根据等边三角形的性质可得BH＝BG，再求出∠HBN＝∠MBG，根据旋转的性质可得MB＝NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN＝MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH＝30°求解即可．
答案详解：解：如图，取BC的中点G，连接MG，
∵旋转角为60°，
∴∠MBH+∠HBN＝60°，
又∵∠MBH+∠MBC＝∠ABC＝60°，
∴∠HBN＝∠GBM，
∵CH是等边△ABC的对称轴，
∴HB=12AB，
∴HB＝BG，
又∵MB旋转到BN，
∴BM＝BN，
在△MBG和△NBH中，
BG=BH∠MBG=∠NBHMB=NB，
∴△MBG≌△NBH（SAS），
∴MG＝NH，
根据垂线段最短，MG⊥CH时，MG最短，即HN最短，
此时∵∠BCH=12×60°＝30°，CG=12AB=12×5=52，
∴MG=12CG=54，
∴HN=54，
所以选：A．
5．如图，在矩形ABCD中，AB＝2，AD＝5，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为（ ）
A．41B．29C．21D．212
试题分析：连接BP，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝2，连接PE、CE，则PC+QD＝PC+PB＝PC+PE≥CE，再根据勾股定理求解即可．
答案详解：解：如图，连接BP，
在矩形ABCD中，AD∥BC，AD＝BC＝5，
∵AP＝CQ，
∴AD﹣AP＝BC﹣CQ，
∴DP＝QB，DP∥BQ，
∴四边形DPBQ是平行四边形，
∴PB∥DQ，PB＝DQ，
则PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，
在BA的延长线上截取AE＝AB＝2，连接PE，
则BE＝2AB＝4，
∵PA⊥BE，
∴PA是BE的垂直平分线，
∴PB＝PE，
∴PC+PB＝PC+PE，
连接CE，则PC+QD＝PC+PB＝PC+PE≥CE，
∴CE=BE2+BC2=42+52=41，
∴PC+PB的最小值为41，
即PC+QD的最小值为41，
所以选A．
6．如图，在矩形ABCD中，AB＝12，AD＝7，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为（ ）
A．25B．24C．193D．13
试题分析：连接BP，在BA的延长线上截取AE＝AB＝12，连接PE，CE，PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，在BA的延长线上截取AE＝AB＝7，则PC+QD＝PC+PB＝PC+PE≥CE，根据勾股定理可得结果．
答案详解：解：如图，连接BP，
在矩形ABCD中，AD∥BC，AD＝BC，
∵AP＝CQ，
∴AD﹣AP＝BC﹣CQ，
∴DP＝QB，DP∥BQ，
∴四边形DPBQ是平行四边形，
∴PB∥DQ，PB＝DQ，
则PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，
在BA的延长线上截取AE＝AB＝12，连接PE，
∵PA⊥BE，
∴PA是BE的垂直平分线，
∴PB＝PE，
∴PC+PB＝PC+PE，
连接CE，则PC+QD＝PC+PB＝PC+PE≥CE，
∵BE＝2AB＝24，BC＝AD＝7，
∴CE=BE2+BC2=242+72=25．
∴PC+PB的最小值为25．
所以选：A．
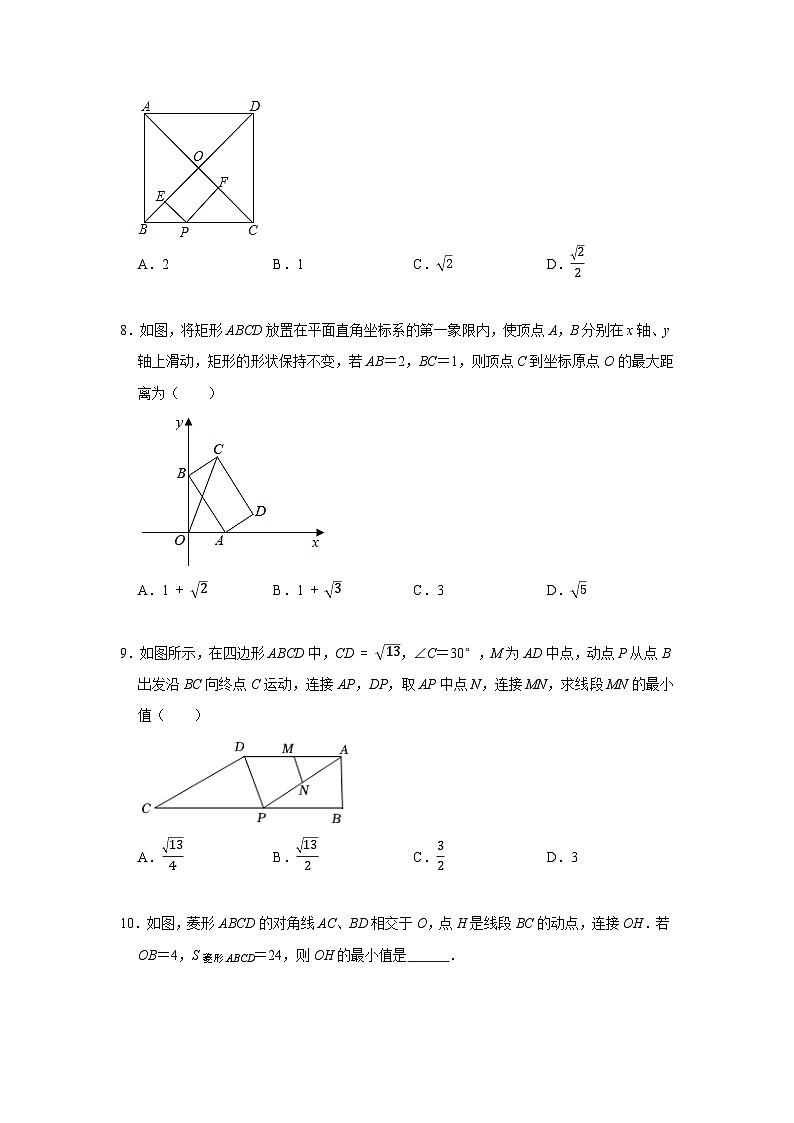
7．如图，正方形ABCD的对角线AC，BD相交于点O，点P是BC上任意一点，PE⊥BD于点E，PF⊥AC于点F，若AC＝22，则EF的长的最小值为（ ）
A．2B．1C．2D．22
试题分析：如图，连接OP、EF，根据已知条件和正方形的性质可以得到当EF最小就是OP最小，然后利用垂线段最短即可求解．
答案详解：解：如图，连接OP、EF，
∵正方形ABCD的对角线AC，BD相交于点O，点P是BC上任意一点，PE⊥BD于点E，PF⊥AC于点F，
∴四边形OEPF为矩形，
∴EF＝OP，
∴EF最小时OP最小，
当OP⊥BC于P的时候OP最小，
而当OP⊥BC时，P为BC的中点，
∴OP=12BC，
∵AC＝22，
则BC＝2，
∴OP＝1，
∴EF的长的最小值为1．
所以选：B．
8．如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB＝2，BC＝1，则顶点C到坐标原点O的最大距离为（ ）
A．1+2B．1+3C．3D．5
试题分析：取AD的中点E，连接OE，CE，OC，求得CE=2，OE＝1，再根据OC≤CE+OE＝1+2，即可得到点C到原点O距离的最大值是1+2．
答案详解：解：如图，取AB的中点E，连接OE，CE，OC，
∵∠AOB＝90°，
∴Rt△AOB中，OE=12AB＝1，
又∵∠ABC＝90°，AE＝BE＝CB＝1，
∴Rt△CBE中，CE=12+12=2，
又∵OC≤CE+OE＝1+2，
∴OC的最大值为1+2，
即点C到原点O距离的最大值是1+2，
所以选：A．
9．如图所示，在四边形ABCD中，CD=13，∠C＝30°，M为AD中点，动点P从点B出发沿BC向终点C运动，连接AP，DP，取AP中点N，连接MN，求线段MN的最小值（ ）
A．134B．132C．32D．3
试题分析：过点D作DE⊥BC于E，根据垂线段最短得到点P与点E重合时，DP最小，根据含30°角的直角三角形的性质求出DE，根据三角形中位线定理计算，得到答案．
答案详解：解：过点D作DE⊥BC于E，
则当点P与点E重合时，DP最小，
在Rt△CDE中，∠C＝30°，CD=13，
则DE=12CD=132，
∵M为AD中点，N是AP中点，
∴MN=12DP，
∴线段MN的最小值为134，
所以选：A．
10．如图，菱形ABCD的对角线AC、BD相交于O，点H是线段BC的动点，连接OH．若OB＝4，S菱形ABCD＝24，则OH的最小值是 2.4 ．
试题分析：根据菱形面积等于对角线乘积的一半求出AC，再由动点H运动特点知OH最小即OH⊥BC时，由直角三角形面积公式即可得出结果．
答案详解：解：∵四边形ABCD是菱形，
∴AC⊥BD，BO＝DO＝4，OA＝CO，
∴BD＝8，
∵S菱形ABCD=12AC•BD＝24，
∴AC=2412BD=2412×8=6，
∴OA＝CO＝3，
由勾股定理得：BC=CO2+BO2=32+42=5，
∵当OH最小时，OH⊥BC，
此时S△OBC=12BO•CO=12BC•OH，
∴OH=BO⋅COBC=4×35=2.4，
即OH最小值为2.4，
所以答案是：2.4．
11．已知四边形ABCD为菱形，∠BAD＝60°，AB＝6cm，P为AC上任一点，则PD+12PA的最小值是 33 cm．
试题分析：根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC于P，过P点作PH⊥AB，将12PA转化为PH，当PDH三点在同一直线时，PD+12PA＝PH取最小值．可得答案．
答案详解：解：过P点作PH⊥AB，
∵四边形ABCD为菱形，∠BAD＝60°，
∴∠DAC＝30°，
∴PH=12PA，
又∵菱形的对角线互相垂直平分，可得B、D关于AC对称，连接PB．则PD＝PB，
∴PD+12PA＝PD+PH
即当P，D，H三点在同一直线时，PD+12PA＝PH取最小值．
∵∠BAD＝60°，AD＝AB＝6，
∴△ABD是等边三角形，
过D点作DH'⊥AB，
∵AH'＝BH'＝3，
在△AD'H中，DH'=AD2−H'A2=62−32=33，即 最小值为33．
所以答案是：33．
12．如图，在平面直角坐标系xOy中，点A的坐标为（0，12），点B为x轴上一动点，以AB为边在直线AB的右侧作等边三角形ABC．若点P为OA的中点，连接PC，则PC的长的最小值为 9 ．
试题分析：以AP为边作等边三角形APE，连接BE，过点E作EF⊥AP于F，由“SAS”可证△ABE≌△ACP，可得BE＝PC，则当BE有最小值时，PC有最小值，即可求解．
答案详解：解：如图，以AP为边作等边三角形APE，连接BE，过点E作EF⊥AP于F，
∵点A的坐标为（0，12），
∴OA＝12，
∵点P为OA的中点，
∴AP＝6，
∵△AEP是等边三角形，EF⊥AP，
∴AF＝PF＝3，AE＝AP，∠EAP＝∠BAC＝60°，
∴∠BAE＝∠CAP，
在△ABE和△ACP中，
AE=AP∠BAE=∠CAPAB=AC，
∴△ABE≌△ACP（SAS），
∴BE＝PC，
∴当BE有最小值时，PC有最小值，
即BE⊥x轴时，BE有最小值，
∴BE的最小值为OF＝OP+PF＝6+3＝9，
∴PC的最小值为9，
所以答案是：9．
13．如图，AB＝3，P为平面内一动点，且PA＝2，以PB为边在PB上方作等边三角形PBM，连接MA，则MA的最小值为 1 ．
试题分析：把△PBA绕点P逆时针旋转60°得△PMC，连接AC，由旋转的性质得出MC＝3，AC＝2，由三角形的三边关系得出1≤MA≤5，进而求出MA的最小值是1．
答案详解：解：如图，
∵△PBM是等边三角形，
∴把△PBA绕点P逆时针旋转60°得△PMC，连接AC，
∴MC＝AB＝3，PC＝AP＝2，∠APC＝60°，
∴△APC是等边三角形，
∴AC＝AP＝2，
∴3﹣2≤MA≤3+2，即1≤MA≤5，
∴MA的最小值是1，
所以答案是：1．
14．如图，在正方形ABCD中，AB＝5，点E在边CD上，且CE＝2，在边BC上取两点M，N（点M在点N左侧），且始终保持MN＝1，线段MN在边BC上平移，则AM+EN的最小值为 65 ．
试题分析：作A点关于BC的对称点G，连接MG，过点G作GH∥MN，过点N作NH∥MG，当E、N、H三点共线时，AM+NE有最小值，过点H作HK⊥CD交延长线于点K，求出EH即为所求．
答案详解：解：作A点关于BC的对称点G，连接MG，过点G作GH∥MN，过点N作NH∥MG，
∴四边形MGHN是平行四边形，
∴NH＝MG＝AM，
∴AM+NE＝NH+NE，
当E、N、H三点共线时，AM+NE有最小值，
过点H作HK⊥CD交延长线于点K，
∵AB＝5，CE＝2，
∴EK＝7，
∵MN＝1，
∴GH＝1，
∴HK＝4，
在Rt△HKE中，EH=65，
∴AM+EN的最小值为65，
所以答案是：65．
15．如图，四边形ABCD是矩形，点E是边AB上的一动点，连接DE，点A与点P关于DE对称，连接EP、DP、BP，若AB＝3，BC＝4，则BP的最小值为 1 ．
试题分析：连接BD，AP，由四边形ABCD是矩形得∠A＝90°，根据勾股定理求出BD的长为5，再根据轴对称的性质求得PD＝AD＝4，根据两点之间线段最短列不等式BP+4≥5，得BP≥5﹣4，可知BP的最小值为5﹣4．
答案详解：解：如图，连接BD，AP，
∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝3，BC＝AD＝4，
∴BD=AB2+AD2=32+42=5，
∵点A与点P关于DE对称，
∴DE垂直平分AP，
∴PD＝AD＝4，
∵BP+PD≥BD，
∴BP+4≥5，
∴BP≥5﹣4＝1，
∴BP的最小值为1，
所以答案是：1．
16．如图，在矩形ABCD中，AB＝2，AD＝1，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（ ）
A．2B．4C．2D．22
试题分析：根据中位线定理可得出点点P的运动轨迹是线段P1P2，再根据垂线段最短可得当BP⊥P1P2时，PB取得最小值；由矩形的性质以及已知的数据即可知BP1⊥P1P2，故BP的最小值为BP1的长，由勾股定理求解即可．
答案详解：解：如图：
当点F与点C重合时，点P在P1处，CP1＝DP1，
当点F与点E重合时，点P在P2处，EP2＝DP2，
∴P1P2∥CE且P1P2=12CE．
当点F在EC上除点C、E的位置处时，有DP＝FP．
由中位线定理可知：P1P∥CE且P1P=12CF．
∴点P的运动轨迹是线段P1P2，
∴当BP⊥P1P2时，PB取得最小值．
∵矩形ABCD中，AB＝2，AD＝1，E为AB的中点，
∴△CBE、△ADE、△BCP1为等腰直角三角形，CP1＝1．
∴∠ADE＝∠CDE＝∠CP1B＝45°，∠DEC＝90°．
∴∠DP2P1＝90°．
∴∠DP1P2＝45°．
∴∠P2P1B＝90°，即BP1⊥P1P2，
∴BP的最小值为BP1的长．
在等腰直角BCP1中，CP1＝BC＝1．
∴BP1=2．
∴PB的最小值是2．
所以选：C．
17．如图，在四边形中ABCD，∠ABC＝∠ADC＝90°，E是对角线AC的中点，F是对角线BD上的动点，连接EF．若AC＝6，BD＝4，则EF的最小值为 5 ．
试题分析：连接BE，DE，根据直角三角形斜边的中线的性质可得BE＝DE，过点E作EF′⊥BD于点F′，可知BF′的长度，根据勾股定理求出EF′的长，即可确定EF的最小值．
答案详解：解：连接BE，DE，如图所示：
∵∠ABC＝∠ADC＝90°，E是对角线AC的中点，
∴BE=12AC，DE=12AC，
∵AC＝6，
∴BE＝DE＝3，
过点E作EF′⊥BD于点F′，
则点F′是线段BD的中点，
∵BD＝4，
∴BF′＝2，
根据勾股定理，得EF′=32−22=5，
∴线段EF的最小值为5，
所以答案是：5．
18．在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE的最小值是 3013 ．
试题分析：当CM⊥AB时，CM的值最小，此时DE的值也最小，根据勾股定理求出AB，根据三角形的面积求出CM，再求出答案即可．
答案详解：解：如图，连接CM，
∵点D、E分别为CN，MN的中点，
∴DE=12CM．
当CM⊥AB时，CM的值最小，此时DE的值也最小．
由勾股定理得：AB=AC2+BC2=52+122=13．
∵S△ABC=12•AB•CM=12•AC•BC，
∴CM=6013．
∴DE=12CM=3013．
所以答案是：3013．