高教版（2021·十四五）基础模块 下册5.5 指数函数与对数函数的应用优质课件ppt

这是一份高教版（2021·十四五）基础模块 下册5.5 指数函数与对数函数的应用优质课件ppt，共14页。PPT课件主要包含了指数函数模型，对数函数模型等内容，欢迎下载使用。

2008年3月，在福布斯全球财富排行榜上，77岁的美国人沃伦·巴菲特成为了全球首富.而在1962年，巴菲特的个人资产仅有100万美元.46年来，他依靠在股票、外汇等市场上的投资，平均年增长率约达27.11%，到2008年，作为全球首富的巴菲特究竟拥有多少资产呢？
1962 年，资产 100 万1963 年，资产100 + 100 × 27.11% = 100（1 +27.11%）万1964年 ， 资 产 100(1 + 27.11%) + 100(1 +27.11%) × 27.11 = 100(1 + 27.11%)(1 + 27.11%) =100（1 + 27.11%）2万 …… ……2008 年，资产100（1 + 27.11%）46万
使用指数型函数f(x)=abx+c(a,b,c为常数,a>0,b>1)所表达的函数模型，其特点是随着自变量x的增大，函数值增长的速度越来越快，也称为“指数激增”。
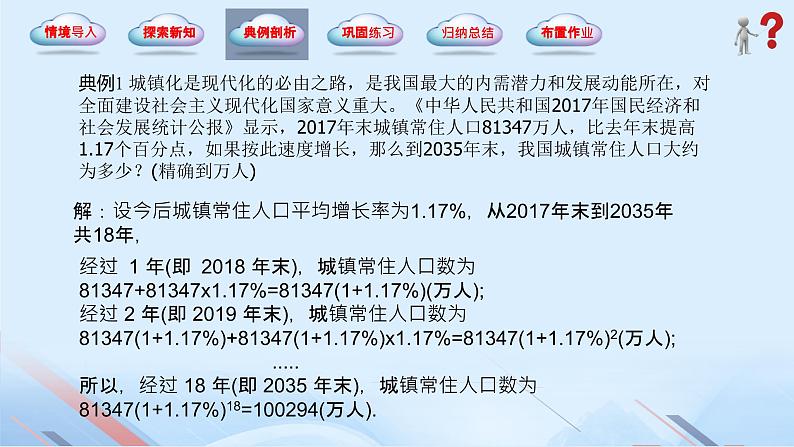
典例1 城镇化是现代化的必由之路，是我国最大的内需潜力和发展动能所在，对全面建设社会主义现代化国家意义重大。《中华人民共和国2017年国民经济和社会发展统计公报》显示，2017年末城镇常住人口81347万人，比去年末提高1.17个百分点，如果按此速度增长，那么到2035年末，我国城镇常住人口大约为多少？(精确到万人)
解：设今后城镇常住人口平均增长率为1.17%，从2017年末到2035年共18年，
经过 1 年(即 2018 年末)，城镇常住人口数为 81347+81347x1.17%=81347(1+1.17%)(万人); 经过 2 年(即 2019 年末)，城镇常住人口数为 81347(1+1.17%)+81347(1+1.17%)x1.17%=81347(1+1.17%)2(万人); 所以，经过 18 年(即 2035 年末)，城镇常住人口数为81347(1+1.17%)18=100294(万人).
典例2 目前某县有100万人．经过x年后为y万人．如果年平均增长率是1.2%.请回答下列问题：(1)写出y关于x的函数解析式；(2)计算10年后该县的人口总数(精确到0.1万人).
解： (1)当x＝1时，y＝100＋100×1.2%＝100(1＋1.2%)当x＝2时，y＝100(1＋1.2%)＋100(1＋1.2%)×1.2%＝100(1＋1.2%)2；当x＝3时，y＝100(1＋1.2%)2＋100(1＋1.2%)2×1.2%＝100(1＋1.2%)3；……故y关于x的函数解析式为y＝100(1＋1.2%)x(x∈N*)．
(2)当x＝10时，y＝100(1＋1.2%)10＝100×1.01210≈112.7，故10年后该县人口总数约有112.7万人．
用对数型函数f(x)=mlgax(m,n,a为常数，m>0,x>0,a>1)表达的函数模型，其特点是开始阶段增长得较快，但随着x的增大，函数值变化得越来越慢，也称“蜗牛式增长”。
[解析]　设该林区的森林原有蓄积量为a，由题意ax＝a(1＋0.104)y，故y＝lg1.104x(x≥1)，所以y＝f(x)的图象大致为D中图象．