高教版（中职）基础模块下册(2021)5.5 指数函数与对数函数的应用公开课教学ppt课件

这是一份高教版（中职）基础模块下册(2021)5.5 指数函数与对数函数的应用公开课教学ppt课件，共17页。PPT课件主要包含了学习目标，投资问题，做出三种函数的图像，课堂小结，解释说明等内容，欢迎下载使用。

第五章 指数函数和对数函数 5.5 指数、对数函数的应用
在初中，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
例1. 假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下：①. 每天回报40元.②. 第一天回报10元，以后每天比前一天多回报10元.③. 第一天回报0.4元，以后每天的回报比前一天翻一番.
请问你会选择哪种投资方案？
①. 每天回报40元.
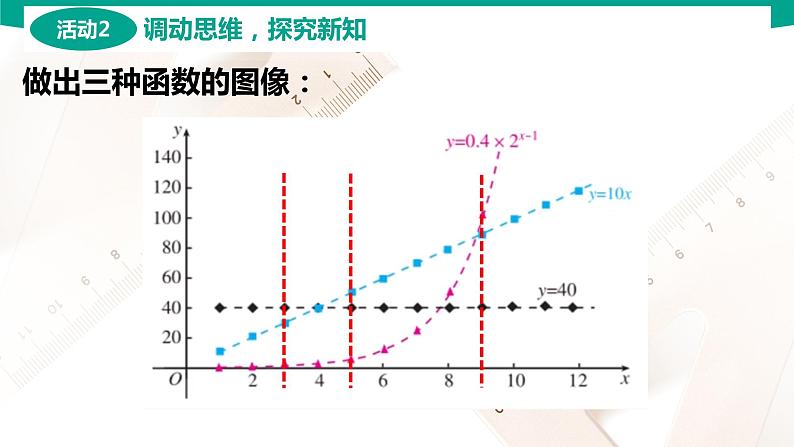
设x天所得的回报是y元，则方案一可以用函数：
②. 第一天回报10元,以后每天比前一天多回报10元.
则方案②可以用函数：y=10x(x∈N+)进行描述.
③. 第一天回报0.4元，以后每天的回报比前一天翻一番.
y=40(x∈N+) 进行描述.
则方案③可以用函数：y=0.4×2x-1(x∈N+)进行描述.
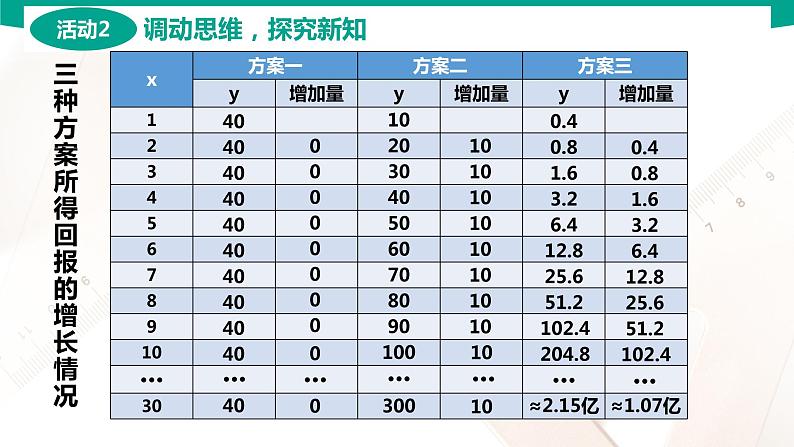
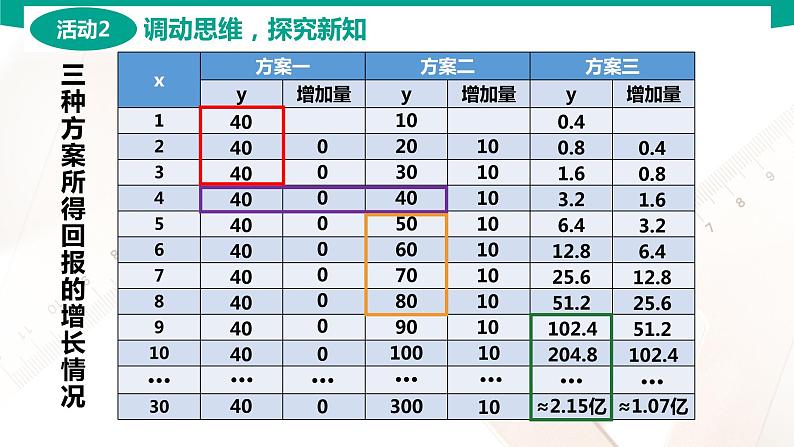
三种方案所得回报的增长情况
问：仅仅分析每天的回报能准确的做出选择吗？
根据刚才的分析，是不是5天以下选方案一，5-8天选方案二，8天以上选方案三？
思考：划分天数的标准是什么？
我们将累计回报数制成表格：
根据表格，我们得出投资方案如下：
投资7天以下，应选择方案一，投资7天，选择方案一或方案二，投资8-10天，应选择方案二，投资10天以上，应选择方案三.
例2：某公司为了实现1000万元的利润目标，准备制定一个激励销售人员的奖励方案，在销售利润达到10万元时，按销售利润进行奖励，且奖金y(万元)随销售利润x的增加而增加，但奖金总数不超过5万元，同时奖金不超过利润的25%，现有三个奖励模型：①. y=0.25x，②. y=lg7x+1，③. y=1.002x问：其中哪个模型符合公司的要求？
分析：奖金不会超过公司的利润，所以奖金x的取值范围是：[10,1000]，对应的奖金y满足2个条件：
即：x∈[10,1000]时，①. 奖金总数y≤5②. 奖金不超过利润的25%，即y≤0.25x.
借助信息技术画出三个函数的图像：
下面通过计算确认上述判断：
方案①. y=0.25x，当x=20时，y=5，
而y=0.25x在[10,1000]上单调递增，
方案③. y=1.002x，利用信息技术可知：
而y=1.002x在[10,1000]上单调递增，
当x＞20时，y＞5，所以该模型不符合要求.
存在一个数a∈[805,806]，使1.002a=5，
当x＞a时，y＞5，所以该模型也不符合要求.
方案②. y=lg7x+1，在区间[10,1000]上单调递增，
当x=1000时，y=lg71000+1≈4.55＜5，
要求2. x∈[10,1000]时是否有y≤0.25x ？
若y≤0.25x,则lg7x+1≤0.25x,即lg7x+1-0.25x≤0
所以该模型符合总奖金不超过5万元的要求.
令f(x)=lg7x+1-0.25x,利用信息技术画图f(x)的图像
有图像可知，f(x)在区间[10,1000]上单调递减，
因此f(x)≤f(10)≈-0.32＜0
即lg7x+1≤0.25x，所以该模型满足公司的要求.