




初中数学冀教版八年级下册第二十二章 四边形22.6 正方形图文ppt课件
展开1.掌握正方形的所有性质,理解正方形、菱形、矩形、平行四边形之间的关系2.能掌握正方形不同的判定方法,能根据已知条件选择正确的方法判定正方形
观察下列图片,有你熟悉的四边形吗?
问题1:回忆小学时学过的内容,说一说你对正方形有哪些认识?
四条边相等、四个角都是直角的四边形
问题2:四边都相等的四边形是我们学过的什么图形?四个角都是直角的四边形是什么图形?正方形与它们有什么关系?
四条边都相等的四边形是菱形;
四个角都是直角的四边形是矩形;
所以正方形既是矩形又是菱形.
讨论:既然正方形既是矩形,又是菱形,试从边、角、对角线三个方面说一说正方形的所有性质.
正方形的对边相等且平行,四条边都相等;
对角相等,且四个角都相等,都为直角;
对角线相等且互相垂直平分.
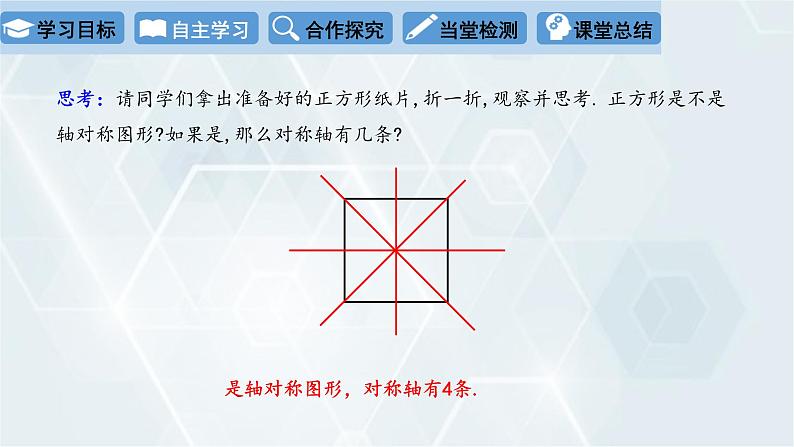
思考:请同学们拿出准备好的正方形纸片,折一折,观察并思考. 正方形是不是轴对称图形?如果是,那么对称轴有几条?
是轴对称图形,对称轴有4条.
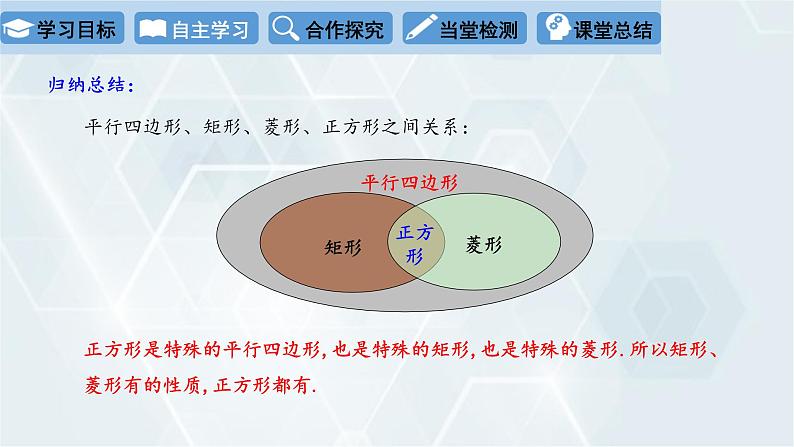
平行四边形、矩形、菱形、正方形之间关系:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
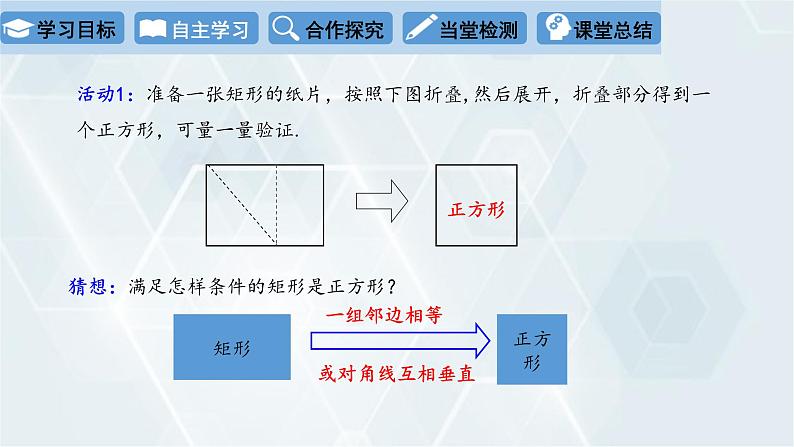
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证.
猜想:满足怎样条件的矩形是正方形?
已知:如图,在矩形ABCD中,AC,DB是它的两条对角线,AC⊥DB.求证:四边形ABCD是正方形.
结论:对角线互相垂直的矩形是正方形.
证明:∵四边形ABCD是矩形,
∴AO=CO=BO=DO,
∴AD=CD=BC=AB,
∴四边形ABCD是正方形.
∴△AOD≌△COD≌△BOC≌△AOB
问题3:观察下列图形变化过程,想一想满足怎样条件的菱形是正方形?
有一个角是直角的菱形是正方形.
(或对角线相等的菱形是正方形)
已知:如图,在菱形ABCD中,AC,DB是它的两条对角线,AC=DB.求证:四边形ABCD是正方形.
结论:对角线相等的菱形是正方形.
证明:∵四边形ABCD是菱形(即是平行四边形),AC=BD,
∴四边形ABCD是矩形,
正方形判定的两条途径:
探究一 正方形性质的运用
问题提出:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证: △ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
(1)题中已知一个正方形,你能说说边和对角线都有些什么性质吗?
四条边相等,对角线相等且互相平分即AB=BC=CD=AD,AC=BD,AC⊥BD,AO=BO=CO=DO.
(2)在通过三角形的全等判定方法即可得证.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形
∴△ABO≌ △BCO ≌ △CDO ≌ △DAO.
又∵ AD=CD=BC=AB
结论:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
1.如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE交CD于F,求∠AFC的度数.
解:∵四边形ABCD是正方形,
∴∠ACB=45°,∠DCB=∠DCE=90°,
∵∠ACB是△ACE的外角,
∵∠AFC是△CFE的外角,
∴∠AFC=∠FCE+∠E=90°+22.5°=112.5°
探究二 正方形判定的运用
问题提出:在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?
(2)题中已知AE=BF=CM=DN,对你解题有什么启发?
可证明四个三角形全等,即△AEN≌△BFE≌△CMF≌△DNM,从而得到四边形EFMN的四条边相等,得出四边形EFMN是菱形.
(3)根据三角形内角和的计算,再依据“有一个角是直角的菱形是正方形”即可得证.
(1)题中给出正方形,说一说它的边和角有什么性质.
正方形的对边平行,四条边相等,四个角相等且都是直角.
探究二 正方形判定的运用
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
在△AEN、△BFE、△CMF、△DNM中,
∴AN=BE=CF=DM.
AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
∴四边形EFMN是正方形 (有一个角是直角的菱形是正方形).
2.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD,(1)判断四边形OCED是什么特殊四边形,证明你的结论.
四边形OCED是菱形.
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又∵在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)当AB、AD满足什么条件时,四边形OCED是正方形?请说明理由.
当AB=AD时,四边形OCED是正方形.
∴矩形ABCD是正方形,
∴AC⊥BD,即OC⊥OD,
∴菱形ABCD是正方形.
1.一个正方形的对角线长为2 cm,则它的面积是 ( )A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
2.已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.求证:(1)四边形FBGH是菱形;
证明:∵点F、G是边AC的三等分点,
又∵点D是边AB的中点,
∴四边形FBGH是平行四边形,
连结BH,交AC于点O,
∴四边形FBGH是菱形.
2.已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.求证:(2)四边形ABCH是正方形.
证明:(2)∵四边形FBGH是平行四边形,
由(1)已证:AO=CO,
∴四边形ABCH是平行四边形,
∵∠ABC=90°,AB=BC,
∴四边形ABCH是正方形.
初中数学冀教版八年级下册第二十二章 四边形22.6 正方形优秀ppt课件: 这是一份初中数学冀教版八年级下册第二十二章 四边形22.6 正方形优秀ppt课件,文件包含226正方形课件ppt、226正方形教案doc等2份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
冀教版八年级下册第二十二章 四边形22.6 正方形获奖课件ppt: 这是一份冀教版八年级下册第二十二章 四边形22.6 正方形获奖课件ppt,文件包含226正方形课件ppt、226正方形教案doc等2份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
冀教版八年级下册22.6 正方形一等奖课件ppt: 这是一份冀教版八年级下册22.6 正方形一等奖课件ppt,文件包含河北教育版数学八年级下·226正方形教学课件pptx、226正方形教案docx、226正方形同步练习docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













