










中考数学一轮复习考点(精讲精练)复习专题15 函数与其他实际运用问题(2份打包,原卷版+教师版)
展开
这是一份中考数学一轮复习考点(精讲精练)复习专题15 函数与其他实际运用问题(2份打包,原卷版+教师版),文件包含中考数学一轮复习考点精讲精练复习专题15函数与其他实际运用问题原卷版doc、中考数学一轮复习考点精讲精练复习专题15函数与其他实际运用问题原卷版pdf、中考数学一轮复习考点精讲精练复习专题15函数与其他实际运用问题教师版doc、中考数学一轮复习考点精讲精练复习专题15函数与其他实际运用问题教师版pdf等4份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
知识导航
题型精讲
题型一:拱桥类问题
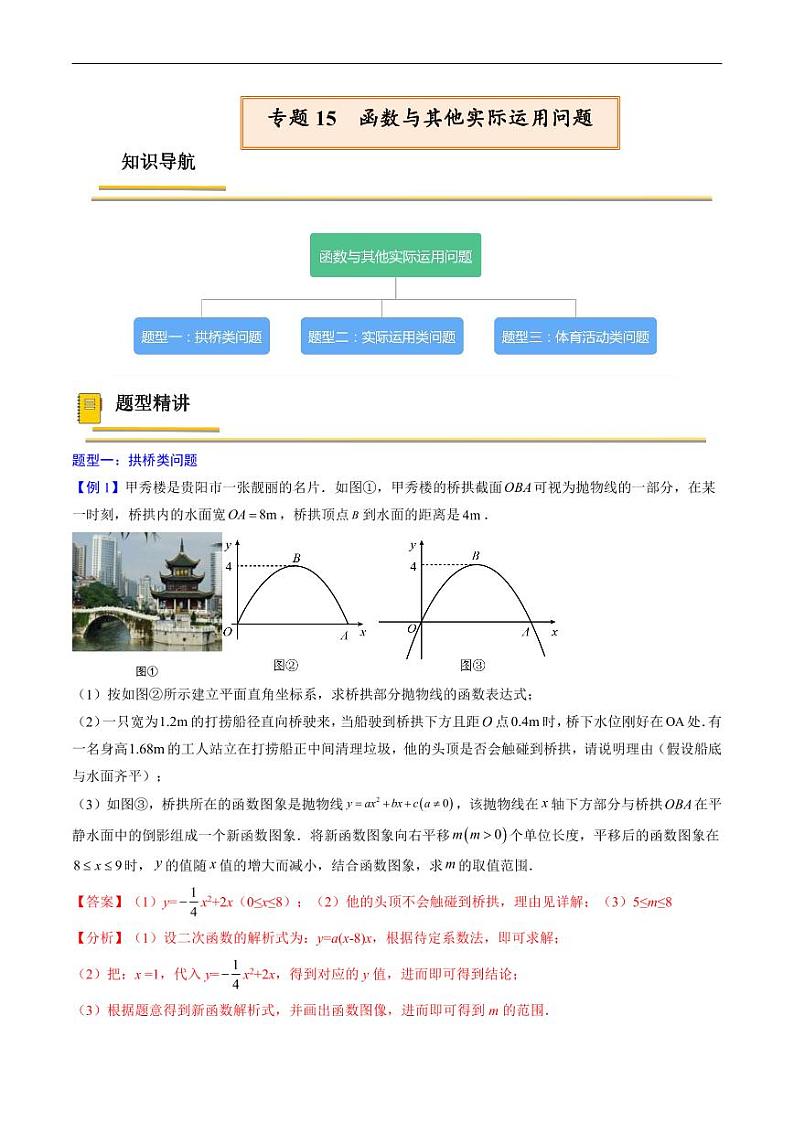
【例1】甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 SKIPIF 1 < 0 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 SKIPIF 1 < 0 ,桥拱顶点 SKIPIF 1 < 0 到水面的距离是 SKIPIF 1 < 0 .
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为 SKIPIF 1 < 0 的打捞船径直向桥驶来,当船驶到桥拱下方且距 SKIPIF 1 < 0 点 SKIPIF 1 < 0 时,桥下水位刚好在 SKIPIF 1 < 0 处.有一名身高 SKIPIF 1 < 0 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);
(3)如图③,桥拱所在的函数图象是抛物线 SKIPIF 1 < 0 ,该抛物线在 SKIPIF 1 < 0 轴下方部分与桥拱 SKIPIF 1 < 0 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 SKIPIF 1 < 0 个单位长度,平移后的函数图象在 SKIPIF 1 < 0 时, SKIPIF 1 < 0 的值随 SKIPIF 1 < 0 值的增大而减小,结合函数图象,求 SKIPIF 1 < 0 的取值范围.
【答案】(1)y= SKIPIF 1 < 0 x2+2x(0≤x≤8);(2)他的头顶不会触碰到桥拱,理由见详解;(3)5≤m≤8
【分析】(1)设二次函数的解析式为:y=a(x-8)x,根据待定系数法,即可求解;
(2)把:x =1,代入y= SKIPIF 1 < 0 x2+2x,得到对应的y值,进而即可得到结论;
(3)根据题意得到新函数解析式,并画出函数图像,进而即可得到m的范围.
【详解】(1)根据题意得:A(8,0),B(4,4),设二次函数的解析式为:y=a(x-8)x,
把(4,4)代入上式,得:4=a×(4-8)×4,解得: SKIPIF 1 < 0 ,
∴二次函数的解析式为:y= SKIPIF 1 < 0 (x-8)x= SKIPIF 1 < 0 x2+2x(0≤x≤8);
(2)由题意得:x=0.4+1.2÷2=1,代入y= SKIPIF 1 < 0 x2+2x,得y= SKIPIF 1 < 0 ×12+2×1= SKIPIF 1 < 0 >1.68,
答:他的头顶不会触碰到桥拱;
(3)由题意得:当0≤x≤8时,新函数表达式为:y= SKIPIF 1 < 0 x2-2x,
当x<0或x>8时,新函数表达式为:y=- SKIPIF 1 < 0 x2+2x,
∴新函数表达式为: SKIPIF 1 < 0 ,∵将新函数图象向右平移 SKIPIF 1 < 0 个单位长度,
∴ SKIPIF 1 < 0 (m,0), SKIPIF 1 < 0 (m+8,0), SKIPIF 1 < 0 (m+4,-4),如图所示,
根据图像可知:当m+4≥9且m≤8时,即:5≤m≤8时,平移后的函数图象在 SKIPIF 1 < 0 时, SKIPIF 1 < 0 的值随 SKIPIF 1 < 0 值的增大而减小.
题型二:实际运用类问题
【例2】如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体 SKIPIF 1 < 0 处,另一端固定在离地面高2米的墙体 SKIPIF 1 < 0 处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度 SKIPIF 1 < 0 (米)与其离墙体 SKIPIF 1 < 0 的水平距离 SKIPIF 1 < 0 (米)之间的关系满足 SKIPIF 1 < 0 ,现测得 SKIPIF 1 < 0 , SKIPIF 1 < 0 两墙体之间的水平距离为6米.
图2
(1)直接写出 SKIPIF 1 < 0 , SKIPIF 1 < 0 的值;
(2)求大棚的最高处到地面的距离;
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为 SKIPIF 1 < 0 米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
【答案】(1) SKIPIF 1 < 0 , SKIPIF 1 < 0 ;(2) SKIPIF 1 < 0 米;(3)352
【分析】(1)根据题意,可直接写出点A点B坐标,代入 SKIPIF 1 < 0 ,求出b、c即可;
(2)根据(1)中函数解析式直接求顶点坐标即可;
(3根据 SKIPIF 1 < 0 ,先求得大棚内可以搭建支架的土地的宽,再求得需搭建支架的面积,最后根据每平方米需要4根竹竿计算即可.
【详解】解:(1)由题意知点A坐标为 SKIPIF 1 < 0 ,点B坐标为 SKIPIF 1 < 0 ,
将A、B坐标代入 SKIPIF 1 < 0 得: SKIPIF 1 < 0 解得: SKIPIF 1 < 0 ,故 SKIPIF 1 < 0 , SKIPIF 1 < 0 ;
(2)由 SKIPIF 1 < 0 ,可得当 SKIPIF 1 < 0 时, SKIPIF 1 < 0 有最大值 SKIPIF 1 < 0 ,
即大棚最高处到地面的距离为 SKIPIF 1 < 0 米;
(3)由 SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,又因为 SKIPIF 1 < 0 ,
可知大棚内可以搭建支架的土地的宽为 SKIPIF 1 < 0 (米),
又大棚的长为16米,故需要搭建支架部分的土地面积为 SKIPIF 1 < 0 (平方米)
共需要 SKIPIF 1 < 0 (根)竹竿.
题型三:体育活动类问题
【例3】2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点作水平线的垂线为轴,建立平面直角坐标系.图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点正上方米处的点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离处的水平距离为米时,离水平线的高度为米,求抛物线的函数解析式(不要求写出自变量的取值范围);
(2)在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过米时,求的取值范围.
【答案】(1);(2)12米;(3).
【分析】(1)根据题意可知:点A(0,4)点B(4,8),利用待定系数法代入抛物线即可求解;
(2)高度差为1米可得可得方程,由此即可求解;
(3)由抛物线可知坡顶坐标为 ,此时即当时,运动员运动到坡顶正上方,若与坡顶距离超过米,即,由此即可求出b的取值范围.
【详解】解:(1)根据题意可知:点A(0,4),点B(4,8)代入抛物线得,
,解得:,∴抛物线的函数解析式;
(2)∵运动员与小山坡的竖直距离为米,∴,
解得:(不合题意,舍去), ,
故当运动员运动水平线的水平距离为12米时,运动员与小山坡的竖直距离为米;
(3)∵点A(0,4),∴抛物线,
∵抛物线,∴坡顶坐标为 ,
∵当运动员运动到坡顶正上方,且与坡顶距离超过米时,
∴,解得:.
提分训练
1.(2021·浙江)如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
【答案】(1)6m;(2)①;②2m
【分析】(1)设,由题意得,求出抛物线图像解析式,求当x=12或x=-12时y1的值即可;
(2)①由题意得右边的抛物线顶点为,设,将点H代入求值即可;
②设彩带长度为h,则,代入求值即可.
【详解】解(1)设,由题意得,,,
,当时,,桥拱顶部离水面高度为6m.
(2)①由题意得右边的抛物线顶点为,设,
,,,,(左边抛物线表达式:)
②设彩带长度为h,则,当时,,
答:彩带长度的最小值是2m .
2.下图是某同学正在设计的一动画示意图,轴上依次有,,三个点,且,在上方有五个台阶(各拐角均为),每个台阶的高、宽分别是1和1.5,台阶到轴距离.从点处向右上方沿抛物线:发出一个带光的点.
(1)求点的横坐标,且在图中补画出轴,并直接指出点会落在哪个台阶上;
(2)当点落到台阶上后立即弹起,又形成了另一条与形状相同的抛物线,且最大高度为11,求的解析式,并说明其对称轴是否与台阶有交点;
(3)在轴上从左到右有两点,,且,从点向上作轴,且.在沿轴左右平移时,必须保证(2)中沿抛物线下落的点能落在边(包括端点)上,则点横坐标的最大值比最小值大多少?
(注:(2)中不必写的取值范围)
【答案】(1),见解析,点会落在的台阶上;(2),其对称轴与台阶有交点;(3).
【分析】(1)二次函数与坐标轴的交点坐标可以直接算出,根据点的坐标可以确定轴,利用函数的性质可以判断落在那个台阶上;
(2)利用二次函数图象的平移来求解抛物线,再根据函数的对称轴的值来判断是否与台阶有交点;
(3)抓住二次函数图象不变,是在左右平移,要求点横坐标的最大值比最小值大多少,利用临界点法,可以确定什么时候横坐标最大,什么时候横坐标最小,从而得解.
【详解】解:(1)当,,解得:,
在左侧,,关于对称,轴与重合,如下图:
由题意在坐标轴上标出相关信息,当时,,解得:,
,∴点会落在的台阶上,坐标为,
(2)设将抛物线,向下平移5个单位,向右平移的单位后与抛物线重合,则抛物线的解析式为:,
由(1)知,抛物线过,将代入,,
解得:(舍去,因为是对称轴左边的部分过),抛物线:,
关于,且,其对称轴与台阶有交点.
(3)由题意知,当沿轴左右平移,恰使抛物线下落的点过点时,此时点的横坐标值最大;
当,,解得:(取舍),故点的横坐标最大值为:,
当沿轴左右平移,恰使抛物线下落的点过点时,此时点的横坐标值最小;
当,,解得:(舍去),故点的横坐标最小值为:,
则点横坐标的最大值比最小值大:,故答案是:.
3.如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 SKIPIF 1 < 0 与注水时间 SKIPIF 1 < 0 之间的关系如图②所示,根据图象解答下列问题:
(1)图②中折线 SKIPIF 1 < 0 表示_____________槽中水的深度与注入时间之间的关系;线段 SKIPIF 1 < 0 表示_____________槽中水的深度与注入时间之间的关系;铁块的高度为_____________ SKIPIF 1 < 0 .
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)
【答案】(1)乙,甲,16;(2)2分钟
【分析】(1)根据图象分析可知水深减少的图象为甲槽的,水深增加的为乙槽的,并水深16cm之后增加的变慢,即可得到铁块的高度;
(2)利用待定系数法求出两个水槽中水深与时间的解析式,即可求解.
【详解】解:(1)图②中折线 SKIPIF 1 < 0 表示乙槽中水的深度与注入时间之间的关系;
线段 SKIPIF 1 < 0 表示甲槽中水的深度与放出时间之间的关系;铁块的高度为16 SKIPIF 1 < 0 .
(2)设甲槽中水的深度为 SKIPIF 1 < 0 ,把 SKIPIF 1 < 0 , SKIPIF 1 < 0 代入,可得
SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 ,∴甲槽中水的深度为 SKIPIF 1 < 0 ,
根据图象可知乙槽和甲槽水深相同时,在DE段,
设乙槽DE段水的深度为 SKIPIF 1 < 0 ,把 SKIPIF 1 < 0 , SKIPIF 1 < 0 代入,可得
SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 ,∴甲槽中水的深度为 SKIPIF 1 < 0 ,
∴甲、乙两个水槽中水的深度相同时, SKIPIF 1 < 0 ,解得 SKIPIF 1 < 0 ,
故注入2分钟时,甲、乙两个水槽中水的深度相同.
相关试卷
这是一份中考数学一轮复习考点(精讲精练)复习专题16 探究函数图象与性质问题(2份打包,原卷版+教师版),文件包含中考数学一轮复习考点精讲精练复习专题16探究函数图象与性质问题原卷版doc、中考数学一轮复习考点精讲精练复习专题16探究函数图象与性质问题原卷版pdf、中考数学一轮复习考点精讲精练复习专题16探究函数图象与性质问题教师版doc、中考数学一轮复习考点精讲精练复习专题16探究函数图象与性质问题教师版pdf等4份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
这是一份中考数学一轮复习考点(精讲精练)复习专题11 函数图象的分析与辨析(2份打包,原卷版+教师版),文件包含中考数学一轮复习考点精讲精练复习专题11函数图象的分析与辨析原卷版doc、中考数学一轮复习考点精讲精练复习专题11函数图象的分析与辨析原卷版pdf、中考数学一轮复习考点精讲精练复习专题11函数图象的分析与辨析教师版doc、中考数学一轮复习考点精讲精练复习专题11函数图象的分析与辨析教师版pdf等4份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
这是一份中考数学一轮复习考点(精讲精练)复习专题07 一次函数(2份打包,原卷版+教师版),文件包含中考数学一轮复习考点精讲精练复习专题07一次函数原卷版doc、中考数学一轮复习考点精讲精练复习专题07一次函数原卷版pdf、中考数学一轮复习考点精讲精练复习专题07一次函数教师版doc、中考数学一轮复习考点精讲精练复习专题07一次函数教师版pdf等4份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。









