2022-2023学年湖北省襄阳市樊城区八年级下学期期中数学试题及答案

这是一份2022-2023学年湖北省襄阳市樊城区八年级下学期期中数学试题及答案，共28页。

A.2，3，4B.C.1，2，2D.5，12，13
如图，在平面直角坐标系中▱OABC的顶点O，A，B的坐标分别是，，，则点C的坐标是()
A.
B.
C.
D.
菱形的两条对角线的长分别是4cm和6cm，则菱形的面积是()
A.B.C.D.
如图，正方形ABCD的边长为4，N为AD上一点，连接BN，于点M，连接CM，若，则的面积为
()
A.5
B.6
C.7
D.8
如图1，四边形ABCD 中，，，点P从点A出发，以每秒1个单位长度的速度，按的顺序在边上匀速运动，设P点的运动时间为t s，
的面积为S，S关于t的函数图象如图2所示.当点P运动到BC的中点时，的面积为()
A.7B.C.8D.
已知四边形ABCD的对角线交于点O，下列哪组条件能判断四边形ABCD是平行四边形()
A.，
B.，
C.，
D.，
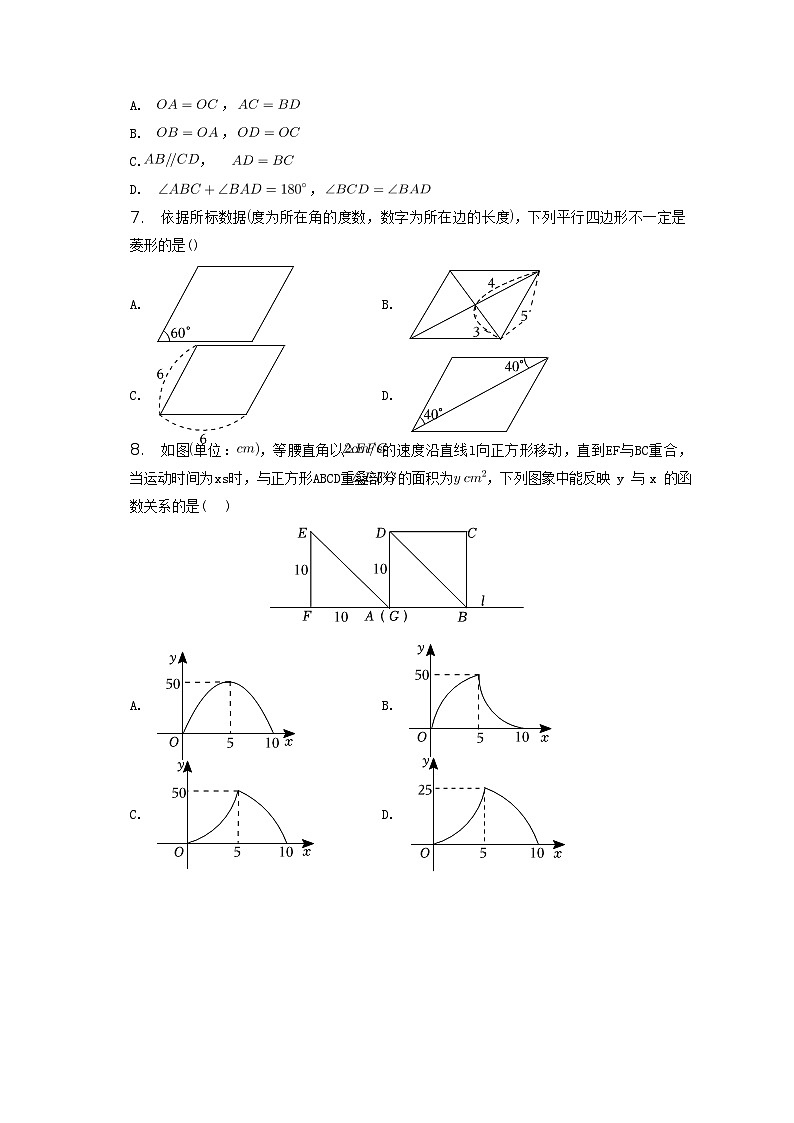
依据所标数据度为所在角的度数，数字为所在边的长度，下列平行四边形不一定是菱形的是()
A.B.
C.D.
如图单位：，等腰直角以的速度沿直线l向正方形移动，直到EF与BC重合，当运动时间为xs时，与正方形ABCD重叠部分的面积为，下列图象中能反映 y 与 x 的函数关系的是( )
A.B.
C.D.
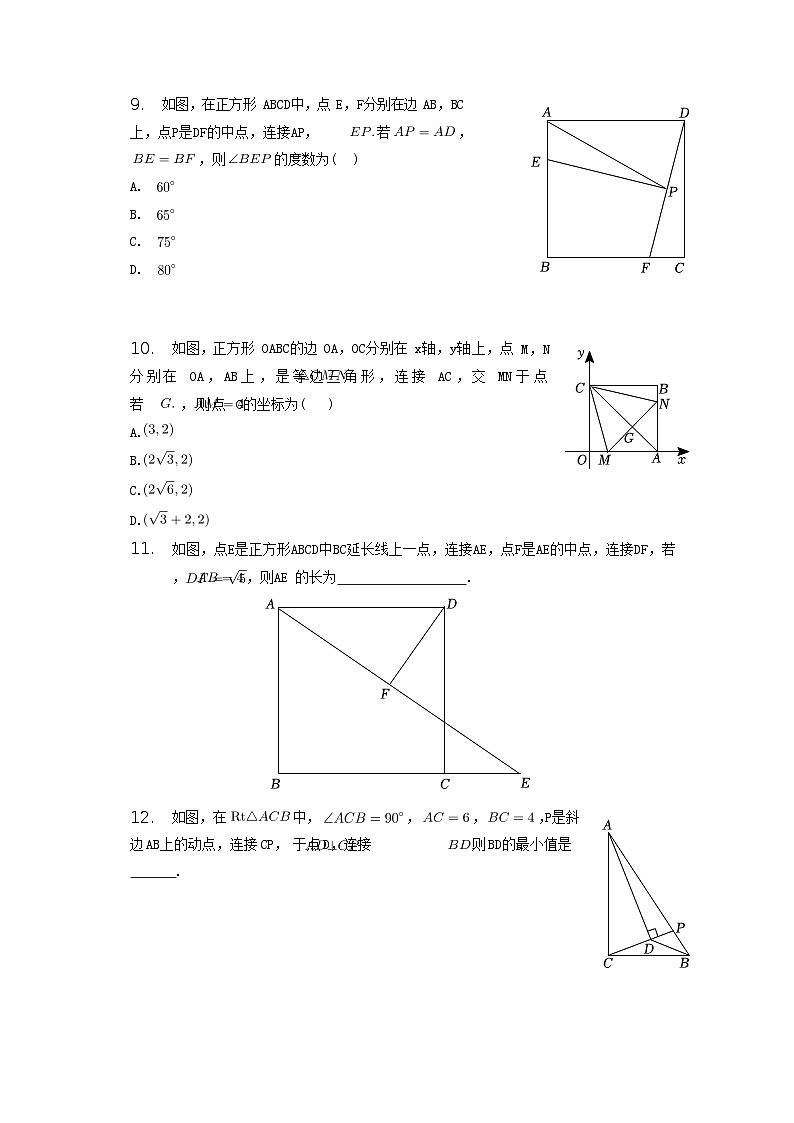
如图，在正方形 ABCD中，点 E，F分别在边 AB，BC
上，点P是DF的中点，连接AP，若，
，则的度数为()
A.
B.
C.
D.
如图，正方形 OABC的边 OA，OC分别在 x轴，y轴上，点 M，N分别在 OA，AB上，是等边三角形，连接 AC，交 MN于点 若 ，则点 G的坐标为( )
A.
B.
C.
D.
如图，点E是正方形ABCD中BC延长线上一点，连接AE，点F是AE的中点，连接DF，若，，则AE 的长为.
如图，在中，，，，P是斜边AB上的动点，连接CP，于点D，连接则BD的最小值是
.
如图，在平面直角坐标系中，直线：与直线交于点，过作x 轴的垂线，垂足为，过作的平行线交于，过作x轴的垂线，垂足
为，过作的平行线交于，过作x 轴的垂线，垂足为…按此规律，则点的纵坐标为.
在平面直角坐标系中，以任意两点，为端点的线段的中点坐标为 在直角坐标系中，有，，三点，另有一点D 与A， B，C 构成平行四边形的顶点，则点D 的坐标为.
如图，中，AD是角平分线，AE是中线，
于P，，，则PE的长为.
如图，O为矩形ABCD的对角线AC的中点，过O作分别交AD，BC于点
E，
求证：四边形 AFCE是菱形；
若，，求菱形AFCE的面积.
如图，在平行四边形ABCD中，于点E，延长DA至点F，使得
，连接 BF，
求证：EF平行且等于 BC；
求证：四边形 BCEF是矩形；
若，，，求EC的长.
计算：
；
已知，，求的值.
如图，在平面直角坐标系中，直线与x轴、y轴分别交于点A、点B，与直线CD：交于点P，
求直线 CD的解析式；
连接OP、BC，若直线AB 上存在一点Q，使得，求点Q 的坐标； 将直线 CD向下平移 1个单位长度得到直线，直线 l与 x轴交于点 E，点 N为直线 l上的一点，在平面直角坐标系中，是否存在点 M，使以点 O，E，N，M 为顶点的四边形是矩形？若存在，请直接写出点 M 的坐标；若不存在，请说明理由.
如图，在平面直角坐标系中，直线与x轴交于点，与y轴交于点
A，直线过点A，与x轴交于点C，点P是x轴上方一个动点. 求直线 AB 的函数表达式；
若点P在线段AB上，且，求点P的坐标；
当时，动点M从点B出发，先运动到点P，再从点P运动到点C后停
止运动.点M的运动速度始终为每秒1个单位长度，运动的总时间为秒，请直接写出t的最小值.
在平面直角坐标系xOy 中，直线：与x轴交于点A，与y轴交于点当时，；当时，
求k，b的关系式用含b的代数式表示； 若
①求直线的解析式；
②若直线：与直线相交，且两条直线所夹的锐角为，求m的值.
如图1，已知函数与x轴交于点A，与y轴交于点B，点C与点A关于y
轴对称.
求直线 BC的函数解析式；
设点 M是 x轴上的一个动点，过点 M作 y轴的平行线，交直线 AB于点 P，交直线 BC
于点
①若的面积为，求点M的坐标；
②连接BM，如图2，若，求点P的坐标.
答案和解析
【答案】D
【解析】解：A、因为，不能构成直角三角形，此选项不符合题意； B、因为，不能构成直角三角形，此选项不符合题意；C、因为，不能构成直角三角形，此选项不符合题意；
D、因为，能构成直角三角形，此选项符合题意．
故选：
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
【答案】C
【解析】解：四边形OABC是平行四边形， ，，即轴，
，A，B的坐标分别是，，，
，点 C与点 B的纵坐标相等，都为 3，
点C 的横坐标为，点C 的坐标为，
故选：
根据坐标与图形性质以及平行四边形的性质求解即可．
本题考查了平行四边形的性质、坐标与图形，熟练掌握坐标与图形的性质是解答的关键．
【答案】B
【解析】解：菱形的两条对角线的长分别为4cm和6cm，
面积为，
故选：
根据菱形的面积公式即可求解．
本题主要考查菱形的面积，解题的关键是熟知菱形的面积等于对角线乘积的一半．
【答案】B
【解析】解：作于点E，则，于点M，
，
四边形 ABCD是边长为 4的正方形，
，，
，
，，
，
，
，
，
故选：
的面积为 6，
作于点E，根据勾股定理求得，由
，得，则，所以，即
可求得的面积为
此题重点考查正方形的性质、勾股定理、锐角三角函数与解直角三角形、三角形的面积公式等知识，正确地作出所需要的辅助线并且求得是解题的关键．
【答案】A
【解析】解：根据题意得：四边形 ABCD是梯形，
当点P 从C 运动到D 处需要2 秒，则，面积为4，则，
根据图象可得当点P 运动到B 点时，面积为10，则，则运动时间为5 秒，
，
设当时，函数解析式为， ，
解得，
当时，函数解析式为，当P 运动到BC 中点时时间，
则，
故选：
首先结合图形和函数图象判断出CD的长和AD的长，进而可得AB的长，从而可得E点坐标，然后再计算出当时直线解析式，然后再代入t 的值计算出s 即可．
本题主要考查了动点问题的函数图象、三角形面积公式，利用数形结合的思想方法是解决问题的关键．
【答案】D
【解析】解：A、由，，不能判定四边形ABCD是平行四边形，故选项A
不符合题意；
B、由，，不能判定四边形ABCD是平行四边形，故选项B不符合题意； C，由，，不能判定四边形ABCD是平行四边形，故选项C不符合题意； D、，，
，，
，
四边形 ABCD是平行四边形，故选项 D符合题意；故选：
由平行四边形的判定分别对各个选项进行判断即可．
本题考查了平行四边形的判定以及平行线的判定，掌握平行四边形的判定是解题的关键．
【答案】A
【解析】解：平行四边形的一个角为，不能确定边的长度，不一定是菱形，该选项符合题意；
四边形是平行四边形，
B.因为，对角线相互垂直，因为对角线互相垂直的平行四边形是菱形，所以该选项正确，不符合题意；
对边相等，故 B不一定是菱形；
C.平行四边形对边平行，又邻边相等，所以平行四边形的四边相等，一定是菱形，所以该选项正确，不符合题意；
D.由图可知平行边四形的邻边相等，所以平行四边形的四边相等，一定是菱形，所以该选项正确，不符合题意；
故选：
根据菱形的判定解答即可．
此题主要考查了菱形的判定以及平行四边形的性质，解答本题的关键是根据菱形的判定方法解答．
【答案】C
，
【解析】解：如图1，当时重叠部分为三角形，面积
，
如图2，当时，重叠部分
为梯形，面积，
图象为两段二次函数图象，纵观各选项，只有 C选项符合．故选：
分别求出时与时的函数解析式，然后根据相应的函数图象找出符合条件的选项即可
本题考查了动点问题的函数图象，判断出重叠部分的形状并求出相应的函数关系式是解题的关键．
【答案】C
【解析】解：如图，过点A作于H，连接DE、CP、BP、EF，
四边形 ABCD是正方形，
，点 P是 DF的中点，
， ， ，
≌，
，
，，，
，
，
是等边三角形，
，
，
，，
，，，
， ，
，
即，
≌，
，，
，
是等边三角形， ，
点 P是 DF的中点，
，
，，
是等腰直角三角形， ，
故选：
如图，过点A作于H，连接DE、CP、BP、EF，由正方形性质可得：
，，，利用直角三角形斜边上的中线等于斜边一半可得：，进而可证得≌，可推出是等边三角形，得出：，，再由等腰三角 形性质可得，再证明≌，推出是等边三角
形，得出，再由是等腰直角三角形，得出，即可求得答案．
本题是四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的性质，直角三角形性质等，添加辅助线构造全等三角形是解题关键，是一道常
见的中考数学选择题压轴题．
【答案】B
【解析】解：如图，过点G作于H，
四边形 ABCO是正方形，
是等边三角形， ，
，
，，，
，
，
即，
，，
，
，
是等边三角形，，
，
，
，
是等腰直角三角形，，
，
，点 G 的坐标为
故选：
如图，过点G作于H，利用正方形性质和等边三角形性质可证得
，得出，推出，利用等腰直角三角形性质和等边三角形性质即可求得答案．
本题考查了正方形的性质，等边三角形性质，等腰直角三角形性质，全等三角形的判定和性质，
解直角三角形等知识，知识点较多，综合性强，是常考题型，熟练掌握相关性质是解题关键．
【答案】
【解析】解：过F作分别交AD、BC于
G，H，则四边形 GDCH为矩形，
，，
，四边形 ABCD是正方形，
，，
是 AE的中点，
，
在与中，
，
≌，
，，
在中，，
，，
， ，
在中，，
故答案为：
根据正方形的性质得出，进而利用AAS 证明与全等，进而利用全等三角形的性质和勾股定理解答即可．
此题考查正方形的性质，关键是根据正方形的四边相等和勾股定理解答．
【答案】2
【解析】解：取 AC中点 M，连接 MD，MB， ，
，
，
的最小值是故答案为：
，，，
，
，
取 AC中点 M，连接 MD，MB，由直角三角形的性质求出 DM的长，由勾股定理求出 BM的长，由三角形的三边关系即可求出 BD 的最小值．
本题考查直角三角形斜边的中线，三角形三边的关系，勾股定理，关键是通过作辅助线构造
，应用三角形的三边关系定理求 BD的最小值．
将表达式与直线的表达式联立并解得：，，即点的纵坐标为；
同理可得的纵坐标为，
…按此规律，则点的纵坐标为，故答案为：
联立直线与直线的表达式并解得：，，故，依次求出：点的纵坐标为、的纵坐标为，即可求解．
本题考查了两直线的交点，要求利用图象求解各问题，要认真体会点的坐标，一次函数与二元一次方程组之间的内在联系．
【答案】或或
13.【答案】
【解析】解：联立直线与直线的表达式并解得：
，
，故；
则点，则直线的表达式为：
将点坐标代入上式并解得：直线的表达式为：
，
，
【解析】解：如图，分三种情况：
①当AB 为对角线，，时， ，，，
把B向左平移2个单位，再向下平移2个单位，得D点坐标为，
②当BC 为对角线，，时， ，，，，
由线段中点坐标公式得：的坐标为；
③当AC为对角线，，时，由线段中点坐标公式得的坐标为；
综上所述，符合要求的点D的坐标为或或，故答案为：或或
分三种情况：①当 AB为对角线时，②当 BC为对角线时，③当 AC为对角线时，分别由平行四边形的判定以及中点坐标公式即可得出结论．
本题考查了平行四边形的判定、坐标与图形性质以及分类讨论等知识，熟练掌握平行四边形的判定和中点坐标公式是解题的关键．
【答案】1
【解析】解：如图所示，延长 CP交 AB于点 F，
中，AD是角平分线， ，
，
，
又，
≌，
，，
则，
又AE 是中线，则， 是的中位线， ，
故答案为：
延长 CP交 AB于点 F，证明 P为 CF的中点，进而根据三角形中位线的性质即可求解．本题考查了中位线的性质与判定，掌握三角形中位线的性质与判定是解题的关键．
【答案】证明：点O 是AC 的中点，，是AC 的垂直平分线，
，，，四边形 ABCD 是矩形，
，
在和中，
，
≌，
，
，四边形 AECF 为菱形．
解：设，则，四边形ABCD 是矩形，
在中，由勾股定理得，，即，
解得，，即，
，
菱形AFCE的面积=矩形ABCD的面积的面积的面积
【解析】根据线段垂直平分线的性质，可得，，，然后由四边形ABCD 是矩形，易证得≌，则可得，继而证得结论；
由勾股定理可求 BE，AC 的长，由直角三角形的性质可求解．
本题考查了矩形的性质，全等三角形的判定和性质，菱形的判定，证得≌是关键．
【答案】证明：四边形ABCD是平行四边形， ，，
， ，，
即 EF平行且等于 BC；
证明：由知，，；四边形 BCEF 是平行四边形，
又，
，
平行四边形 BCEF是矩形；
解：四边形ABCD是平行四边形，
，
，，
，
是直角三角形，，
的面积，
，
由得：，四边形BCEF是矩形，
，
【解析】由平行四边形的性质得，，再由，得， ；
证得四边形BCEF 是平行四边形，再证，即可得出结论；
由勾股定理的逆定理证是直角三角形，，再由面积法求出，然后由矩形的性质求解即可．
本题考查了矩形的判定与性质、平行四边形的判定与性质、勾股定理和勾股定理的逆定理以及三角形面积等知识；熟练掌握矩形的判定与性质是解题的关键．
【答案】解：原式；
原式
【解析】先化为最简二次根式，再利用二次根式加减法的运算法则计算求解； 利用二次根式乘除法的运算法则计算即可．
本题考查了二次根式的混合运算，熟练掌握运算法则和运算顺序是解题的关键．
【答案】解：，， ，，
【解析】先求xy、的值，再整体代入计算即可．
本题考查了二次根式的化简求值，掌握运算法则是解题的关键．
【答案】解：直线与x轴、y轴分别交于点A、点B，令，则，
点A为，，
，
点C为，点D为，设直线CD的解析式为；
， ，
直线CD的解析式为；
解：在中，令，则，
点B为，
，
解得，
点P的坐标为；
；
，点 P的坐标为
，
，
，
，
，
解得：
，
，
点Q在直线AB上，则设点Q为，则当点 Q 在点 B 的下方时，如图：
点Q的坐标为；当点 Q在点 P的上方时，如图：
， ，
解得：， ，
点Q的坐标为；
综合上述，点Q的坐标为或；
解：直线CD向下平移1个单位长度得到直线l，
直线l为，
令，则，点E的坐标为，
即；
当作为矩形OEMN的边时，如图：
点N的坐标为，
点M的坐标为；
当作为矩形OEMN的对角线时，如图：
点F的坐标为，
， ， ，
是等腰直角三角形， ，
四边形 ONEM是正方形，
，，
，
点M的坐标为；
综合上述，则点M的坐标为或；
【解析】先求出OA，然后求出点C 和点D 的坐标，利用待定系数法，即可求出解析式；先求出点 B和点 P的坐标，然后求出四边形 OBCP的面积，然后分类讨论：当点 Q在点 B的下方时；当点 Q 在点 P 的上方时；分别求出三角形 PQC 的面积，即可求出点 Q 的坐标；
先求出直线l 为，然后得到，然后分情况进行分析：当作为矩形 OEMN 的边时；当作为矩形OEMN的对角线时；分别求出两种情况的点M的坐标即可．本题考查了矩形的性质，一次函数的图象和性质，坐标与图形，等腰直角三角形的性质等知识，解题的关键是熟练掌握所学的知识，正确的作出图形，从而运用分类讨论的思想进行解题．
【答案】解：点A在y轴上，直线过点A，点A 坐标为，
将点和点代入直线，得，
解得，
直线AB的函数表达式为；
设点P 坐标为， 令，得，
点C坐标为，
点，点， ，，，
，点 P 在线段 AB 上，
， ，
，
解得，
点P坐标为；
设点P纵坐标为，
，点 P是 x轴上方的一个动点，点 P 与点 A 纵坐标相同，
，
解得，
作点B关于直线的对称点，连接，交直线于点P，连接BP，
点 M的运动速度始终为每秒 1个单位长度，
，的最小值为
【解析】先根据直线过点A，求出点A坐标，再利用待定系数法求直线AB的函数表达式即可；
设点P 坐标为，先求出点C 坐标，再求出的面积，表示出的面积，根据，列方程求解即可；
根据，点P是x轴上方的一个动点，可知点P在直线上运动，作点B
关于直线的对称点，连接，交直线于点P，连接BP，则的最小值
则
的最小值即为
的长，
点 B
点
坐标为，
坐标为，
，
即为的长，求出的长度，进一步可得t的最小值．
本题考查了一次函数的综合题，涉及待定系数法求解析式，轴对称的性质，三角形面积等，本题综合性较强，熟练三角形求面积的方法是解题的关键．
【答案】解：当时，；当时，，当时，，即，
， ，
，b的关系式为；
①如图：
由知，， ， ，
， ，
把，代入得：
，
解得，
直线的解析式为；
②设直线与x 轴交于D，连接BD，直线与直线交于C，当C 在y 轴左侧时，过C 作轴于H，如图：
在中，令得， ，
，，
，，， ，
， ，
是等腰直角三角形，
，
在中，，
，
当C在y轴右侧时，过C作轴于K，如图：
，，
是等腰直角三角形，
，
，
，
把
代入
得：
解得
，
；
，
，
， ， ，
在中，
，，
，
，
把代入得： ，
解得，
综上所述，两条直线所夹的锐角为，m的值为或
【解析】根据当时，；当时，，可得当时，，即
，即可得k，b的关系式为；
①由，，可得，用待定系数法即可得直线的解析式为
；②设直线与x轴交于D，连接BD，直线与直线交于C，分两种情况：当C 在y 轴左侧时，过C 作轴于H，由可得，即可得 ，故，从而是等腰直角三角形，由
，可得，代入得；当C在y
轴右侧时，过C作轴于K，由是等腰直角三角形，有
，而，即可得，代入得
本题考查一次函数的综合应用，涉及待定系数法，等腰直角三角形的性质及应用，含角的直角三角形三边关系等知识，解题的关键是分类讨论思想的应用．
【答案】解：在中，令得， ，
令得， ，
点 C与点 A关于 y轴对称，
，
设直线BC的解析式为，
，
解得，
直线BC的函数解析式为； ①设，
轴，
，，
， ，
解得，
的坐标为或；
②点 M在线段 AC上运动， ，
当点 M在线段 AO上时，如图：
点 C与点 A关于 y轴对称，
，
， ， ，
， ，
，
，
，，，
，
解得，
；
当点 M在线段 OC上时，如图：
同理可得，
综上所述：点P的坐标为或
【解析】分别求出A、B、C三点坐标，用待定系数法求函数的解析式即可；
①设，则，，求出，再由
，求出 m的值后即可求 M点坐标；
②分两种情况讨论：当点M 在线段AO 上时，利用角的关系推导出，再由勾股定理得，求出m的值即可求点P的坐标；当点M在线段OC上时，同理可求P 点的另一个坐标．
本题考查一次函数的综合应用，涉及待定系数法，三角形面积，勾股定理及应用等知识，解题的
关键是用含字母的式子表示相关点坐标和相关线段的长度．