

专题14 二次函数 中考数学一轮复习专题训练(北京专用)
展开1.(2021九上·平谷期末)用长为2米的绳子围成一个矩形,它的一边长为x米,设它的面积为S平方米,则S与x的函数关系为( )
A.正比例函数关系B.反比例函数关系
C.一次函数关系D.二次函数关系
2.(2021九上·石景山期末)正方形的面积y与它的周长x满足的函数关系是( )
A.正比例函数B.一次函数C.二次函数D.反比例函数
3.(2021九上·海淀期末)在平面直角坐标系xOy中,下列函数的图象经过点(0,0)的是( )
A.y=x+1B.y=x2C.y=(x−4)2D.y=1x
4.(2021九上·燕山期末)在求解方程ax2+bx+c=0(a≠0)时,先在平面直角坐标系中画出函数y=ax2+bx+c的图象,观察图象与x轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( )
A.x1=−3,x2=2B.x1=−3,x2=3
C.x1=−2,x2=2D.x1=−2,x2=3
5.(2021九上·密云期末)如图,一个矩形的长比宽多3cm,矩形的面积是Scm2.设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A.S=4x+6B.S=4x-6C.S=x2+3xD.S=x2-3x
6.(2021九上·昌平期末)关于二次函数y=-(x -2)2+3,以下说法正确的是( )
A.当x>-2时,y随x增大而减小B.当x>-2时,y随x增大而增大
C.当x>2时,y随x增大而减小D.当x>2时,y随x增大而增大
7.(2021九上·通州期末)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,关于a,c的符号判断正确的是( )
A.a>0,c>0B.a>0,c<0C.a<0,c>0D.a<0,c<0
8.(2021九上·大兴期末)将二次函数y=x2−4x+5用配方法化为y=(x−ℎ)2+k的形式,结果为( )
A.y=(x−4)2+1B.y=(x−4)2−1
C.y=(x−2)2−1D.y=(x−2)2+1
9.(2021九上·丰台期末)抛物线y=(x−4)2+1的对称轴是( )
A.x=4B.x=1C.x=−1D.x=−4
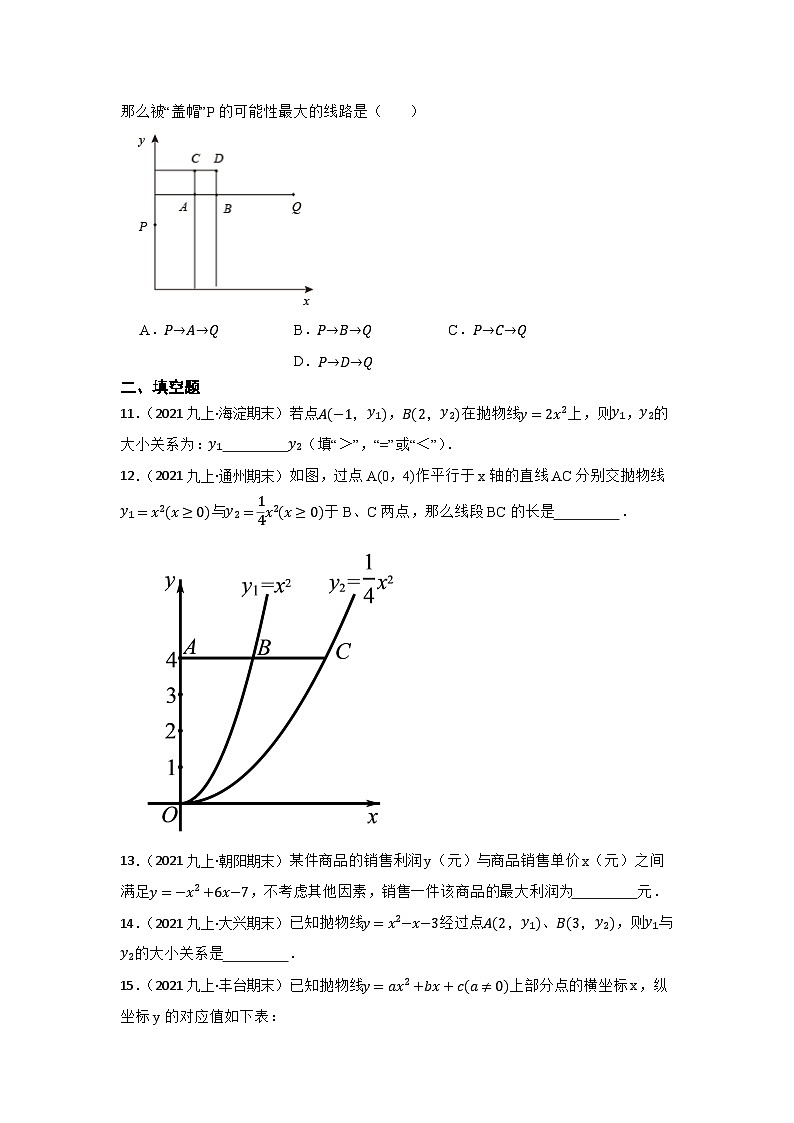
10.(2022九下·北京市开学考)在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”P的可能性最大的线路是( )
A.P→A→QB.P→B→QC.P→C→QD.P→D→Q
二、填空题
11.(2021九上·海淀期末)若点A(−1,y1),B(2,y2)在抛物线y=2x2上,则y1,y2的大小关系为:y1 y2(填“>”,“=”或“<”).
12.(2021九上·通州期末)如图,过点A(0,4)作平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=14x2(x≥0)于B、C两点,那么线段BC的长是 .
13.(2021九上·朝阳期末)某件商品的销售利润y(元)与商品销售单价x(元)之间满足y=−x2+6x−7,不考虑其他因素,销售一件该商品的最大利润为 元.
14.(2021九上·大兴期末)已知抛物线y=x2−x−3经过点A(2,y1)、B(3,y2),则y1与y2的大小关系是 .
15.(2021九上·丰台期末)已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如下表:
那么该抛物线的顶点坐标是 .
16.(2022九下·北京市开学考)如果抛物线y=3x2向下平移2个单位,所得到的抛物线是 .
17.(2021九上·丰台期末)中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩.某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分.如图所示,该运动员起跳点A距离水面10m,运动过程中的最高点B距池边2.5m,入水点C距池边4m,根据上述信息,可推断出点B距离水面 m.
18.(2021九上·顺义期末)若二次函数y=x2+bx+4配方后为y=(x−1)2+k,则b= , k= .
19.(2021九上·北京市月考)若二次函数y=2x2-3的图象上有两个点A(1,m),B(2,n),则m n(填“<”“=”或“>”).
20.(2021九上·平谷期末)某地的药材批发公司指导农民养植和销售某种药材,经市场调研发现1-8月份这种药材售价(元)与月份之间存在如下表所示的一次函数关系,同时,每千克的成本价(元)与月份之间近似满足如图所示的抛物线,观察两幅图表,试判断 月份出售这种药材获利最大.
三、综合题
21.(2021九上·海淀期末)在平面直角坐标系xOy中,点(4,3)在抛物线y=ax2+bx+3(a>0)上.
(1)求该抛物线的对称轴;
(2)已知m>0,当2−m≤x≤2+2m时,y的取值范围是−1≤y≤3,求a,m的值;
(3)在(2)的条件下,是否存在实数n,当n−2
(1)求抛物线的顶点坐标(用含m的式子表示);
(2)若x1=m−2,x2=m+2,比较y1与y2的大小,并说明理由;
(3)若对于−1≤x1<4,x2=4,都有y1≤y2,直接写出m的取值范围.
23.(2022九上·昌平期中)已知二次函数y=x2+2x−3.
(1)求该二次函数的图象的对称轴和顶点坐标;
(2)求该二次函数的图象与x轴交点.
24.(2021九上·昌平期末)在平面直角坐标系xOy中,点(1,m)和点(3,n)在二次函数y=x2+bx的图象上
(1)当m=-3时
①求这个二次函数的顶点坐标;
②若点(-1,y1),(a,y2)在二次函数的图象上,且y2>y1,则a的取值范围是 ▲ ;
(2)当mn<0时,求b的取值范围
25.(2021九上·西城期末)已知二次函数y=x2+4x+3.
(1)求此函数图象的对称轴和顶点坐标;
(2)画出此函数的图象;
(3)若点A(0,y1)和B(m,y2)都在此函数的图象上,且y1
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
27.(2022九上·昌平期中)在平面直角坐标系xOy中,抛物线y=ax2−2ax−3(a≠0)与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点P(4,0),Q(−1a,0).若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
28.(2022·房山模拟)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,-3),其顶点为P.
(1)求二次函数的解析式及P点坐标;
(2)当m≤x≤m+1时,y的取值范围是-4≤y≤2m,求m的值.
29.(2021九上·东城期末)为了改善小区环境,某小区决定在一块一边靠墙(墙长25m)的空地上修建一个矩形小花园ABCD,小花园一边靠墙,另三边用总长40m的栅栏围住,如下图所示.若设矩形小花园AB边的长为xm,面积为ym2.
(1)求y与x之间的函数关系式;
(2)当x为何值时,小花园的面积最大?最大面积是多少?
30.(2022九上·海淀期中)探照灯的内部可以看成是抛物线的一部分经过旋转得到的抛物曲面.其原理是过某一特殊点的光线,经抛物线反射后所得的光线平行于抛物线的对称轴,我们称这个特殊点为抛物线的焦点.若抛物线的表达式为y=ax2,则抛物线的焦点为(0,14a).如图,在平面直角坐标系xOy中,某款探照灯抛物线的表达式为y=14x2,焦点为F.
(1)点F的坐标是 ;
(2)过点F的直线与抛物线交于A,B两点,已知沿射线FA方向射出的光线,反射后沿射线AM射出,AM所在直线与x轴的交点坐标为(4,0).
① 画出沿射线FB方向射出的光线的反射光线BP;
②BP所在直线与x轴的交点坐标为 ▲ .
答案解析部分
1.【答案】D
【解析】【解答】解:设矩形的一边长为x米,则另一边长为2−2x2米,
则S=x×2−2x2=−x2+x
则S与x的函数关系为二次函数关系
故答案为:D
【分析】设矩形的一边长为x米,则另一边长为2−2x2米,根据矩形的面积公式可得S=x×2−2x2=−x2+x,即可得到答案。
2.【答案】C
【解析】【解答】解:∵正方形的周长为x,
∴正方形的边长为x4,
∴正方形的面积y=(x4)2=116x2;
故答案为:C.
【分析】先利用x的表达式求出正方形的边长,然后利用正方形的面积公式列出解析式y=(x4)2=116x2即可得到答案。
3.【答案】B
【解析】【解答】解:A.当x=0时,y=0+1=1,y=x+1图象过点(0,1),选项A不合题意;
B.当x=0时,y=02=0,y=x2图象过点(0,0),选项B合题意;
C.当x=0时,y=(0−4)2=16,y=(x−4)2图象过点(0,16),选项C不合题意;
D.当x=0时,y=1x无意义,选项D不合题意.
故答案为:B.
【分析】将点(0,0)分别代入各选项的解析式求解判断即可。
4.【答案】D
【解析】【解答】解:因为两个交点的横坐标可以看作是方程的近似解,两个交点的横坐标为:x1=−2,x2=3,
所以方程的近似解是x1=−2,x2=3.
故答案为:D.
【分析】利用二次函数图象求一元二次方程的近似根即可。
5.【答案】C
【解析】【解答】解:设矩形的宽为xcm,则长为(x+3)cm
由题意得:S=x(x+3)=x2+3x.
故答案为:C.
【分析】设矩形的宽为xcm,则长为(x+3)cm,根据矩形的面积公式可得S=x(x+3)=x2+3x.
6.【答案】C
【解析】【解答】解:∵y=−(x−2)2+3,
∴抛物线开口向下,对称轴为x=2,顶点坐标为(2,3),
∵二次函数的图象为一条抛物线,当x>2时,y随x的增大而减小,x<2时,y随x增大而增大
∴C符合题意,
故答案为:C.
【分析】由于抛物线开口向下,对称轴为x=2,可得当x>2时,y随x的增大而减小,x<2时,y随x增大而增大,据此逐一判断即可.
7.【答案】B
【解析】【解答】解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的左侧,
∴b>0,
∵抛物线与y轴交于负半轴,
∴c<0.
故答案为:B.
【分析】根据二次函数图象与系数的关系即可得出答案。
8.【答案】D
【解析】【解答】解:y=x2−4x+4+1=(x−2)2+1,
故答案为:D.
【分析】利用配方法将一般式化为顶点式即可。
9.【答案】A
【解析】【解答】解:抛物线y=(x−4)2+1的对称轴是直线x=4,
故答案为:A.
【分析】根据抛物线顶点式的解析式可得对称轴为直线x=4。
10.【答案】B
【解析】【解答】解:B、D两点,横坐标相同,而D点的纵坐标大于B点的纵坐标,显然,B点上升阶段的水平距离长;A、B两点,纵坐标相同,而A点的横坐标小于B点的横坐标,等经过.A点的篮球运行到与B点横坐标相同时,显然在B点上方,故B点上升阶段的水平距离长;同理可知C点路线优于A点路线,综上:P→B→Q是被“盖帽”的可能性最大的线路.
故答案为:B.
【分析】分类讨论投篮线路经过A、B、C、D四个点时篮球上升阶段的水平距离求解即可。
11.【答案】<
【解析】【解答】解:∵若点A(−1,y1),B(2,y2)在抛物线y=2x2上,
y1=2×(-1)2=2,y2=2×4=8,
∵2<8,
∴y1﹤y2.
故答案为:﹤.
【分析】根据抛物线的性质求解即可。
12.【答案】2
【解析】【解答】解:∵x≥0,则y=4y=x2解得x=2y=4,即B(2,4)
y=4y2=14x2解得x=4y=4,即C(4,4)
∴BC=4−2=2
故答案为:2
【分析】根据二次函数的图象分析即可得出答案。
13.【答案】2
【解析】【解答】解:y=−x2+6x−7
y=−(x−3)2+2
根据函数图象性质可知在x=3时,y最大且取值为2
故答案为:2.
【分析】将一般式化为顶点式,再利用抛物线的性质求解即可。
14.【答案】y
【解析】【解答】解:∵点A(2,y1)点B(3,y2)经过抛物线y=x2-x-3,
∴y1=22-2-3=1, y2=32-3-3=3,
∴y1<y2.
故答案为:y1<y2.
【分析】根据抛物线的解析式求出y1与y2的值,再求解即可。
15.【答案】(1,-4)
【解析】【解答】解:观察表格并由抛物线的图像与性质可知
该抛物线的对称轴为直线x=−1+32=1
∵顶点坐标在对称轴上
∴由表格可知该抛物线的顶点坐标为(1,-4)
故答案为:(1,-4).
【分析】观察表格并由抛物线的图像与性质可知该抛物线的对称轴,因为顶点坐标在对称轴上,即可得出答案。
16.【答案】y=3x2−2
【解析】【解答】解:由“上加下减”的原则可知,将抛物线 y=3x2向下平移2个单位,得到的抛物线是: y=3x2−2.
故答案是: y=3x2−2.
【分析】根据函数解析式平移的原则:上加下减,左加右减求解即可。
17.【答案】454
【解析】【解答】解:建立平面直角坐标系如图:
根据题意可知,点A的坐标为(3,10),点C的坐标为(5,0),抛物线的对称轴为直线x=3.5,
设抛物线的的解析式为y=ax2+bx+c,把上面信息代入得,
9a+3b+c=1025a+5b+c=0b−2a=3.5,
解得,a=−5b=35c=−50,
抛物线解析式为:y=−5x2+35x−50,
把x=3.5代入得,y=454;
故答案为:454
【分析】建立平面直角坐标系,再设抛物线的的解析式为y=ax2+bx+c,再求出抛物线的解析式,然后将x=3.5代入计算即可。
18.【答案】-2;3
【解析】【解答】解:∵y=(x−1)2+k=x2−2x+1+k,
∴b=−2,1+k=4,
解得k=3,
故答案为:-2;3.
【分析】利用配方法将二次函数的一般式化为顶点式即可。
19.【答案】<
【解析】【解答】因点A(1,m),B(2,n)在函数的图象上,则有 m=2×12−3=−1,n=2×22−3=5
所以m<n
【分析】先求出m=2×12−3=−1,再求出n=2×22−3=5,最后比较大小即可。
20.【答案】5
【解析】【解答】解:设每千克的售价是y元,月份为x,则可设y=kx+b
把(3,8),(6,6)代入得,3k+b=86k+b=6
解得,k=−23b=10
∴y=−23x+10
设每千克成本是z元,根据图象可设z=a(x−6)2+1
把(3,4)代入z=a(x−6)2+1,得a(3−6)2+1=4
∴a=13
∴z=13x2−4x+13
∴设利润为w,则有:
w=y−z=−23x+10−(13x2−4x+13)=−13(x−5)2+163
∵−13<0
∴w=−13(x−5)2+163有最大值,
∴当x=5时,w有最大值,
∴5月份出售这种药材获利最大.
故答案为:5
【分析】先求出售价的函数解析式y=−23x+10,再求出成本的函数解析式z=13x2−4x+13再设利润为w,列出函数解析式w=y−z=−23x+10−(13x2−4x+13)=−13(x−5)2+163,最后利用抛物线的性质求解即可。
21.【答案】(1)解:依题意,
∵ 抛物线y=ax2+bx+3过点(0,3),(4,3),
∴ 该抛物线的对称轴为直线x=2.
(2)解:∵ 抛物线y=ax2+bx+3对称轴为直线x=2,
∴−b2a=2,即b=−4a①.
∵m>0,
∴2−m<2<2+2m.
∵a>0,抛物线开口向上,
∴ 当x=2时,函数值在2−m≤x≤2+2m上取得最小值−1.
即 4a+2b+3=−1②.
联立①②,解得a=1,b=−4.
∴ 抛物线的表达式为y=x2−4x+3,即y=(x−2)2−1.
∵m>0,
∴ 当2−m≤x≤2时,y随x的增大而减小,当x=2−m时取得最大值,
当2≤x≤2+2m时,y随x的增大而增大,当x=2+2m时取得最大值,
∵对称轴为x=2,
∴x=2−m与x=2+m时的函数值相等.
∵2<2+m<2+2m,
∴ 当x=2+2m时的函数值大于当x=2+m时的函数值,即x=2−m时的函数值.
∴ 当x=2+2m时,函数值在2−m≤x≤2+2m上取得最大值3.
代入有4m2−1=3,舍去负解,得m=1.
(3)存在,n=1
【解析】【解答】解:(3)解:存在,n=1.
∵当n−2
①当n≤2时,n−2
∴x=n−2时,y有最大值,x=n时,y有最小值,
由题意可知:(n−2)2−4(n−2)+3=3n+5n2−4n+3=3n−3,解得:n=1,
故n=1,
②当n−2≥2时,n−2
∴x=n−2时,y有最小值,x=n时,y有最大值,
由题意可知:(n−2)2−4(n−2)+3=3n−3n2−4n+3=3n+5,此时n无解,
故不符合题意,
∴n=1.
【分析】(1)抛物线y=ax2+bx+3过点(0,3),(4,3),即可得出该抛物线的对称轴;
(2)根据抛物线y=ax2+bx+3对称轴为直线x=2,得出抛物线开口向上,当x=2时,函数值在2−m≤x≤2+2m上取得最小值−1.当2−m≤x≤2时,y随x的增大而减小,当x=2−m时取得最大值,当2≤x≤2+2m时,y随x的增大而增大,当x=2+2m时取得最大值,当x=2+2m时的函数值大于当x=2+m时的函数值,即x=2−m时的函数值.当x=2+2m时,函数值在2−m≤x≤2+2m上取得最大值3;
(3)存在,①当n≤2时,n−2
=(x−m)2−1
所以抛物线的顶点坐标为:(m,1)
(2)解:∵y=(x−m)2−1,
∴ 抛物线的对称轴为:直线x=m,
∵x1=m−2,x2=m+2,
∴m−2
∴P(x1,y1),Q(x2,y2)关于直线x=m对称,
∴y1=y2.
(3)解:m≤32
【解析】【解答】(3)解:当抛物线的对称轴x=m≤−1时,如图,
Q始终在P的上方,满足y1
当−1
当2m−4≤−1时,满足y1≤y2,
此时−1
【分析】(1)将二次函数解析式化为顶点事求解即可;
(2)分别将x1=m−2,x2=m+2,代入解析式求解即可;
(3)求出关于对称轴对称点,根据抛物线开口向上及y1≤y2求解即可。
23.【答案】(1)解:y=x2+2x−3
=(x+1)2−4,
∴二次函数的图象的对称轴为直线x=−1和顶点坐标为(−1,−4)
(2)解:令y=0,有x2+2x−3=0,
解得:x1=−3,x2=1,
∴该二次函数的图象与x轴交点为(−3,0),(1,0).
【解析】【分析】(1)利用配方法将二次函数的一般式化为顶点式y=(x+1)2−4,再求解即可;
(2)将y=0代入y=x2+2x−3可得x2+2x−3=0,再求出x的值即可。
24.【答案】(1)解:当m=-3时
①把点(1,-3)代入y=x2+bx,得b=-4,
二次函数表达式为y=x2 -4x=(x-2)2 -4
所以顶点坐标为(2,-4)
②a<−1或a>5
(2)解:将点(1,m),(3,n)代入y=x2+bx,可得m=1+b ,n=9+3b
当mn<0时,有两种情况:
①若m>0,n<0. 把m=1+b ,n=9+3b代入可得1+b>0,9+3b<0. 此时不等式组无解
②若m<0,n>0. 把m=1+b ,n=9+3b代入可得1+b<0,9+3b>0.解得-3<b<-1
所以-3<b<-1
【解析】【解答】解:(1)②根据题意得抛物线y=x2 -4x开口向上,对称轴为直线x=2,
∵y2>y1,
∴i)当点(-1,y1),(a,y2)在抛物线对称轴左侧时,有a<−1;
ii)当点(-1,y1),(a,y2)在抛物线对称轴两侧时,根据对称性可知a>5;
所以a的取值范围是:a<-1或a>5
故答案为:a<-1或a>5
【分析】(1)①把点(1,-3)代入y=x2+bx中求出b值,即得y=x2 -4x,再化为顶点式即可求解;
②分两种情况:i)当点(-1,y1),(a,y2)在抛物线对称轴左侧;ii)当点(-1,y1),(a,y2)在抛物线对称轴两侧时,据此分别求解即可;
(2) 将点(1,m),(3,n)代入y=x2+bx,可得m=1+b ,n=9+3b ,当mn<0时,有两种情况:①若m>0,n<0.②若m<0,n>0. ,据此分别建立不等式组并求解即可.
25.【答案】(1)解:∵抛物线解析式为y=x2+4x+3=(x+2)2−1,
∴抛物线对称轴为直线x=−2,顶点坐标为(-2,-1);
(2)解:列表如下:
函数图象如下所示:
(3)m<−4或m>0
【解析】【解答】解:(3)
由函数图象可知,当y1
【分析】(1)根据抛物线解析式即可得出答案;
(2)根据列表即可画出函数图象;
(3)由函数图象可知,当y1
∴设y=a(x−3)2+3,
∵y=a(x−3)2+3经过点(0,53 ),
∴53=a(0−3)2+3
解得∶a=−427,
∴y=−427(x−3)2+3=−427x2+89x+53,
∴y关于x的函数表达式为y=−427x2+89x+53
(2)解:该女生在此项考试中是得满分,理由如下∶
∵对于二次函数y=−427x2+89x+53,当y=0时,有−427x2+89x+53=0
∴4x2−24x−45=0,
解得∶x1=152, x2=−32 (舍去),
∵152>6.70,
∴该女生在此项考试中是得满分.
【解析】【分析】(1)设y=a(x−3)2+3,再将点(0,53)代入y=a(x−3)2+3可得53=a(0−3)2+3,求出a的值,即可得到二次函数的解析式;
(2)将y=0代入解析式y=−427x2+89x+53可得−427x2+89x+53=0,再求出x的值即可。
27.【答案】(1)(0,-3)
(2)解:∵x=−b2a=−−2aa=1;
∴B(2,−3)
(3)解:当抛物线过点P(4,0)时,a=38,
∴Q(−83,0).
此时,抛物线与线段PQ有两个公共点.
当抛物线过点Q(−1a,0) 时,a=1,
此时,抛物线与线段PQ有两个公共点.
∵抛物线与线段PQ恰有两个公共点,
∴38≤a≤1.
当抛物线开口向下时,a<−3.
综上所述,当38≤a≤1或a<−3时,抛物线与线段PQ恰有两个公共点.
【解析】【解答】解:(1)由题意抛物线y=ax2−2ax−3(a≠0)与y轴交于点A ,将x=0代入求出坐标为(0,−3);
【分析】(1)根据抛物线y=ax2−2ax−3(a≠0)与y轴交于点A即可直接写出点A的坐标;
(2)点A、B关于对称轴对称,即可求点B的坐标;
(3)根据点P(4,0),Q(−1a,0),若抛物线与线段PQ恰有两个公共点,结合函数图象,即可求a的取值范围。
28.【答案】(1)解:点A、C在二次函数的图象上,
∴1+b+c=0c=−3,
解得b=2c=−3,
∴二次函数的解析式为:y=x2+2x−3,
∵y=(x+1)2−4
∴顶点P的坐标为(−1,−4);
(2)解:m⩽x⩽m+1时,y的最小值为−4,
∴m⩽−1⩽m+1,即−2⩽m⩽−1,
①−2⩽m<−32时,y最大值=m2+2m−3,
由m2+2m−3=2m,解得:m=3(舍去),m=−3,
②当−32⩽m⩽−1时,y最大值=(m+1)2+2(m+1)−3,
由(m+1)2+2(m+1)−3=2m,
解得:m=0(舍去),m=−2(舍去),
综上:m的值为−3.
【解析】【分析】(1)将点A、C的坐标代入y=x2+bx+c求出b、c的值,再利用配方法将一般式化为顶点式可得点P的坐标;
(2)分两种情况:①−2⩽m<−32时,y最大值=m2+2m−3,②当−32⩽m⩽−1时,y最大值=(m+1)2+2(m+1)−3,再分别求解即可。
29.【答案】(1)解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
∵AB=x m,
∴BC=(40-2x)m,
∴花园的面积为:y=AB•BC=x•(40-2x)=-2x2+40x,
∵40-2x≤25,x+x<40,
∴x≥7.5,x<20,
∴7.5≤x<20,
∴y与x之间的函数关系式为:y=-2x2+40x(7.5≤x<20);
(2)解:∵y=−2(x−10)2+200,(7.5≤x<20)
∴ 当x=10时,ymax=200.
答:当x为10m时,小花园的面积最大,最大面积是200m2.
【解析】【分析】(1)根据AB=x m,BC=(40-2x)m,再利用y=AB•BC=x•(40-2x)=-2x2+40x即可得到答案;
(2)利用配方法将抛物线的解析式化为顶点式y=−2(x−10)2+200,再利用抛物线的性质求解即可。
30.【答案】(1)(0,1)
(2)解:①由题意可知抛物线y=14x2的对称轴是y轴,
∴经抛物线反射后所得的光线平行于抛物线的对称轴,即经抛物线反射后所得的光线平行于y轴,
∴AM∥y轴
∵AM所在的直线与x轴的交点坐标为(4,0),
∴A点的横坐标为4,纵坐标为y=14×42=4,
∴A(4,4),
①经抛物线反射后所得的光线平行于y轴,
∴BP∥y轴
∴画出沿射线FB方向射出的光线的反射光线BP,如下图所示:
;
②(-1,0)
【解析】【解答】(1)解:根据题意得y=14x2,a=14,
∴14a=1,
∴F(0,1),
故答案为:(0,1);
(2)②设直线AB的解析式为y=kx+b(k≠0),把A(4,4)、F(0,1)代入,
得4k+b=4b=1,
解得:k=34b=1
∴直线AB的解析式为y=34x+1,
由题意可知,直线AB与抛物线交于A、B两点,
把y=14x2代入y=34x+1
整理得x2−3x−4=0,
解得:x1=−1,x2=4,
∵点B在y轴的左侧,
∴B点的横坐标为−1,
∵BP∥y轴,
∴BP所在直线与x轴的交点坐标为(−1,0),
故答案为:(−1,0).
【分析】(1)根据题意先求出14a=1,再求点的坐标即可;
(2)①先求出 AM∥y轴 ,再求出 BP∥y轴 ,最后求解即可;
②利用待定系数法求出直线AB的解析式为y=34x+1,再求出B点的横坐标为−1,最后求点的坐标即可x
…
-2
-1
0
1
2
3
…
y
…
5
0
-3
-4
-3
0
…
月份
...
3
6
...
每千克售价
...
8
6
...
x
…
-4
-3
-2
-1
0
…
y=x2+4x+3
…
3
0
-1
0
3
…
专题19 圆 中考数学一轮复习专题训练(北京专用): 这是一份专题19 圆 中考数学一轮复习专题训练(北京专用),共38页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。
专题5 分式 中考数学一轮复习专题训练(北京专用): 这是一份专题5 分式 中考数学一轮复习专题训练(北京专用),共11页。试卷主要包含了单选题,填空题,计算题等内容,欢迎下载使用。
专题4 因式分解 中考数学一轮复习专题训练(北京专用): 这是一份专题4 因式分解 中考数学一轮复习专题训练(北京专用),共11页。试卷主要包含了单选题,填空题,计算题等内容,欢迎下载使用。












