浙江省杭州市临安市2023年六年级下学期数学小升初模拟试卷

这是一份浙江省杭州市临安市2023年六年级下学期数学小升初模拟试卷，共14页。试卷主要包含了仔细推敲，细心判断，反复思考，慎重选择，用心思考，认真填空，注意审题，用心计算，看清要求，动手操作，灵活运用，解决问题等内容，欢迎下载使用。

一、仔细推敲，细心判断。(每小题2分，共10分）
1．表示一个星期的气温变化情况，选用扇形统计图比较合适。（ ）
2．3÷23=13×23=29。（ ）
3．任何自然数都是它本身倒数的100％。（ ）
4．从家到学校，甲用15分钟，乙用20分钟，甲乙的速度比是3：4。（ ）
5．第一车间昨天出勤50人，缺勤2人，缺勤率是4％。（ ）
二、反复思考，慎重选择。(将正确答案的序号填在括号里。每小题2分，共10分）
6．6个连续的自然数，如果后面三个数的和为90，那么前面三个数的和为（ ）。
A．93B．86C．81D．90
7．有一种手表零件长5毫米，在设计图纸的长度是10厘米，图纸的比例尺是（ ）。
A．1：20B．20：1C．1：200D．200：1
8．一个圆锥和一个圆柱高相等，底面积之比为为3∶1，则体积比是（ ）。
A．3∶1B．1∶3C．1∶1D．9∶1
9．如下图所示，把底面直径4厘米的圆柱切成若干等份，拼成一个近似的长方体，这个长方体的表面积比原来增加40平方厘米。那么长方体的高是（ ）厘米。
A．4B．8C．10D．20
10．100克水中加入10克盐，那么盐的重量是盐水重量的（ ）
A．19B．110C．111D．911
三、用心思考，认真填空。(每小题2分，共20分）
11．如图，两个长方形重叠放在桌上，阴影部分的面积是4平方厘米，是大长方形面积的16，是小长方形的14，则大长方形和小长方形面积的最简整数比是 ： ，整个图形的面积是 平方厘米。
12．使用+-×÷或括号使得结果为24，题目：3 3 7 7，算式： 。
13．两个完全一样的 可以拼成一个平行四边形，因此一个 的面积是所拼成平行四边形面积的 。
14．将一个长30厘米、宽24厘米的长方形恰好分割成若干个相等的正方形而没有剩余，这个正方形的边长最长是 厘米．
15．一堆玉米成圆锥形，底面周长是18.84米，高1米，把它嵌入底面是2平方米的圆柱体容器中，能装 米高。
16．如下图，已知正方形ABCD的周长是40厘米，DE=6.4厘米，阴影部分的面积是 平方厘米。
17．把78∶1.5化成最简单的整数比是 ，比值是 。
18．把一个底面直径为5厘米，高为12厘米的圆柱体沿直径切割成两个半圆柱，表面积增加 。
19．从某天起，池塘水面上的浮草，每天增加一倍，50天后整个池塘长满了浮草，第 天时，浮草所占面积是池塘的14。
20．经过旋转的图形与原来图形的 和 完全相同．
四、注意审题，用心计算。(每题6分，共18分）
21．直接写得数。
22．计算下面各题，能简算的要简算．
（1）（49+56-14）×72
（2）1.5×[ 0.02÷（2.1-2.09）]
（3）12÷[1-（13+715）]
（4）6.5×2.4+6.5×4.6+0.3×65
（5）（7.8-2.4）÷15×518
（6）45÷[(58-12)÷14]
23．解方程．
（1）34：725=57：x
（2）x+0.2x=920
（3）0.81x−144=0.69x
五、看清要求，动手操作。(每题6分，共12分）
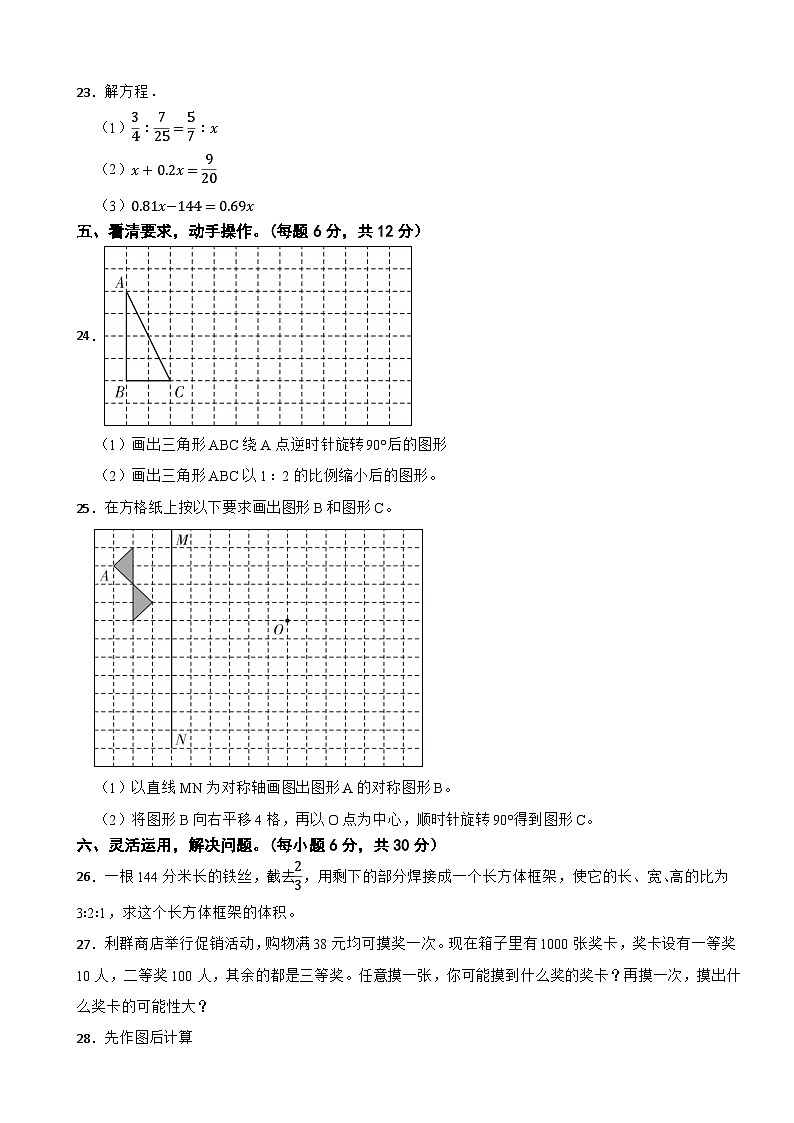
24．
（1）画出三角形ABC绕A点逆时针旋转90°后的图形
（2）画出三角形ABC以1：2的比例缩小后的图形。
25．在方格纸上按以下要求画出图形B和图形C。
（1）以直线MN为对称轴画图出图形A的对称图形B。
（2）将图形B向右平移4格，再以O点为中心，顺时针旋转90°得到图形C。
六、灵活运用，解决问题。(每小题6分，共30分）
26．一根144分米长的铁丝，截去23，用剩下的部分焊接成一个长方体框架，使它的长、宽、高的比为3∶2∶1，求这个长方体框架的体积。
27．利群商店举行促销活动，购物满38元均可摸奖一次。现在箱子里有1000张奖卡，奖卡设有一等奖10人，二等奖100人，其余的都是三等奖。任意摸一张，你可能摸到什么奖的奖卡？再摸一次，摸出什么奖卡的可能性大？
28．先作图后计算
（1）画圆．画一个直径为4厘米的圆．
（2）画正方形．在已画出的圆中画出一个最大的正方形．
（3）计算圆中最大的正方形的面积与圆的面积比．
29．已知正整数p和q都是质数，并且7p+q与pq+11也都是质数，求p和q的值。
30．一辆汽车从A地开往B地，前3小时匀速行驶了180千米，照这样的速度，还要行驶1.5小时才能到达B地。A、B两地相距多少千米？(用比例知识解答)
答案解析部分
1．【答案】错误
【知识点】统计图的选择
【解析】【解答】 表示一个星期的气温变化情况，选用折线统计图比较合适，原题说法错误。
故答案为：错误。
【分析】条形统计图特点：可以清楚地看出数量的多少；折线统计图特点：不但可以表示数量的多少，还可以清楚的看出数量的增减变化情况；扇形统计图特点：可以看出各个部分数量与总数之间的关系，据此结合题意选择合适的统计图。
2．【答案】错误
【知识点】除数是分数的分数除法
【解析】【解答】解：3÷23=3×32=92，原来计算错误。
故答案为：错误。
【分析】一个数除以一个不是0的数，等于乘这个数的倒数。先把除法转化成乘法再计算即可。
3．【答案】错误
【知识点】倒数的认识
【解析】【解答】解：1是它本身倒数的100％。原题说法错误。
故答案为：错误。
【分析】乘积是1的两个数互为倒数，1的倒数是1，也就是它本身倒数的100%。
4．【答案】错误
【知识点】比的化简与求值
【解析】【解答】解：从家到学校，甲用15分钟，乙用20分钟，甲乙的速度比是115：120=4：3。原题说法错误。
故答案为：错误。
【分析】把两地的距离看作单位“1”，用分数表示出两人的速度，写出速度的比并化成最简整数比即可。
5．【答案】错误
【知识点】百分数的应用--求百分率
【解析】【解答】2÷（50+2）×100%
≈0.038×100%
=3.8%
故答案为：错误
【分析】缺勤率=缺勤人数÷（出勤人数+缺勤人数）×100%。
6．【答案】C
【知识点】自然数的认识
【解析】【解答】解：90-3×3=81
故答案为：C。
【分析】相邻两个自然数的差是1。6个连续的自然数，前三个自然数都比相对应的后三个自然数分别少3，因此用90减去3个3就是前三个自然数的和。
7．【答案】B
【知识点】比例尺的认识
【解析】【解答】解：10厘米：5毫米=100毫米：5毫米=20：1。
故答案为：B。
【分析】图上距离：实际距离=比例尺，把图上距离换算成毫米，写出图上距离与实际距离的比并化成后项是1的比即可。
8．【答案】C
【知识点】比的化简与求值
【解析】【解答】解：假设圆锥和圆柱的高是h。
3×h×13：1×h=1：1。
故答案为：C。
【分析】假设圆锥和圆柱的高是h，圆锥的体积=底面积×高×13，圆柱的体积=底面积×高，写出比后化简比。
9．【答案】C
【知识点】圆柱的侧面积、表面积
【解析】【解答】解：半径：4÷2=2（厘米），
高：40÷2÷2=10（厘米）。
故答案为：C。
【分析】拼成的近似长方体比原来的表面积增加了左右两个长方形面的面积，每个长方形的面的长是圆柱的底面半径，宽就是圆柱的高。因此用每个长方形面的面积除以底面半径即可求出圆柱的高。
10．【答案】C
【知识点】分数与除法的关系；分数除法的应用
【解析】【解答】10÷（10+100）=111
故答案为：C
【分析】求一个数是另一个数的几分之几，用除法计算。盐水重量=盐的重量+水的重量。
11．【答案】3；2；40
【知识点】分数除法与分数加减法的混合运算；比的化简与求值
【解析】【解答】解：大长方形的面积：小长方形的面积=14：16=3：2；
4÷16＋4÷14
=24＋16
=40（平方厘米）。
故答案为：3；2；40。
【分析】依据大长方形的面积：小长方形的面积=14：16化简比求出最简比是3：2；整个图形的面积=阴影部分的面积÷阴影部分占大长方形的分率＋阴影部分的面积÷阴影部分占小长方形的分率。
12．【答案】（3+3÷7）×7
【知识点】含括号的运算顺序
【解析】【解答】解：算式：（3+3÷7）×7=24。
故答案为：（3+3÷7）×7（答案不唯一）。
【分析】使用四种运算符号，还可以使用括号来改变运算顺序。经过试算后确定算式即可。
13．【答案】三角形；三角形；一半
【知识点】平行四边形的切拼
【解析】【解答】解：两个完全一样的三角形可以拼成一个平行四边形，因此一个三角形的面积是所拼成的平行四边形没觉得一半。
故答案为：三角形；三角形；一半。
【分析】把两个完全相同的三角形的对应的边颠倒后重叠在一起即可拼出一个平行四边形，平行四边形面积就是两个三角形面积的和。
14．【答案】6
【知识点】最大公因数的应用
【解析】【解答】解：30=2×3×5，24=2×2×2×3，30和24的最大公因数是：2×3=6，所以正方形的边长最长是6厘米.
故答案为：6
【分析】分割成的正方形的边长一定是30和24的公因数，因为求最长的正方形边长，所以边长是这两个数的最大公因数.
15．【答案】4.71
【知识点】圆柱的体积（容积）；圆锥的体积（容积）
【解析】【解答】解：底面半径：18.84÷3.14÷2=3（米）；
装的高度：
3.14×32×1×13÷2
=3.14×3÷2
=4.71（米）
故答案为：4.71。
【分析】玉米的体积是不变的。用圆锥的底面周长除以3.14再除以2求出底面半径，用圆锥的底面积乘高再乘13求出玉米的体积，用玉米的体积除以圆柱形容器的底面积即可求出能装的高度。
16．【答案】32
【知识点】三角形的面积
【解析】【解答】解：40÷4=10（厘米）
10×10÷2-10×（10-6.4）÷2
=50-10×3.6÷2
=50-18
=32（平方厘米）
故答案为：32。
【分析】用三角形BCF的面积减去三角形BCE的面积就是阴影部分的面积。三角形BCF的底和高都是10厘米；三角形BCE的底是10厘米，高是（10-6.4）厘米。
17．【答案】7∶12；712
【知识点】比的化简与求值
【解析】【解答】解：把78∶1.5化成最简单的整数比是（78×8）：（1.5×8）=7：12，比值是7÷12=712。
故答案为：7：12；712。
【分析】根据比的基本性质，把比的前项和后项同时乘8即可化成最简单的整数比。用化简后比的前项除以后项即可求出比值。
18．【答案】120平方厘米
【知识点】圆柱的侧面积、表面积
【解析】【解答】解：12×5×2=120（平方厘米）
故答案为：120平方厘米。
【分析】把这个圆柱按照这样的方法切割后，表面积会增加两个长方形面的面积，长方形的一条边就是圆柱的底面直径，另一条边就是长方体的高。因此用底面直径乘高求出一个切割面的面积，再乘2就是表面积增加的部分。
19．【答案】48
【知识点】逆推问题
【解析】【解答】解：第49天时，浮草所占面积是池塘面积的12，那么第48天时，浮草所占的面积是池塘面积的14。
故答案为：48。
【分析】可以采用倒推的方法，先确定第49天浮草占的分率，然后推算第48天所占的分率。
20．【答案】形状；大小
【知识点】平移与平移现象
21．【答案】
【知识点】除数是分数的分数除法
【解析】【分析】异分母分数相加减，先通分再按照同分母分数加减法的计算方法计算；计算分数乘法时能约分的要先约分再乘；计算分数除法时要把除法转化成乘法再计算；估算减法时把两个数都看作整千数计算；估算小数除法时把两个数都看作整数计算；一个数的平方就是两个这样的数相乘。
22．【答案】（1）解：（49+56-14）×72
=49×72+56×72-14×72
=32+60-18
=74
（2）解：1.5×[ 0.02÷（2.1-2.09）]
=1.5×（0.02÷0.01）
=1.5×2
=3
（3）解：12÷[1-（13+715）]
=12÷（1-45）
=12×5
=212
（4）解：6.5×2.4+6.5×4.6+0.3×65
=6.5×2.4+6.5×4.6+3×6.5
=6.5×（2.4+4.6+3）
=6.5×10
=65
（5）解：（7.8-2.4）÷15×518
=5.4×5×518
=27×518
=712
（6）解：45÷[(58-12)÷14]
=45÷（18×4）
=45÷12
=135
【知识点】分数四则混合运算及应用；小数乘法运算律；分数乘法运算律
【解析】【分析】（1）运用乘法分配律简便计算；
（2）先算小括号里面的减法，再算中括号里面的除法，最后计算中括号外面的乘法；
（3）先算小括号里面的加法，再算中括号里面的减法，最后计算中括号外面的除法；
（4）把0.3×65变换成3×6.5，然后运用乘法分配律简便计算；
（5）先算小括号里面的减法，再算小括号外面的除法和乘法；
（6）先算小括号里面的减法，再算中括号里面的除法，最后计算中括号外面的除法。
23．【答案】（1） 34：725=57：x
解：34x=725×57
x=15÷34
x=415
（2）x+0.2x=920 解：1.2x=920
x=920÷65
x=38
（3） 0.81x−144=0.69x
解：0.81x-0.69x=144
0.12x=144
x=144÷0.12
x=1200
【知识点】综合应用等式的性质解方程；应用比例的基本性质解比例；列方程解关于分数问题
【解析】【分析】解方程要掌握等式的性质，即等式两边加上或减去同一个数，同时乘或除以一个不为0的数，等式仍然成立。解比例时根据比例的基本性质把比例写成两个内项积等于两个外项积的形式，然后根据等式的性质求出未知数的值。
24．【答案】（1）
（2）
【知识点】图形的缩放；作旋转后的图形
【解析】【分析】（1）先确定旋转中心，然后根据旋转方向和度数确定对应点的位置，再画出旋转后的图形；
（2）按1：2缩小后的三角形两条直角边的长度分别是2格和1格，由此画出这个三角形。
25．【答案】（1）
（2）
【知识点】补全轴对称图形；作旋转后的图形
【解析】【分析】（1）轴对称图形对应点到对称轴的距离相等，先确定对应点的位置，再画出轴对称图形；
（2）先确定向右平移4格后的图形位置，然后根据旋转中心、旋转方向和度数画出旋转后的图形。
26．【答案】解：144×(1−23)
=144×13
＝48(分米)
48÷4＝12(分米)
3＋2＋1＝6
长：12×36＝6(分米)
宽：12×26＝4(分米)
高：12×16＝2(分米)
6×4×2＝48(立方分米)
答：这个长方体框架的体积是48立方分米。
【知识点】比的应用
【解析】【分析】用铁丝的长度乘（1-23）求出剩下的长度，把剩下的长度按照3：2：1的比分配后分别求出长方体的长宽高，然后求出长方体的体积。
27．【答案】解：任意摸一张，可能摸出一等奖，也可能摸出二等奖，还可能摸出三等奖。再摸一次，摸出三等奖奖卡的可能性大。
【知识点】事件的确定性与不确定性
【解析】【分析】任意摸一张，每张奖卡都有被摸出的可能。再摸一次，哪种奖卡的数量多，摸出的可能性就大。
28．【答案】（1）解：根据分析画图如下：
（2）解：根据分析画图如下：
（3）解：正方形的面积为：4×（4÷2）÷2×2
=4×2÷2×2
=8（平方厘米），
圆的面积为：3.14×（4÷2）2
=3.14×4
=12.56（平方厘米），
正方形的面积：圆的面积=8：12.56=100：157；
答：正方形的面积与圆的面积比是100：157
【知识点】圆与组合图形；比的应用
【解析】【分析】（1）圆心确定圆的位置，半径确定圆的大小，由此以任意一点O为圆心，以4÷2=2厘米为半径画圆即可；（2）圆内最大的正方形的对角线即为圆的直径，先画出两条互相垂直的直径，再连接直径与圆的交点，即为圆里最大的正方形；（3）因为这个最大正方形的对角线等于圆的直径，所以利用正方形和圆的面积公式即可求出正方形和圆的面积比．
29．【答案】解：因为pq+11是质数，11是质数，所以pq一定是偶数。因为p、q都是质数，所以p、q一定有一个数是2。
当p=2时，7p+q=14+q，pq+11=2q+11，此时q=3；
当p=3时，7p+q=21+q，pq+11=3q+11，此时p=2。
答：p和q的值为2，3或3，2
【知识点】合数与质数的特征
【解析】【分析】质数是只有1和本身两个因数的数，2是所有质数中唯一的偶数，其余的质数都是奇数。然后根据奇数与偶数的特征初步判断p、q有一个数一定是2。然后根据质数的特征确定另外一个字母表示的数。
30．【答案】解：设A、B两地相距x千米。
180：3=x：（3+1.5）
3x=180×4.5
x=810÷3
x=270
答：A、B两地相距270千米。
【知识点】正比例应用题
【解析】【分析】速度不变，路程与时间的比值相等，那么路程与时间成正比例关系。设两地的距离是x千米，根据路程与时间的比值相等列出比例解答即可。12−14＝
38×83＝
10001－999≈
15÷25＝
(13)2＝
20.97÷3.01≈
12−14＝14
38×83＝1
10001－999≈9000
15÷25＝12
(13)2＝19
20.97÷3.01≈7