所属成套资源：2024年高考数学必备PPT大全（6大专题秘籍大招）

成套系列资料，整套一键下载

浏览整套资料 (共50份)

专题一　第2讲　基本初等函数、函数与方程--高三高考数学复习-PPT

展开

这是一份专题一　第2讲　基本初等函数、函数与方程--高三高考数学复习-PPT，共60页。PPT课件主要包含了考点一，考点二，考点三，函数的零点，函数模型及其应用，专题强化练，核心提炼，1＋∞，故至少需要过滤5次，所以C错误D正确等内容，欢迎下载使用。

1.基本初等函数的图象与性质是高考考查的重点，利用函数性质比较大小、解不等式是常见题型.2.函数零点的个数判断及参数范围是常考题型，常以压轴题的形式出现.3.函数模型及应用是近几年高考的热点，通常考查指数函数、对数函数模型.
基本初等函数的图象与性质
指数函数y＝ax(a>0，且a≠1)与对数函数y＝lgax(a>0，且a≠1)互为反函数，其图象关于y＝x对称，它们的图象和性质分01两种情况，着重关注两种函数图象的异同.
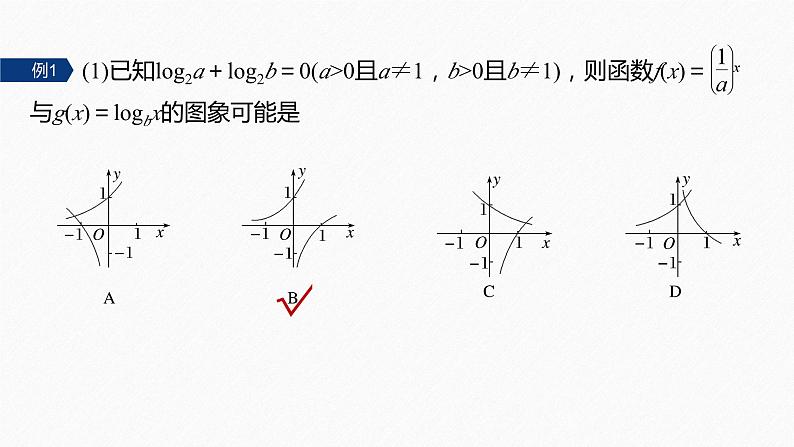
　(1)已知lg2a＋lg2b＝0(a>0且a≠1，b>0且b≠1)，则函数f(x)＝与g(x)＝lgbx的图象可能是
lg2a＋lg2b＝0，即为lg2ab＝0，即有ab＝1，当a＞1时，0＜b＜1，
当0＜a＜1时，b＞1，
(2)(2023·六盘水质检)设a＝0.70.8，b＝0.80.7，c＝lg0.80.7，则a，b，c的大小关系为A.b>c>a B.a>c>bC.c>a>b D.c>b>a
由对数函数的性质，可得c＝lg0.80.7>lg0.80.8＝1，又由指数函数的性质，可得1>b＝0.80.7>0.80.8，由幂函数y＝x0.8在(0，＋∞)上单调递增，可得0.80.8>0.70.8＝a，所以1>b>a，所以lg0.80.7>0.80.7>0.70.8，即c>b>a.
(1)指数函数、对数函数的图象与性质受底数a的影响，解决与指数函数、对数函数有关的问题时，首先要看底数a的取值范围.(2)基本初等函数的图象和性质是统一的，在解题中可相互转化.
　　　(1)(多选)(2023·惠州模拟)若6a＝2,6b＝3，则
因为6b＝3,6a＝2，所以b＝lg63，a＝lg62，则a＋b＝lg66＝1，故A正确；
选项C，因为a>0，b>0，a≠b，
(2)(2023·邯郸模拟)不等式10x－6x－3x≥1的解集为___________.
由10x－6x－3x≥1，
故不等式10x－6x－3x≥1的解集为[1，＋∞).
判断函数零点个数的方法(1)利用函数零点存在定理判断.(2)代数法：求方程f(x)＝0的实数根.(3)几何法：对于不易求根的方程，将它与函数y＝f(x)的图象联系起来，利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时，可用求导的方法判断函数的单调性.
考向1　函数零点个数的判断
所以f(x)＝－sin 2x，
考向2　求参数的值或范围
　若关于x的方程ex＝a|x|恰有两个不同的实数解，则实数a＝___.
如图，显然a>0.当x≤0时，由单调性得方程ex＝－ax有且仅有一解.因此当x>0时，方程ex＝ax只有一解.即y＝ax与y＝ex相切，y′＝ex，令y′＝a得x＝ln a，故当x＝ln a时，ex＝ax，得eln a＝aln a，即a＝aln a，从而a＝e，故当a＝e时，y＝ax与函数y＝ex相切，此时方程ex＝ax有一解，若方程ex＝a|x|恰有两个不同的解，则a＝e.
利用函数零点的情况求参数值(或取值范围)的三种方法
　(1)函数f(x)＝　　　　　　　　的零点个数为A.1 　　　B.2 　　　 C.3　　　 D.4
当x≥0时，f(x)＝2x＋3x－4在(0，＋∞)上单调递增且f(0)f(1)<0，∴f(x)在(0,1)上有唯一零点；当x<0时，令x2＋2x＝0，解得x＝－2(舍x＝0)，故f(x)共有2个零点.
(2)(2023·九江模拟)函数f(x)＝　　　－|x－1|的所有零点之和为____.
对称轴为x＝1＋2k，k∈Z，且h(x)的对称轴为x＝1，
因为g(x)与h(x)有6个交点，所以f(x)在[－3,5]上存在6个零点，因为g(x)和h(x)的函数图象关于x＝1对称，则f(x)零点关于x＝1对称，所以f(x)的所有零点之和为6×1＝6.
解函数应用题的步骤(1)审题：缜密审题，准确理解题意，分清条件和结论，理清数量关系.(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型.(3)求模：求解数学模型，得出数学结论.(4)反馈：将得到的数学结论还原为实际问题的意义.
　(1)某纯净水制造厂在净化水的过程中，每增加一次过滤可使水中杂质减少50%，若要使水中杂质减少到原来的5%以下，则至少需要过滤(参考数据：lg 2≈0.301 0)A.2次 B.3次C.4次 D.5次
设经过n(n∈N*)次过滤后，水中杂质减少到原来的5%以下，则(1－50%)n<5%，
不等式两边取常用对数得nlg 2>lg 2＋1，
(2)(多选)(2023·新高考全国Ⅰ)噪声污染问题越来越受到重视.用声压级来度量声音的强弱，定义声压级Lp＝20× 　，其中常数p0(p0>0)是听觉下限阈值，p是实际声压.下表为不同声源的声压级：
已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为p1，p2，p3，则A.p1≥p2 B.p2>10p3C.p3＝100p0 D.p1≤100p2
所以　　　，所以p1≥p2，故A正确；
所以p1≤100p2，故D正确.
构建函数模型解决实际问题的失分点(1)不能选择相应变量得到函数模型.(2)构建的函数模型有误.(3)忽视函数模型中变量的实际意义.
　(1)(2023·合肥模拟)Malthus模型是一种重要的数学模型.某研究人员在研究一种细菌繁殖数量N(t)与时间t的关系时，得到的Malthus模型是N(t)＝N0e0.46t，其中N0是t＝t0时刻的细菌数量，e为自然对数的底数.若t时刻细菌数量是t0时刻细菌数量的6.3倍，则t约为(ln 6.3≈1.84)A.2 B.3C.4 D.5
由题意得，N(t)＝N0e0.46t＝6.3N0，即e0.46t＝6.3，则0.46t＝ln 6.3≈1.84，得t≈4.
(2)金针菇采摘后会很快失去新鲜度，甚至腐烂，所以超市销售金针菇时需要采取保鲜膜封闭保存.已知金针菇失去的新鲜度h与其采摘后时间t(天)满足的函数解析式为h＝mln(t＋a)(a>0).若采摘后1天，金针菇失去的新鲜度为40%，采摘后3天，金针菇失去的新鲜度为80%.那么若不及时处理，采摘下来的金针菇在多长时间后开始失去全部新鲜度(已知　 ≈1.414，结果取一位小数)A.4.0天 B.4.3天C.4.7天 D.5.1天
ln(3＋a)＝2ln(1＋a)，(1＋a)2＝3＋a，因为a>0，故解得a＝1，设t天后开始失去全部新鲜度，则mln(t＋1)＝1，又mln(1＋1)＝0.4，
2ln(t＋1)＝5ln 2＝ln 32，
一、单项选择题1.已知幂函数y＝f(x)的图象过点(8,　 )，则f(9)的值为A.2 B.3C.4 D.9
2.(2023·南昌模拟)已知a＝lg40.4，b＝lg0.40.2，c＝0.40.2，则A.c>a>b B.c>b>aC.b>c>a D.a>c>b
因为a＝lg40.4lg0.40.4＝1，0c>a.
因为2a＝9，所以a＝lg29＝lg232＝2lg23，
4.已知函数y＝lga(x＋c)(a，c为常数，其中a>0，a≠1)的图象如图所示，则下列结论成立的是A.a>1，c>1B.a>1,01D.0由题图可知函数为减函数，结合y＝lga(x＋c)可知01，∴c>0，当x＝0时，lgac>0，∴05.(2023·银川模拟)函数f(x)＝lg2x＋x2＋m在区间(2,4)上存在零点，则实数m的取值范围是A.(－∞，－18) B.(5，＋∞)C.(5,18) D.(－18，－5)
由函数零点存在定理可知，若函数f(x)＝lg2x＋x2＋m在区间(2,4)上存在零点，显然函数为增函数，只需满足f(2)·f(4)<0，即(m＋5)(m＋18)<0，解得－18A.a>b>c B.b>a>cC.c>b>a D.a>c>b
7.(2023·郑州模拟)某中学坚持“五育”并举，全面推进素质教育.为了更好地增强学生们的身体素质，校长带领同学们一起做俯卧撑锻炼.锻炼是否达到中等强度运动，简单测量方法为f(t)＝ket，其中t为运动后心率(单位：次/分)与正常时心率的比值，k为每个个体的体质健康系数.若f(t)介于[28,34]之间，则达到了中等强度运动；若低于28，则运动不足；若高于34，则运动过量.已知某同学正常时心率为80，体质健康系数k＝7，经过俯卧撑后心率y(单位：次/分)满足y＝　　　　　　，x为俯卧撑个数.已知俯卧撑每组12个，若该同学要达到中等强度运动，则较合适的俯卧撑组数为(e为自然对数的底数，e≈2.718)A.2 　　　B.3 　　　 C.4　　　 D.5
由题意，设俯卧撑组数为a(a∈N*)，则x＝12a，
8.(2023·铜陵模拟)已知a＝lg75，b＝lg97，c＝lg119，则A.a所以lg75－lg97<0，即a所以lg97－lg119<0，即b二、多项选择题9.(2023·红河模拟)下列函数中，是奇函数且存在零点的是
对于B，设f(x)＝x3＋x，x∈R，则f(－x)＝(－x)3－x＝－x3－x＝－f(x)，得y＝x3＋x为奇函数，令x3＋x＝0，得x＝0，即函数存在零点，B符合；
当a>b>0时，A正确；当2a>b>a>0时，B正确；当0>a>b>2a时，D正确；
设2a＝3b＝6c＝t，
因为f(x)的定义域为R，
所以f(－x)＝lg4(2x＋2－x)＝f(x)，所以f(x)为偶函数，所以A错误，B正确；
又t＝2x为增函数，所以f(x)在[0，＋∞)上单调递增.又f(x)为R上的偶函数，
三、填空题13.(2023·深圳模拟)若函数f(x)＝－　的零点属于区间(n，n＋1)(n∈N)，则n＝_____.
所以函数在(0,1)上有唯一零点，所以n＝0.
函数y＝4[f(x)]2－8f(x)＋3的零点即为方程4[f(x)]2－8f(x)＋3＝0的根，
作出函数y＝f(x)的图象，如图所示.
因此函数y＝4[f(x)]2－8f(x)＋3的零点有7个.
15.(2023·聊城模拟)“环境就是民生，青山就是美丽，蓝天也是幸福”，随着经济的发展和社会的进步，人们的环保意识日益增强.某化工厂产生的废气中污染物的含量为1.2 mg/cm3，排放前每过滤一次，该污染物的含量都会减少20%，当地环保部门要求废气中该污染物的含量不能超过0.2 mg/cm3，若要使该工厂的废气达标排放，那么该污染物排放前需要过滤的次数至少为____.(参考数据：lg 2≈0.3，lg 3≈0.477)
设该污染物排放前过滤的次数为n(n∈N*)，
因为lg 2≈0.3，lg 3≈0.477，
所以n≥7.77，又n∈N*，所以nmin＝8，即该污染物排放前需要过滤的次数至少为8.
16.已知a>0且a≠1，方程xa＝ln x(x>0)有且仅有两个不相等的实数根，则a的取值范围为________.
由xa＝ln x(x>0)，得ln(ln x)＝aln x(x>1).
令g′(t)＝0，得t＝e.在(0，e)上g′(t)>0，g(t)单调递增；
在(e，＋∞)上g′(t)<0，g(t)单调递减，
又当t>1时，g(t)>0恒成立，所以方程xa＝ln x(x>0)有且仅有两个不相等的实数根，