

- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 2.1 不等式的性质及一元二次不等式(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 2.2 基本不等式(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 2.2 基本不等式(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.1 三角函数的定义(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.2 同角三角函数(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
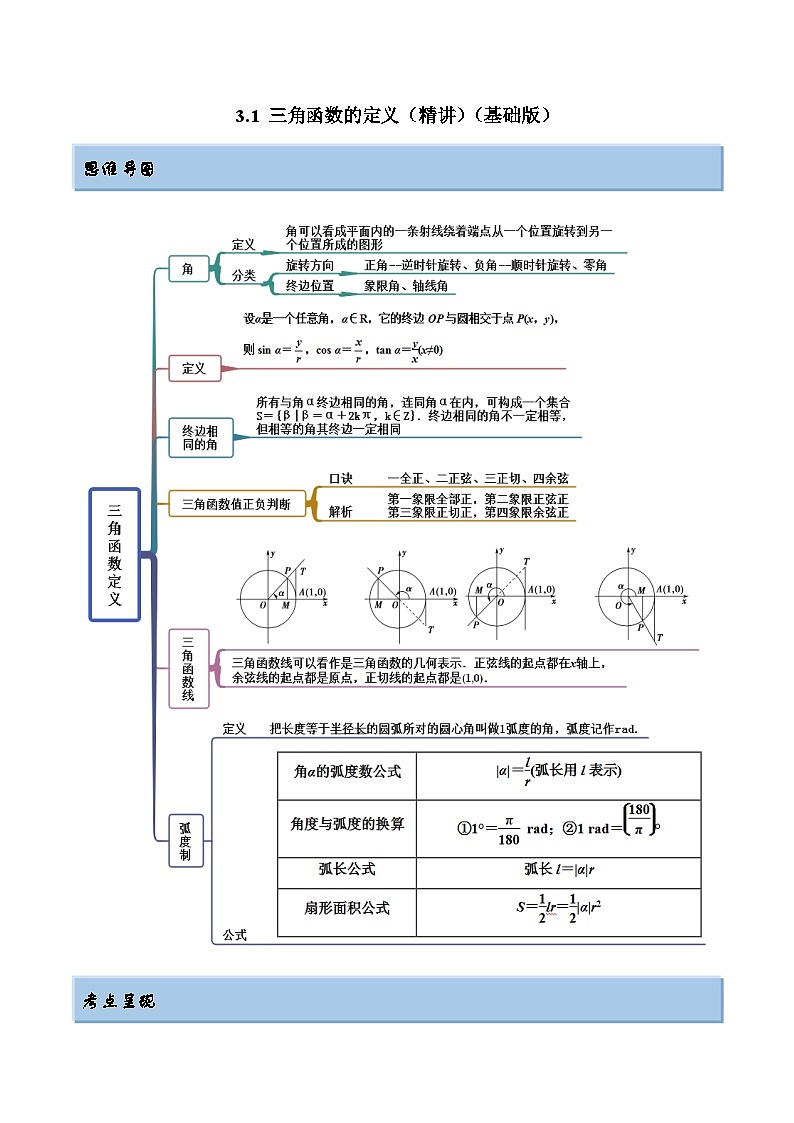
2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.1 三角函数的定义(精讲)(基础版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 扇形的弧长与面积
【例1-1】 (2023·安徽黄山市)若一扇形的圆心角为144°,半径为cm,则扇形的面积为______cm2.
【例1-2】 (2023·全国·贵阳一中二模)已知圆锥的母线长为3,其侧面展开图是一个圆心角为的扇形,则该圆锥的底面半径为___________.
【例1-3】 (2023·全国·高三专题练习)中国传统扇文化有着深厚的底蕴,一般情况下,折扇可以看做是从一个圆形中前下的扇形制作而成的,当折扇所在扇形的弧长与折扇所在扇形的周长的比值为时,折扇的外观看上去是比较美观的,则此时折扇所在扇形的圆心角的弧度数为( )
A.B.C.D.
【一隅三反】
1. (2023·浙江浙江·二模)《九章算术》是我国古代内容极为丰富的数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步.问为田几何?”其意思为:“有一块扇形的田,弧长为30步,其所在圆的直径为16步,问这块田的面积是多少平方步?”该问题的答案为___________平方步.
2. (2023·全国·高三专题练习)已知扇形的周长是6,面积是2,则扇形的圆心角的弧度数α是( )
A.1B.4C.1或4D.2或4
3. (2023·全国·高三专题练习)如图所示,扇环的两条弧长分别是4和10,两条直边与的长都是3,则此扇环的面积为( )
A.84B.63C.42D.21
4. (2023·全国·高三专题练习)《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为米,肩宽约为米,“弓”所在圆的半径约为1.25米,则掷铁饼者双手之间的距离约为( )
A.1.012米B.1.768米C.2.043米D.2.945米
考点二 三角函数的定义
【例2-1】 (2023·江西·芦溪中学)已知点是角终边上的一点,则( )
A.B.C.D.
【例2-2】 (2023·安徽)在平面直角坐标系中,若角的终边经过点,则( )
A.B.C.D.
【例2-3】 (2023·湖南·长沙一中高三阶段练习)若角的终边过点P(8m,),且,则m的值为( )
A.B.C.D.
【例2-4】 (2023·北京四中高三阶段练习)角的终边过点,则( )
A.B.C.D.
【一隅三反】
1. (2023·四川成都)如图,角以为始边,它的终边与圆相交于点,点的坐标为,则( )
A.B.C.D.
2. (2023·安徽)已知角的终边上有一点,则( )
A.B.C.D.
3. (2023·河南新乡·二模(理))已知点A是的终边与单位圆的交点,若A的横坐标为,则( )
A.B.C.D.
4. (2023·重庆巴蜀中学)已知角的终边过点,且,则的值为( )
A.B.C.D.
5. (2023·河南洛阳)已知角的顶点在原点,始边与x轴的非负半轴重合,终边经过点,则( ).
A.B.C.D.
考点三 象限的判断
【例3-1】 (2023·重庆·高三开学考试)若,则下列三角函数值为正值的是( )
A.B.C.D.
【例3-2】 (2023·全国·高三专题练习)若α是第四象限角,则π-α是第( )象限角.
A.一B.二C.三D.四
【例3-3】 (2023·浙江·高三专题练习)已知是第三象限角,满足,则是( )
A.第一象限B.第二象限
C.第三象限D.第四象限
【一隅三反】
1. (2023·山东枣庄·高三期末)为第三或第四象限角的充要条件是( ).
A.B.C.D.
2. (2023·甘肃酒泉·高三期中)若角满足,,则角所在的象限是( ).
A.第一象限B.第二象限C.第三象限D.第四象限
3. (2023·全国·高三专题练习(理))角的终边属于第一象限,那么的终边不可能属于的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
4. (2023·昆明市)若,则是( )
A.第一象限角B.第二象限角
C.第三象限角D.第四象限角
5. (2023·湖南高三月考)已知,,则是( )
A.第一象限角B.第二象限角C.第三象限角D.第四象限角
考点四 三角函数线
【例4-1】 (2023·全国·高三专题练习)已知,且,则的取值范围是( ).
A.B. C.D.
【例4-2】 (2023·全国·高三专题练习)若-<α<-,从单位圆中的三角函数线观察sin α,cs α,tan α的大小是( )
A.sin α<tan α<cs αB.cs α<sin α<tan α
C.sin α<cs α<tan αD.tan α<sin α<cs α
【例4-3】 (2023·河南·南阳市第二完全学校高级中学高一阶段练习)已知,则的大小关系是( )
A.B.
C.D.
【一隅三反】
1. (2023·安徽·合肥市庐阳高级中学高三阶段练习(理))设,使且同时成立的取值范围是( )
A.B.C.D.
2. (2023·全国·高三专题练习)已知,,,则
A.B.C.D.
3 (2023·全国高三专题练习)已知点在第一象限,则在内的的取值范围是( )
A.B.
C.D.
3.1 三角函数的定义(精讲)(基础版)
思维导图
考点呈现
例题剖析
考点一 扇形的弧长与面积
【例1-1】 (2023·安徽黄山市)若一扇形的圆心角为144°,半径为cm,则扇形的面积为______cm2.
【答案】.
【解析】扇形的圆心角为144°,半径为,所以扇形的面积为.
故答案为:.
【例1-2】 (2023·全国·贵阳一中二模)已知圆锥的母线长为3,其侧面展开图是一个圆心角为的扇形,则该圆锥的底面半径为___________.
【答案】
【解析】因为圆锥的母线长为3,所以侧面展开图扇形的半径为3,设该圆锥的底面半径为,
所以有,故答案为:
【例1-3】 (2023·全国·高三专题练习)中国传统扇文化有着深厚的底蕴,一般情况下,折扇可以看做是从一个圆形中前下的扇形制作而成的,当折扇所在扇形的弧长与折扇所在扇形的周长的比值为时,折扇的外观看上去是比较美观的,则此时折扇所在扇形的圆心角的弧度数为( )
A.B.C.D.
【答案】A
【解析】设扇形的弧长为,半径为,圆心角的弧度数为,由题意得,变形可得,因为,所以折扇所在扇形的圆心角的弧度数为.故选:A.
【一隅三反】
1. (2023·浙江浙江·二模)《九章算术》是我国古代内容极为丰富的数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步.问为田几何?”其意思为:“有一块扇形的田,弧长为30步,其所在圆的直径为16步,问这块田的面积是多少平方步?”该问题的答案为___________平方步.
【答案】120
【解析】由题意得:扇形的弧长为30,半径为8,所以扇形的面积为:,
故答案为:120
2. (2023·全国·高三专题练习)已知扇形的周长是6,面积是2,则扇形的圆心角的弧度数α是( )
A.1B.4C.1或4D.2或4
【答案】C
【解析】设扇形所在圆的半径为,由扇形的周长是6,面积是2,可得,解得或,
又由弧长公式,可得,即,当时,可得;当时,可得,
故选:C.
3. (2023·全国·高三专题练习)如图所示,扇环的两条弧长分别是4和10,两条直边与的长都是3,则此扇环的面积为( )
A.84B.63C.42D.21
【答案】D
【解析】设扇环的圆心角为,小圆弧的半径为,由题可得且,解得,,从而扇环面积.故选:D.
4. (2023·全国·高三专题练习)《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为米,肩宽约为米,“弓”所在圆的半径约为1.25米,则掷铁饼者双手之间的距离约为( )
A.1.012米B.1.768米C.2.043米D.2.945米
【答案】B
【解析】由题得:弓所在的弧长为:;
所以其所对的圆心角;
两手之间的距离.故选:B.
考点二 三角函数的定义
【例2-1】 (2023·江西·芦溪中学)已知点是角终边上的一点,则( )
A.B.C.D.
【答案】D
【解析】因点是角终边上的一点,则,所以.故选:D
【例2-2】 (2023·安徽)在平面直角坐标系中,若角的终边经过点,则( )
A.B.C.D.
【答案】D
【解析】由角的终边经过点,即,所以.故选:D.
【例2-3】 (2023·湖南·长沙一中高三阶段练习)若角的终边过点P(8m,),且,则m的值为( )
A.B.C.D.
【答案】A
【解析】∵,∴,故选:A.
【例2-4】 (2023·北京四中高三阶段练习)角的终边过点,则( )
A.B.C.D.
【答案】B
【解析】角的终边过点,,.故选:B.
【一隅三反】
1. (2023·四川成都)如图,角以为始边,它的终边与圆相交于点,点的坐标为,则( )
A.B.C.D.
【答案】A
【解析】根据三角函数定义,.故选:A
2. (2023·安徽)已知角的终边上有一点,则( )
A.B.C.D.
【答案】B
【解析】依题意,.故选:B
3. (2023·河南新乡·二模(理))已知点A是的终边与单位圆的交点,若A的横坐标为,则( )
A.B.C.D.
【答案】C
【解析】由题意知,,所以.故选:C
4. (2023·重庆巴蜀中学)已知角的终边过点,且,则的值为( )
A.B.C.D.
【答案】B
【解析】因为角的终边过点,且,故可得,解得,则.故选:B.
5. (2023·河南洛阳)已知角的顶点在原点,始边与x轴的非负半轴重合,终边经过点,则( ).
A.B.C.D.
【答案】C
【解析】由正切函数的定义得
.故选:C
考点三 象限的判断
【例3-1】 (2023·重庆·高三开学考试)若,则下列三角函数值为正值的是( )
A.B.C.D.
【答案】C
【解析】,所以C选项正确.
当时,,所以ABD选项错误.故选:C
【例3-2】 (2023·全国·高三专题练习)若α是第四象限角,则π-α是第( )象限角.
A.一B.二C.三D.四
【答案】C
【解析】∵α是第四象限角,∴-+2kπ<α<2kπ,k∈Z,∴-2kπ<-α<-2kπ+,k∈Z,
∴π-2kπ<π-α<-2kπ+π,k∈Z,故π-α是第三象限角.故选:C
【例3-3】 (2023·浙江·高三专题练习)已知是第三象限角,满足,则是( )
A.第一象限B.第二象限
C.第三象限D.第四象限
【答案】D
【解析】是第三象限角,,,则,,即为第二或第四象限角,又,为第四象限角.故选:D.
【一隅三反】
1. (2023·山东枣庄·高三期末)为第三或第四象限角的充要条件是( ).
A.B.C.D.
【答案】D
【解析】对于A:第三或第四象限角,以及终边在y轴负半轴,故A错误;
对于B:第二或第三象限角,以及终边在x轴负半轴,故B错误;
对于C:第二或第三象限角,故C错误;
对于D:第三或第四象限角,故D正确.故选:D
2. (2023·甘肃酒泉·高三期中)若角满足,,则角所在的象限是( ).
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】C
【解析】由知,是一、三象限角,由知,是三、四象限角或终边在y轴负半轴上,
故是第三象限角.故选:C
3. (2023·全国·高三专题练习(理))角的终边属于第一象限,那么的终边不可能属于的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
【答案】D
【解析】∵角的终边在第一象限,
∴,,则,,
当时,此时的终边落在第一象限,
当时,此时的终边落在第二象限,
当时,此时的终边落在第三象限,
综上,角的终边不可能落在第四象限,
故选:D.
4. (2023·昆明市)若,则是( )
A.第一象限角B.第二象限角
C.第三象限角D.第四象限角
【答案】B
【解析】因为,又,所以,所以是第二象限角.故选:B
5. (2023·湖南高三月考)已知,,则是( )
A.第一象限角B.第二象限角C.第三象限角D.第四象限角
【答案】B
【解析】由得,则,
又,所以是第二象限角.故选:B.
考点四 三角函数线
【例4-1】 (2023·全国·高三专题练习)已知,且,则的取值范围是( ).
A.B.C.D.
【答案】D
【解析】画出单位圆以及,,,
∵,且,
从图中可知的取值范围是
故选:D.
【例4-2】 (2023·全国·高三专题练习)若-<α<-,从单位圆中的三角函数线观察sin α,cs α,tan α的大小是( )
A.sin α<tan α<cs αB.cs α<sin α<tan α
C.sin α<cs α<tan αD.tan α<sin α<cs α
【答案】C
【解析】如图所示
作出角α的正弦线MP,余弦线OM,正切线AT,因为-<α<-,所以OM,MP均为负值,且,AT为正值,,故有sin α<cs α<tan α.
故选:C
【例4-3】 (2023·河南·南阳市第二完全学校高级中学高一阶段练习)已知,则的大小关系是( )
A.B.
C.D.
【答案】C
【解析】先证明:当0<x<时,
如图,角x终边为OP,其中点P为角x的终边与单位圆的交点,PM⊥x轴,交x轴与点M,
A点为单位圆与x轴的正半轴的交点,AT⊥x轴,交角x终边于点T,
则有向线段MP为角x的正弦线,有向线段AT为角x的正切线,设弧PA=l=x×1=x,
由图形可知:S△OAP<S扇形OAP<S△OAT,
即
所以<<,即
所以
又由函数在上单调递增,所以
又由函数在上单调递减,则
所以
所以,即
故选:C.
【一隅三反】
1. (2023·安徽·合肥市庐阳高级中学高三阶段练习(理))设,使且同时成立的取值范围是( )
A.B.C.D.
【答案】D
【解析】因为,由正弦曲线得:时,
由余弦曲线得:时,,
因为,所以且同时成立的x的取值范围是
故选:D
2. (2023·全国·高三专题练习)已知,,,则
A.B.C.D.
【答案】C
【解析】因为在上单调递增,,所以,而,,故选C.
3 (2023·全国高三专题练习)已知点在第一象限,则在内的的取值范围是( )
A.B.
C.D.
【答案】B
【解析】由已知点在第一象限得:
,,即,,
当,可得,.
当,可得或,.
或,.
当时,或.
,或.故选:B.
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.1 空间几何中的平行(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.1 空间几何中的平行(精讲)(基础版)(原卷版+解析版),共27页。试卷主要包含了三角形中位线,构造平行四边形,等比例,线面平行的性质,面面平行的性质,线面垂直的性质等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.3 统计案例(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.3 统计案例(精讲)(基础版)(原卷版+解析版),共33页。试卷主要包含了线性回归方程,非线性回归方程,独立性检验等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版),共25页。试卷主要包含了裂项相消,错位相减,分组求和,倒序相加等内容,欢迎下载使用。












