- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.7 空间几何的外接球(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.7 空间几何的外接球(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精讲)(基础版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 点线距
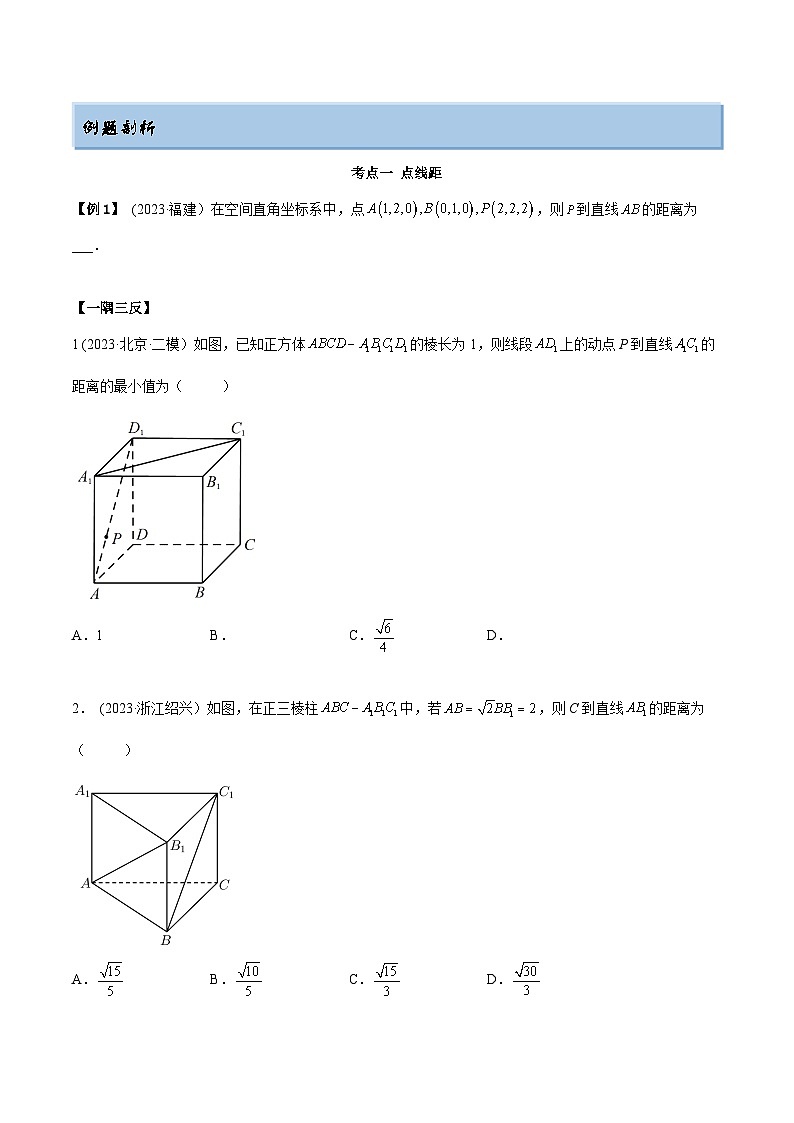
【例1】 (2023·福建)在空间直角坐标系中,点,则到直线的距离为___.
【一隅三反】
1 (2023·北京·二模)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1B.C.D.
2. (2023·浙江绍兴)如图,在正三棱柱中,若,则C到直线的距离为( )
A.B.C.D.
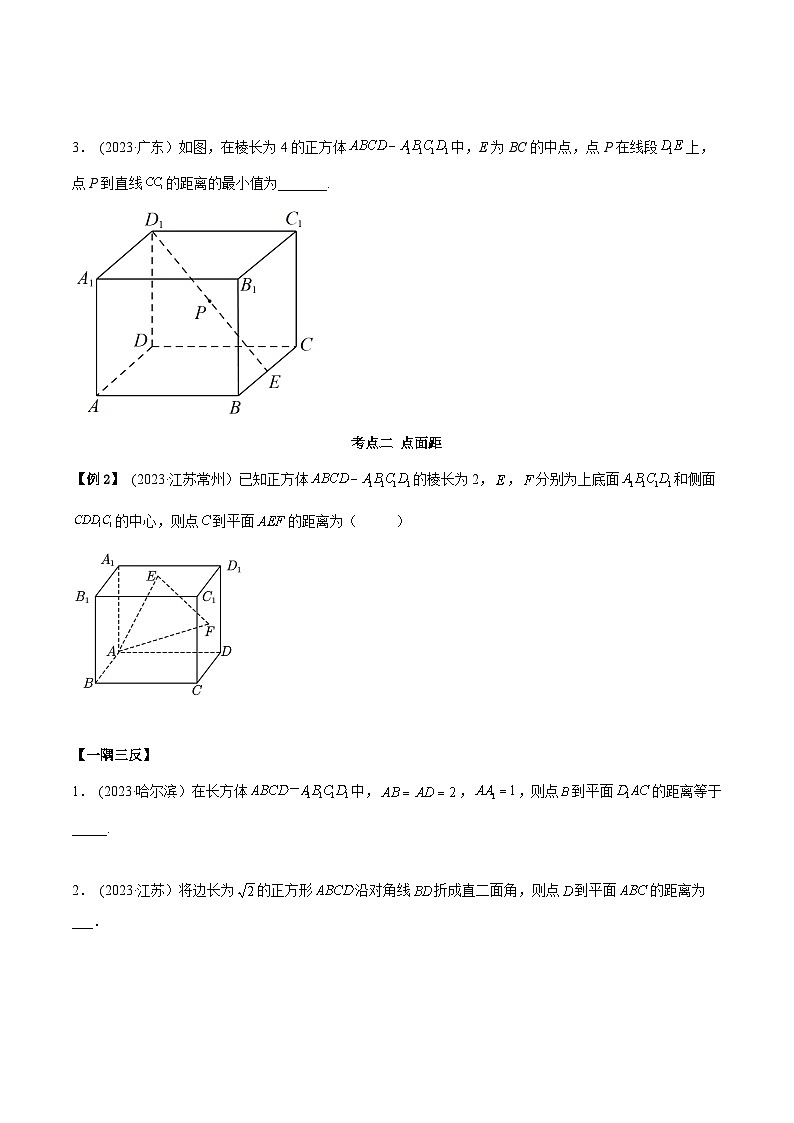
3. (2023·广东)如图,在棱长为4的正方体中,E为BC的中点,点P在线段上,点Р到直线的距离的最小值为_______.
考点二 点面距
【例2】 (2023·江苏常州)已知正方体的棱长为2,,分别为上底面和侧面的中心,则点到平面的距离为( )
【一隅三反】
1. (2023·哈尔滨)在长方体中,,,则点到平面的距离等于_____.
2. (2023·江苏)将边长为的正方形沿对角线折成直二面角,则点到平面的距离为___.
3. (2023·福建福州)如图,在正四棱柱中,已知,,E,F分别为,上的点,且.
(1)求证:平面ACF:
(2)求点B到平面ACF的距离.
考点三 线线距
【例3】 (2023·全国·高三专题练习)在长方体中,,,,则异面直线与之间的距离是( )
A.B.C.D.
【一隅三反】
1. (2023·山东)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体中,,,,则异面直线与之间的距离是( )
A.B.C.D.
2. (2023·江苏)长方体中,,,为的中点,则异面直线与之间的距离是( )
A.B.C.D.
3. (2023·全国·高三专题练习)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为1的正方体中,直线与之间的距离是( )
A.B.C.D.
考点四 线面距
【例4】 (2023广西)如图,已知斜三棱柱在底面上的射影恰为的中点又知.
(1)求证:平面;
(2)求到平面的距离.
【一隅三反】
1. (2023·山西)如图,在正方体中,为的中点.
(1)证明:平面AD1E
(2)求直线到平面的距离;
2. (2023·海南)如图,在正方体中,棱长为2,为的中点.
(1)求到平面的距离.
(2)若面,求.
3. (2023·北京)图1是直角梯形,四边形是边长为2的菱形,并且,以为折痕将折起,使点到达的位置,且,如图2.
(1)求证:平面平面;
(2)在棱上是否存在点,使得到平面的距离为?若存在,求出直线与平面所成角的正弦值.
考点五 面面距
【例5】 (2023·全国·高三专题练习)已知正方体的棱长为a,则平面与平面的距离为( )
A.B.C.D.
【一隅三反】
1. (2023·全国·高三专题练习)在棱长为的正方体中,则平面与平面之间的距离为
A.B.
C.D.
2.(2022山西)两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是 ( )
A.B.C.D.
3.(2022·青海西宁)底面为菱形的直棱柱中,分别为棱的中点.
(1)在图中作一个平面,使得,且平面.(不必给出证明过程,只要求作出与直棱柱的截面).
(2)若,求平面与平面的距离.
7.6 空间向量求空间距离(精讲)(基础版)
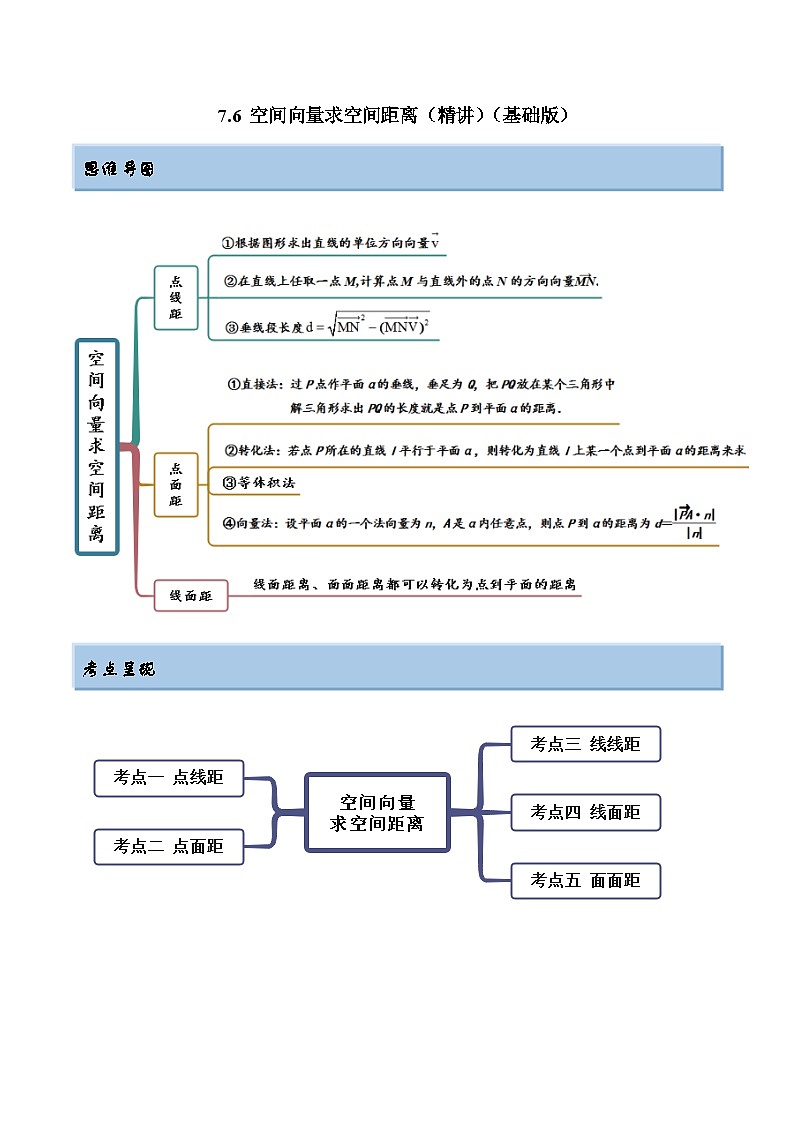
思维导图
考点呈现
例题剖析
考点一 点线距
【例1】 (2023·福建)在空间直角坐标系中,点,则到直线的距离为___.
【答案】
【解析】依题意得,则到直线的距离为故答案为:
【一隅三反】
1 (2023·北京·二模)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1B.C.D.
【答案】D
【解析】如图建立空间直角坐标系,则,
设,则,
∴动点P到直线的距离为
,当时取等号,
即线段上的动点P到直线的距离的最小值为.
故选:D.
2. (2023·浙江绍兴)如图,在正三棱柱中,若,则C到直线的距离为( )
A.B.C.D.
【答案】D
【解析】由题意知,,
取AC的中点O,则,
建立如图所示的空间直角坐标系,
则,
所以,
所以在上的投影的长度为,
故点C到直线的距离为:.
故选:D
3. (2023·广东)如图,在棱长为4的正方体中,E为BC的中点,点P在线段上,点Р到直线的距离的最小值为_______.
【答案】
【解析】在正方体中,建立如图所示的空间直角坐标系,
则,,
因点P在线段上,则,,
,向量在向量上投影长为,
而,则点Р到直线的距离
,当且仅当时取“=”,
所以点Р到直线的距离的最小值为.
故答案为:
考点二 点面距
【例2】 (2023·江苏常州)已知正方体的棱长为2,,分别为上底面和侧面的中心,则点到平面的距离为( )
A.B.C.D.
【答案】A
【解析】
如图,以为原点,所在直线为轴建立空间直角坐标系,易知,
设平面的法向量,则,令,解得,
故点到平面的距离为.
故选:A.
【一隅三反】
1. (2023·哈尔滨)在长方体中,,,则点到平面的距离等于_____.
【答案】
【解析】如图,以为原点,为轴,为轴,为轴,
建立空间直角坐标系,
则,,,,
,,,
设平面的法向量,
则,取,得,
点到平面的距离:.
故答案为:.
2. (2023·江苏)将边长为的正方形沿对角线折成直二面角,则点到平面的距离为___.
【答案】
【解析】记AC与BD的交点为O,图1中,由正方形性质可知,
所以在图2中,,所以,即
如图建立空间直角坐标系,易知
则
则
设为平面ABC的法向量,
则,取,得
所以点到平面的距离
故答案为:
3. (2023·福建福州)如图,在正四棱柱中,已知,,E,F分别为,上的点,且.
(1)求证:平面ACF:
(2)求点B到平面ACF的距离.
【答案】(1)证明见详解.(2).
【解析】(1)以为坐标原点,为轴,为轴,为轴建立空间直角坐标系,如下图所示:
则,设面的一个法向量为,,可得,即,不妨令则,平面.
(2),则点到平面的距离为.
考点三 线线距
【例3】 (2023·全国·高三专题练习)在长方体中,,,,则异面直线与之间的距离是( )
A.B.C.D.
【答案】D
【解析】如图所示,以为原点,所在直线为轴如图建立空间直角坐标系
则
设直线与的公垂线的方向向量为则
不妨令又
则异面直线与之间的距离故选:D
【一隅三反】
1. (2023·山东)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体中,,,,则异面直线与之间的距离是( )
A.B.C.D.
【答案】D
【解析】如图,以D为坐标原点建立空间直角坐标系,
则,则,,
设和的公垂线的方向向量,
则,即,令,则,
,.故选:D.
【点睛】
2. (2023·江苏)长方体中,,,为的中点,则异面直线与之间的距离是( )
A.B.C.D.
【答案】D
【解析】建立如图所示的空间直角坐标系,则,,,,,
,,
设与的公垂线的一个方向向量为,
则,取,得,,即,
又,所以异面直线与之间的距离为.故选:D.
3. (2023·全国·高三专题练习)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为1的正方体中,直线与之间的距离是( )
A.B.C.D.
【答案】B
【解析】
设为直线上任意一点, 过作,垂足为,可知此时到直线距离最短
设,,
则,
,
,,
即,
,即,
,
,
,
当时,取得最小值,
故直线与之间的距离是.
故选:B.
考点四 线面距
【例4】 (2023广西)如图,已知斜三棱柱在底面上的射影恰为的中点又知.
(1)求证:平面;
(2)求到平面的距离.
【答案】(1)证明见解析(2)
【解析】(1)证明:∵在底面上的射影为的中点,∴平面平面,∵,且平面平面,平面,∴平面,∵平面,∴,∵,且,平面,∴平面.
(2)解:取的中点,以为坐标原点,,,分别为轴,轴,轴建立空间直角坐标系,∵平面,平面,∴,∴四边形是菱形,∵是的中点,∴,∴,,,,∴,,设平面的法向量,则,,取,,到平面的距离.,平面,平面 平面,到平面的距离等于到平面的距离.
【一隅三反】
1. (2023·山西)如图,在正方体中,为的中点.
(1)证明:平面AD1E
(2)求直线到平面的距离;
【答案】(1)证明见解析(2)
【解析】(1),,四边形为平行四边形,,面,面,平面.
(2)如图建立空间直角坐标系,设正方体的棱长为,
则,,,,,平面,直线到平面的距离即为点到平面的距离,所以,,,设平面的一个法向量为,则,取,得,,直线到平面的距离为.
2. (2023·海南)如图,在正方体中,棱长为2,为的中点.
(1)求到平面的距离.
(2)若面,求.
【答案】(1)(2)
【解析】(1)如图,以A为坐标原点, 分别为x,y,z轴建立空间直角坐标系,
则 ,
因为正方体中,平面,
所以平面,则到平面的距离即为到平面的距离,
而 ,
设平面的法向量为 ,则 ,
即 ,令 ,则 ,
故,故到平面的距离 ,
即到平面的距离为;
(2) ,
由题意可得.
3. (2023·北京)图1是直角梯形,四边形是边长为2的菱形,并且,以为折痕将折起,使点到达的位置,且,如图2.
(1)求证:平面平面;
(2)在棱上是否存在点,使得到平面的距离为?若存在,求出直线与平面所成角的正弦值.
【答案】(1)详见解析;(2)存在点且为的中点;.
【解析】(1)证明:如图所示:
在图1中连接AC,交BE于O,
因为四边形是边长为2的菱形,并且,
所以,且,
在图2中,相交直线均与BE垂直,
所以是二面角的平面角,
因为,则,
所以平面平面;
(2)
由(1)分别以为x,y,z建立如图所示空间直角坐标系,
则,
所以,
设,
则,
设平面的一个法向量为,
则,即,取,
因为到平面的距离为,
所以,解得,
则,所以,
设直线与平面所成的角为,
所以直线与平面所成角的正弦值为:.
考点五 面面距
【例5】 (2023·全国·高三专题练习)已知正方体的棱长为a,则平面与平面的距离为( )
A.B.C.D.
【答案】D
【解析】由正方体的性质,∥,∥,,,
易得平面平面,
则两平面间的距离可转化为点B到平面的距离.
以D为坐标原点,DA,DC,所在的直线分别为x轴、y轴、z轴
建立空间直角坐标系,
则,,,,,
所以,,,.
连接,由,,且,可知平面,
得平面的一个法向量为,
则两平面间的距离.
故选:D
【一隅三反】
1. (2023·全国·高三专题练习)在棱长为的正方体中,则平面与平面之间的距离为
A.B.
C.D.
【答案】B
【解析】建立如图所示的直角坐标系,则,,,,
所以,,,
设平面的一个法向量,则,
即,解得,故,
显然平面平面,
所以平面与平面之间的距离.
2.(2022山西)两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是 ( )
A.B.C.D.
【答案】B
【解析】两平行平面 , 分别经过坐标原点 和点 ,,且两平面的一个法向量两平面间的距离,故选B.
3.(2022·青海西宁)底面为菱形的直棱柱中,分别为棱的中点.
(1)在图中作一个平面,使得,且平面.(不必给出证明过程,只要求作出与直棱柱的截面).
(2)若,求平面与平面的距离.
【答案】(1)见解析;(2).
【解析】
【详解】
(1)如图,取的中点,连接,则平面即为所求平面.
(2)如图,连接交于,
∵在直棱柱中,底面为菱形,
∴,
∴分别以为轴,为原点建立如图所示空间直角坐标系,
又∵所有棱长为2,,
∴,,,
∴,
∴,,
设是平面的一个法向量,则,即,
令得,,
∴点到平面的距离,
∴平面与平面的距离.
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.3 统计案例(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.3 统计案例(精讲)(基础版)(原卷版+解析版),共33页。试卷主要包含了线性回归方程,非线性回归方程,独立性检验等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版),共25页。试卷主要包含了裂项相消,错位相减,分组求和,倒序相加等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.3 利用递推公式求通项(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.3 利用递推公式求通项(精讲)(基础版)(原卷版+解析版),共22页。试卷主要包含了累加法,累乘法,公式法,构造等差数列,构造等比数列等内容,欢迎下载使用。












